Teoremas de conservación para una partícula

De Laplace

Contenido

1 Constantes de movimiento
- 1.1 Constantes dependientes del tiempo
2 Cantidad de movimiento
3 Momento cinético
- 3.1 Conservación parcial del momento cinético
4 Trabajo y energía cinética
- 4.1 Trabajo y potencia
- 4.2 Teorema de la fuerzas vivas
5 Energía mecánica
- 5.1 Energía potencial
- 5.2 Conservación de la energía mecánica
6 Ejemplos
- 6.1 Órbita de transferencia

1 Constantes de movimiento

Una constante de movimiento o integral primera es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una), cuyo valores constante en el tiempo, pese a que la posición y la velocidad si son variables en el tiempo

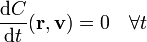
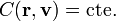
$\frac{\mathrm{d}C}{\mathrm{d}t}(\mathbf{r},\mathbf{v})=0\quad\forall t$ $\Rightarrow$ $C(\mathbf{r},\mathbf{v})=\mathrm{cte.}$

El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.

Se denominan también integrales primeras, porque estas cantidades suelen obtenerse integrando una vez las ecuaciones de movimiento.

El hallazgo de una constante de movimiento en un problema simplifica la solución de éste, ya que permite establecer relaciones entre las variables y limita el número de soluciones posibles.

El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posición y velocidad en cualquier instante)

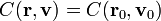
$C(\mathbf{r},\mathbf{v})=C(\mathbf{r}_0,\mathbf{v}_0)\,$

Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. Por ejemplo, en el movimiento planetario se conserva el llamado vector de Laplace-Runge-Lenz, que carece de interpretación sencilla.

1.1 Constantes dependientes del tiempo

Más en general, pueden encontrarse constantes de movimiento que además de la posición y velocidad, dependen del tiempo

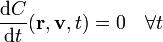
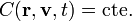
$\frac{\mathrm{d}C}{\mathrm{d}t}(\mathbf{r},\mathbf{v},t)=0\quad\forall t$ $\Rightarrow$ $C(\mathbf{r},\mathbf{v},t)=\mathrm{cte.}$

Su valor concreto lo da de nuevo la evaluación en un instante concreto

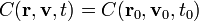
$C(\mathbf{r},\mathbf{v},t)=C(\mathbf{r}_0,\mathbf{v}_0,t_0)\,$

Puede parecer raro que se diga que una cantidad función del tiempo no depende del tiempo. Lo que se afirma es que aunque en la función puede aparecer la variable $t$ , el valor de la función es constante.

Por ejemplo, consideremos el caso de una partícula libre, para la cual F = 0

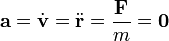
$\mathbf{a}=\dot{\mathbf{v}}=\ddot{\mathbf{r}}=\frac{\mathbf{F}}{m}=\mathbf{0}$

En este caso, la velocidad es una constante de movimiento

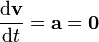
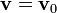
$\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=\mathbf{a}=\mathbf{0}$ $\Rightarrow$ $\mathbf{v}=\mathbf{v}_0\,$

Si ahora construimos la cantidad vectorial, función del tiempo,

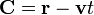
$\mathbf{C} = \mathbf{r}-\mathbf{v}t$

donde $\mathbf{r}$ y $\mathbf{v}$ son las velocidades instantáneas. ¿Cuánto vale su derivada respecto al tiempo?

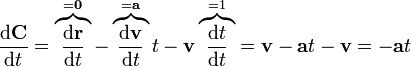
$\frac{\mathrm{d}\mathbf{C}}{\mathrm{d}t}=\overbrace{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}^{=\mathbf{0}}-\overbrace{\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}}^{=\mathbf{a}}t-\mathbf{v}\overbrace{\frac{\mathrm{d}t}{\mathrm{d}t}}^{=1} = \mathbf{v}-\mathbf{a}t-\mathbf{v}=-\mathbf{a}t$

Para una partícula libre la aceleración es nula, así que

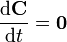
$\frac{\mathrm{d}\mathbf{C}}{\mathrm{d}t}=\mathbf{0}$

y por tanto 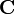$\mathbf{C}$ tiene siempre el mismo valor, aunque sea una función del tiempo. Hallamos este valor a partir de las condiciones iniciales.

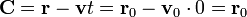
$\mathbf{C}=\mathbf{r}-\mathbf{v}t=\mathbf{r}_0-\mathbf{v}_0\cdot 0 = \mathbf{r}_0$

Y ahora, una vez que tenemos las dos constantes de movimiento, podemos depejar y escribir la solución

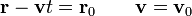
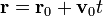
$\mathbf{r}-\mathbf{v}t= \mathbf{r}_0\qquad\mathbf{v}=\mathbf{v}_0$ $\Rightarrow$ $\mathbf{r}=\mathbf{r}_0+\mathbf{v}_0t$

Hemos llegado al resultado conocido de que una partícula libre describe un movimiento rectilíneo y uniforme siguiendo un camino más complicado que el habitual. Sin embargo, en muchos problemas más complicados, el uso de integrales primeras es el método más sencillo e intuitivo.

2 Cantidad de movimiento

Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad

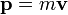
$\mathbf{p}=m\mathbf{v}\,$

La segunda ley de Newton tal como la formuló el propio Newton establece que la derivada respecto al tiempo de la cantidad de movimiento es la resultante de las fuerzas aplicadas sobre la partícula

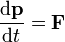
$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\mathbf{F}$

Esta ecuación, para el caso de masa constante, se reduce a la más familiar versión 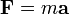$\mathbf{F}=m\mathbf{a}$ .

De esta expresión es inmediato que:

“La cantidad de movimiento de una partícula permanece constante cuando la fuerza es nula durante un intervalo de tiempo”

Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.

En ocasiones, no nos interesa tanto establecer la constancia de la cantidad de movimiento, sino saber cuánto varía. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 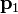$\mathbf{p}_1$ . Entonces es sometida a una fuerza 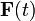$\mathbf{F}(t)$ durante un intervalo entre $t 1$ y $t 2$ (por ejemplo, durante una colisión, a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 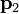$\mathbf{p}_2$ . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos

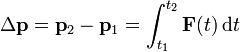
$\Delta \mathbf{p}=\mathbf{p}_2-\mathbf{p}_1 = \int_{t_1}^{t_2}\mathbf{F}(t)\,\mathrm{d}t$

Esta integral de la fuerza sobre un intervalo recibe el nombre de impulso, por tanto la igualdad anterior establece que “``el incremento de la cantidad de movimiento es igual al impulso recibido”. Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.

3 Momento cinético

Artículo completo: Momento cinético de una partícula

Se define el momento cinético (o momento angular)de una partícula respecto a un punto O como la cantidad

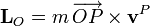
$\mathbf{L}_O=m\,\overrightarrow{OP}\times\mathbf{v}^P$

o, más sencillamente

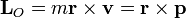
$\mathbf{L}_O = m \mathbf{r}\times\mathbf{v}=\mathbf{r}\times\mathbf{p}\,$

donde hay que entender que el vector de posición se mide respecto al punto O. Si queremos medir el momento angular respecto a un punto B el momento cinético cambia correspondientemente

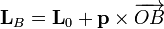
$\mathbf{L}_{B}=\mathbf{L}_0+\mathbf{p}\times\overrightarrow{OB}$

De la definición de momento cinético resulta proporcionalidad a la velocidad areolar

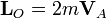
$\mathbf{L}_O=2m\mathbf{V}_A\,$

y por tanto la constancia del momento cinético equivale a la de la velocidad areolar.

Derivando el momento cinético respecto al tiempo

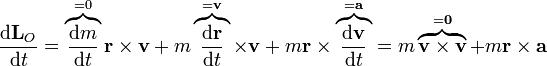
$\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}=\overbrace{\frac{\mathrm{d}m}{\mathrm{d}t}}^{=0}\mathbf{r}\times\mathbf{v}+m\overbrace{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}^{=\mathbf{v}}\times\mathbf{v}+m\mathbf{r}\times\overbrace{\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}}^{=\mathbf{a}}=m\overbrace{\mathbf{v}\times\mathbf{v}}^{=\mathbf{0}}+m\mathbf{r}\times\mathbf{a}$

El producto 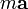$m\mathbf{a}$ es la resultante de las fuerzas que actúan sobre la partícula, por tanto

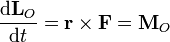
$\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}=\mathbf{r}\times\mathbf{F}=\mathbf{M}_O$

Por tanto, la derivada respecto al tiempo del momento cinético respecto a un punto es igual al momento, respecto al mismo punto, de las fuerza neta que actúa sobre dicha partícula. Esto ocurrirá cuando la fuerza sea nula o cuando sea paralela al vector de posición (fuerza central). Por ello, podemos enunciar el teorema de conservación en la forma

“Si la fuerza neta que actúa sobre una partícula P es nula o es central con centro en un punto fijo O durante un cierto intervalo de tiempo, el momento cinético de la partícula respecto al punto O se mantiene constante durante dicho intervalo.”

Entre las fuerzas centrales que verifican la ley de conservación del momento cinético respecto al centro de fuerzas están:

La ley de Hooke
La ley de la Gravitación Universal
La ley de Coulomb

3.1 Conservación parcial del momento cinético

Existen ocasiones, como en el caso del peso mencionado anteriormente, en que el momento cinético no se conserva. Sin embargo, incluso en esos casos es a menudo obtener una ley de conservación más restringida.

Para ello, tenemos en cuenta que el momento cinético es un vector y posee tres componentes. Puede ocurrir que aunque el vector como tal no sea constante, una de sus componentes sí lo sea. Sea 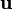$\mathbf{u}$ un vector unitario fijo. La componente del momento angular según la dirección de 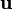$\mathbf{u}$ es

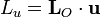
$L_{u}=\mathbf{L}_O\cdot\mathbf{u}\,$

Derivando aquí respecto al tiempo

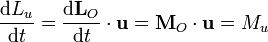
$\frac{\mathrm{d}L_u}{\mathrm{d}t}=\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}\cdot\mathbf{u}=\mathbf{M}_O\cdot\mathbf{u}=M_u$

Si se anula la componente en la dirección de 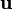$\mathbf{u}$ del momento de las fuerzas aplicadas, la componente del momento cinético en dicha dirección permanece constante.

4 Trabajo y energía cinética

4.1 Trabajo y potencia

Se define el trabajo elemental realizado por una fuerza 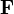$\mathbf{F}$ sobre una partícula que realiza un desplazamiento diferencial 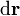$\mathrm{d}\mathbf{r}$ como la cantidad escalar

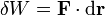
$\delta W=\mathbf{F}\cdot\mathrm{d}\mathbf{r}$

A partir de aquí obtenemos el trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C como la suma de los trabajos elementales a lo largo de dicha curva

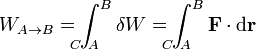
$W_{A\to B} = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \delta W = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}$

Igualmente, se define la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo $d t$ , dividido por dicho intervalo

$P = \frac{\delta W}{\mathrm{d}t}=\mathbf{F}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}=\mathbf{F}\cdot\mathbf{v}$

4.2 Teorema de la fuerzas vivas

Artículo completo: Teorema de las fuerzas vivas

Aplicando la segunda ley de Newton la potencia desarrollada por una fuerza puede escribirse como la derivada respecto al tiempo de la energía cinética

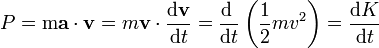
$P = \mathrm{m}\mathbf{a}\cdot\mathbf{v}= m\mathbf{v}\cdot\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{1}{2}mv^2\right)=\frac{\mathrm{d}K}{\mathrm{d}t}$

siendo K la energía cinética de la partícula

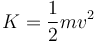
$K = \frac{1}{2}mv^2$

(donde 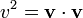$v^2 = \mathbf{v}\cdot\mathbf{v}$ es el módulo de la velocidad, o celeridad, al cuadrado).

Integrando respecto al tiempo obtenemos el teorema de las fuerzas vivas (o teorema trabajo-energía cinética):

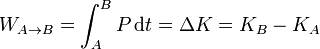
$W_{A\to B}=\int_A^B P\,\mathrm{d}t=\Delta K = K_B-K_A$

En palabras:

“El trabajo realizado sobre una partícula entre dos puntos equivale al incremento de la energía cinética de dicha partícula.”

El trabajo realizado no tiene por qué ser necesariamente positivo. Si la partícula se ve frenada, su energía cinética disminuye y el trabajo resultante es negativo.

Este teorema implica, entre otras resultados, que una partícula sometida a una fuerza puramente normal en todo momento (como es la fuerza magnética 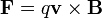$\mathbf{F}=q\mathbf{v}\times\mathbf{B}$ ) mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante).

5 Energía mecánica

5.1 Energía potencial

Artículo completo: Energía potencial

El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos.

Existe una clase de fuerzas, denominadas fuerzas conservativas, para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro

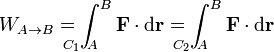
$W_{A\to B}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_1\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_2\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}$

Esto permite definir una función denominada energía potencial como el trabajo, cambiado de signo, para ir desde un punto fijo (el origen de potencial) hasta un punto fijo

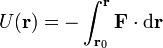
$U(\mathbf{r})=-\int_{\mathbf{r}_0}^\mathbf{r} \mathbf{F}\cdot\mathrm{d}\mathbf{r}$

Entre los casos importantes de fuerzas conservativas tenemos:

El peso, para el cual, si el origen de potencial es la superficie terrestre y $z$ la altura sobre ella:

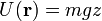
$U(\mathbf{r}) = mg z\,$

Más en general la fuerza gravitatoria producida por un cuerpo fijo sobre otro, tomando como origen de potencial el infinito, tiene una energía potencial

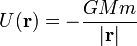
$U(\mathbf{r}) = -\frac{GMm}{|\mathbf{r}|}\,$

El oscilador armónico, que cumple, tomando el origen de potencial en el punto de equilibrio

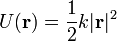
$U(\mathbf{r}) = \frac{1}{2}k|\mathbf{r}|^2\,$

Conocida la energía potencial, puede hallarse la fuerza calculando su gradiente:

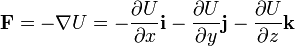
$\mathbf{F}=-\nabla U = -\frac{\partial U}{\partial x}\mathbf{i}-\frac{\partial U}{\partial y}\mathbf{j}-\frac{\partial U}{\partial z}\mathbf{k}$

que en el caso de una función dependiente de una sola coordenada se reduce a una derivada ordinaria.

5.2 Conservación de la energía mecánica

Artículo completo: Teorema de conservación de la energía mecánica

Cuando existe una energía potencial de la cual deriva la fuerza que actúa sobre una partícula se cumple la siguiente identidad

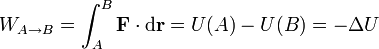
$W_{A\to B} = \int_A^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}=U(A)-U(B) = -\Delta U$

esto es, el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial.

Combinando este teorema con el de las fuerzas vivas obtenemos

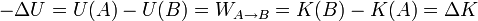
$-\Delta U = U(A) - U(B) = W_{A\to B} = K(B) - K(A) = \Delta K$

esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa). Reagrupando términos y definiendo la energía mecánica de la partícula como la suma de su energía cinética más la potencial obtenemos

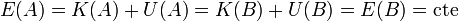
$E(A) = K(A) + U(A) = K(B) + U(B) = E(B) = \mathrm{cte}\,$

lo que se conoce como teorema de conservación de la energía mecánica:

“En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.”

Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como fuerzas disipativas.

Si sobre una partícula actúan tanto fuerzas conservativas como no conservativas, las consideramos por separado. Aplicando el teorema de las fuerzas vivas

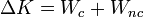
$\Delta K = W_c+W_{nc}\,$

El trabajo de las fuerzas conservativas es igual a la disminución de su energía potencial

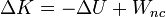
$\Delta K = -\Delta U + W_{nc}\,$

Agrupando términos resulta que el incremento de la energía mecánica es igual al trabajo de las fuerzas no conservativas

Δ E = W n c

En el caso particular de una fuerza de rozamiento, este trabajo es negativo y la energía mecánica disminuye como consecuencia de la fricción.

Si en lugar de considerar un incremento finito, calculamos la derivada respecto al tiempo obtenemos

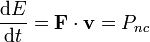
$\frac{\mathrm{d}E}{\mathrm{d}t}=\mathbf{F}\cdot\mathbf{v}=P_{nc}$

esto es, la derivada de la energía mecánica es la potencia desarrollada por las fuerzas no conservativas.

6 Ejemplos

6.1 Órbita de transferencia

Artículo completo: Órbita de transferencia

Teoremas de conservación para una partícula

De Laplace

Contenido

1 Constantes de movimiento

1.1 Constantes dependientes del tiempo

2 Cantidad de movimiento

3 Momento cinético

3.1 Conservación parcial del momento cinético

4 Trabajo y energía cinética

4.1 Trabajo y potencia

4.2 Teorema de la fuerzas vivas

5 Energía mecánica

5.1 Energía potencial

5.2 Conservación de la energía mecánica

6 Ejemplos

6.1 Órbita de transferencia

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES