Teorema de conservación de la energía mecánica
De Laplace
Contenido |
1 Teorema de las fuerzas vivas
El trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C es igual a la suma de los trabajos elementales a lo largo de dicha curva
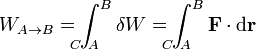
Se define asimismo la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo dt, dividido por dicho intervalo
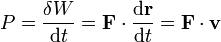
Aplicando la segunda ley de Newton la potencia desarrollada por una fuerza puede escribirse como la derivada respecto al tiempo de la energía cinética
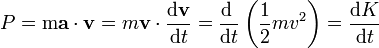
siendo K la energía cinética de la partícula
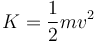
(donde 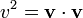 es el módulo de la velocidad, o celeridad, al cuadrado).
es el módulo de la velocidad, o celeridad, al cuadrado).
Integrando respecto al tiempo obtenemos el teorema de las fuerzas vivas (o teorema trabajo-energía cinética):
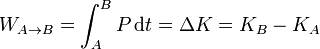
En palabras:
- “El trabajo realizado sobre una partícula entre dos puntos equivale al incremento de la energía cinética de dicha partícula.”
El trabajo realizado no tiene por qué ser necesariamente positivo. Si la partícula se ve frenada, su energía cinética disminuye y el trabajo resultante es negativo.
2 Fuerzas conservativas
El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos.
Existe una clase de fuerzas, denominadas fuerzas conservativas, para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro
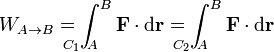
para una fuerza conservativa, por tanto, podemos omitir la indicación de la curva y escribir simplemente
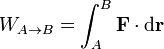
donde la integral se calcula por un camino arbitrario.
Esto nos permite definir la energía potencial de la cual deriva la fuerza conservativa como
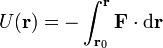
donde  es un punto fijo, conocido como origen de potencial para el cual la energía potencial es nula.
es un punto fijo, conocido como origen de potencial para el cual la energía potencial es nula.
Para el caso de fuerzas conservativas puede enunciarse un teorema complementario al teorema de las fuerzas vivas.
A la hora de calcular el trabajo realizado por una fuerza conservativa para ir de un punto A a uno B podemos elegir un camino que pase por el origen de potencial. De esta forma, podemos expresar el trabajo como diferencia entre dos energías potenciales

esto es:
- “El trabajo realizado por una fuerza conservativa es igual al decremento de su energía potencial.”
Combinando este teorema con el de las fuerzas vivas se llega al teorema de conservación de la energía mecánica.
Si consideramos la variación instantánea de la energía potencial llegamos a la siguiente relación para fuerzas conservativas
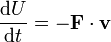
3 Teorema de conservación de la energía mecánica
Combinando el teorema de las fuerzas vivas con el de la energía potencial obtenemos que, cuando todas las fuerzas son conservativas
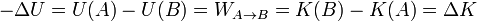
esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa).
Reagrupando términos y definiendo la energía mecánica de la partícula como la suma de su energía cinética más la potencial obtenemos
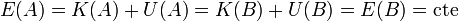
lo que se conoce como teorema de conservación de la energía mecánica:
- “En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.”
Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como fuerzas disipativas.
La constancia de la energía mecánica puede expresarse en forma de derivada temporal
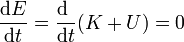
4 Ejemplos
4.1 Caída de un cuerpo
Supongamos un cuerpo que cae verticalmente desde una cierta altura h. Nos preguntamos por su velocidad al llegar al suelo, si parte del reposo y no hay rozamiento.
Puesto que la única fuerza que actúa es el peso y ésta es conservativa, la energía mecánica es constante, por lo que
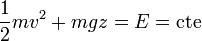
Igualando su valor inicial (en donde es nula la energía cinética) y el suelo (donde lo es la potencial) nos queda
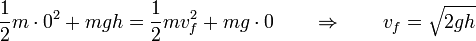
Si la masa no cae verticalmente, sino que desliza por un plano inclinado o es obligada a moverse por una curva o superficie sin rozamiento, el resultado es exactamente el mismo, ya que la fuerza de reacción vincular debida a un vínculo liso es normal a la curva o superficie que la produce. Por tanto, estas fuerzas de reacción ni quitan ni añaden nada a la energía mecánica.
4.2 Oscilador armónico
En el caso del oscilador armónico unidimensional la solución general para la elongación y la velocidad puede escribirse en la forma
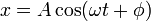
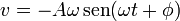
A partir de aquí obtenemos la energía cinética
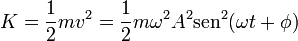
y la potencial
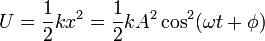
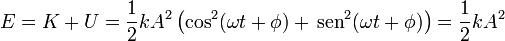
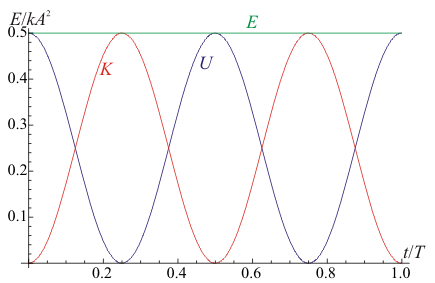
Resulta una energía mecánica, por supuesto constante, proporcional al cuadrado de la amplitud. Representando las energías cinética, potencial y mecánica frente al tiempo para el oscilador armónico vemos que las dos primeras son funciones oscilantes, mientras que la energía mecánica, suma de las dos, permanece constante. Desde el punto de vista energético, un oscilador armónico transforma alternativamente energía cinética en potencial y viceversa.
La frecuencia con la que oscila cada energía es el doble de la frecuencia con la que oscila la elongación. La energía potencial pasa de un máximo, cuando la elongación vale + A a valer 0, cuando la partícula pasa por la posición de equilibrio, y de ahí vuelve aun máximo cuando x = − A.
4.3 Velocidad de escape
La velocidad de escape se define como la mínima velocidad que es preciso comunicar a un cuerpo ligero para salir del campo gravitatorio de otro masivo.
Esta velocidad mínima es la que permite llegar al infinito con velocidad nula. Una velocidad menor no permitiría salir del “pozo” de energía potencial gravitatoria.
La energía mecánica de una partícula en un campo gravitatorio es
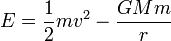
Imponiendo que 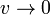 cuando
cuando 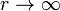 queda
queda
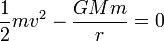

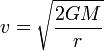
Aquí r es la distancia de partida. En el caso de un cohete que parte de la superficie terrestre r = RT. El valor de GM lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre
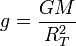

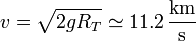
Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol.
5 Presencia de fuerzas no conservativas
Si sobre una partícula actúan tanto fuerzas conservativas como no conservativas, las consideramos por separado
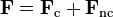

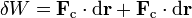
Integrando y aplicando el teorema de las fuerzas vivas
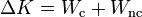
El trabajo de las fuerzas conservativas es igual a la disminución de su energía potencial
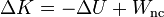
Agrupando términos resulta que el incremento de la energía mecánica es igual al trabajo de las fuerzas no conservativas
En el caso particular de una fuerza de rozamiento, este trabajo es negativo y la energía mecánica disminuye como consecuencia de la fricción.
Si en lugar de considerar un incremento finito, calculamos la derivada respecto al tiempo obtenemos
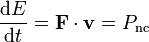
esto es, la derivada de la energía mecánica es la potencia desarrollada por las fuerzas no conservativas.