Cilindro imanado en dirección acimutal
De Laplace
(Nueva página: Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, [[Campos_vectoriales_e...) |
|||
| Línea 1: | Línea 1: | ||
| + | __TOC__ | ||
| + | ==Enunciado== | ||
Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, [[Campos_vectoriales_en_diferentes_sistemas#Quinto_campo|expresable en cilíndricas o cartesianas]] como | Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, [[Campos_vectoriales_en_diferentes_sistemas#Quinto_campo|expresable en cilíndricas o cartesianas]] como | ||
<center><math>\mathbf{M}=C\rho\mathbf{u}_\varphi = C(-y\mathbf{u}_x+x\mathbf{u}_y)</math></center> | <center><math>\mathbf{M}=C\rho\mathbf{u}_\varphi = C(-y\mathbf{u}_x+x\mathbf{u}_y)</math></center> | ||
| - | Supongamos un cilindro de radio <math>R</math> y longitud <math>L</math> imanado de esta forma. Las corrientes de magnetización son nulas en el exterior del cilindro, mientras que en el interior puede [[Cálculo_de_divergencias_y_rotacionales#Campo_B|hallarse | + | Supongamos un cilindro de radio <math>R</math> y longitud <math>L</math> imanado de esta forma. |
| + | |||
| + | # Calcule las corrientes de imanación equivalentes a esta magnetización. | ||
| + | # Halle las cargas magnéticas equivalentes a esta barra. | ||
| + | # Determine los campos magnético <math>\mathbf{H}</math> y <math>\mathbf{B}</math> en este sistema. | ||
| + | |||
| + | ==Corrientes de magnetización== | ||
| + | ===Volumétricas=== | ||
| + | Las [[corrientes de magnetización]] en el volumen se calculan como | ||
| + | |||
| + | <center><math>\mathbf{J}_m = \nabla\times\mathbf{M}\,</math></center> | ||
| + | |||
| + | Estas corrientes son nulas son nulas en el exterior del cilindro, mientras que en el interior puede [[Cálculo_de_divergencias_y_rotacionales#Campo_B|hallarse el rotacional]] de la imanación | ||
<center><math>\mathbf{J}_m = \nabla\times\mathbf{M}=2C\mathbf{u}_z</math></center> | <center><math>\mathbf{J}_m = \nabla\times\mathbf{M}=2C\mathbf{u}_z</math></center> | ||
| - | + | Resultan corrientes que suben axialmente por el cilindro. | |
| + | |||
| + | ===Superficiales=== | ||
| + | Las corrientes de magnetización en una interfaz entre dos regiones tienen la forma general | ||
| + | |||
| + | <center><math>\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]\,</math></center> | ||
| + | |||
| + | que, para el caso de que una de las dos regiones sea el vacío, se reduce a | ||
| + | |||
| + | <center><math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}\,</math></center> | ||
| + | |||
| + | siendo <math>\mathbf{n}</math> la normal exterior al volumen imanado. En nuestro caso, tenemos | ||
* En la base superior <math>\mathbf{n}=+\mathbf{u}_z</math> y | * En la base superior <math>\mathbf{n}=+\mathbf{u}_z</math> y | ||
| Línea 22: | Línea 47: | ||
Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación. | Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación. | ||
| + | |||
| + | ==Cargas magnéticas== | ||
| + | ==Campos magnéticos== | ||
[[Categoría:Problemas de materiales magnéticos]] | [[Categoría:Problemas de materiales magnéticos]] | ||
Revisión de 13:01 3 abr 2009
Contenido |
1 Enunciado
Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, expresable en cilíndricas o cartesianas como
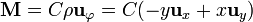
Supongamos un cilindro de radio R y longitud L imanado de esta forma.
- Calcule las corrientes de imanación equivalentes a esta magnetización.
- Halle las cargas magnéticas equivalentes a esta barra.
- Determine los campos magnético
 y
y  en este sistema.
en este sistema.
2 Corrientes de magnetización
2.1 Volumétricas
Las corrientes de magnetización en el volumen se calculan como

Estas corrientes son nulas son nulas en el exterior del cilindro, mientras que en el interior puede hallarse el rotacional de la imanación
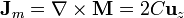
Resultan corrientes que suben axialmente por el cilindro.
2.2 Superficiales
Las corrientes de magnetización en una interfaz entre dos regiones tienen la forma general
![\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]\,](/wiki/images/math/e/5/6/e5696e953c72cfdd30df07674308cb82.png)
que, para el caso de que una de las dos regiones sea el vacío, se reduce a
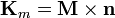
siendo  la normal exterior al volumen imanado. En nuestro caso, tenemos
la normal exterior al volumen imanado. En nuestro caso, tenemos
- En la base superior
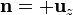 y
y
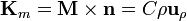
- En la base inferior
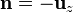 y
y

- En la cara lateral
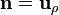
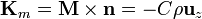
Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación.





