Sistemas de partículas (CMR)
De Laplace
| Línea 40: | Línea 40: | ||
*[[Energía de un sistema de partículas (CMR)|Energía]] | *[[Energía de un sistema de partículas (CMR)|Energía]] | ||
| - | [[Categoría: | + | [[Categoría:Mecánica de la partículas y de los sistemas (CMR)]] |
Revisión de 08:30 1 oct 2016
Definición de sistema de partículas
En mecánica consideramos un sistema de partículas como un conjunto de N partículas que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas.
El número de partículas que forman un sistema puede ser muy variado e ir desde 2 (por ejemplo, al estudiar un átomo de hidrógeno), hasta cantidades gigantescas (por ejemplo, en 1 l de agua hay del orden de 1024 partículas).
Cuando el número de partículas es reducido se puede abordar el problema dinámico analizando cada una por separado. Cuando es elevado, es preciso recurrir a promedios y descripciones colectivas (como la mecánica estadística, la elasticidad o la mecánica de fluidos).
Los sistemas se clasifican en abiertos o cerrados. Un sistema cerrado es aquél en el que no entra ni salen partículas del sistema. Por tanto, su masa permanece constante. Un sistema abierto es aquel que permite el paso de partículas (y por tanto masa) a través de los límites del sistema. Aquí consideraremos solo sistemas cerrados.
Entre las fuerzas internas en un sistema estarían por ejemplo, las fuerzas eléctricas de atracción entre las cargas de un sistema de protones y electrones, o la atracción gravitatoria entre las estrellas de una galaxia. Entre las fuerzas externas figura, por ejemplo, el peso de un sistema de partículas, originado por la atracción de un cuerpo externo como la Tierra.
Cada una de las partículas del sistema posee una masa propia, mi, siendo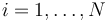 
un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición 
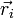y una velocidad 
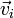. Esta posición y esta velocidad evolucionan de acuerdo con las leyes de la dinámica
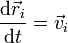
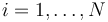
siendo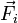 
la resultante de las fuerzas que actúan sobre la partícula i. Esta resultante se compone de las fuerzas internas que cada una de las demás partículas del sistema ejerce sobre i, más la resultante de las fuerzas externas (causadas por un agente externo al sistema) aplicadas sobre ella
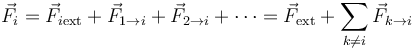
Suponemos que las interacciones entre las partículas obedecen la 3ª ley de Newton
o, lo que es lo mismo
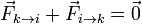
En la mayoría de los casos se cumplirá además que la fuerza que la partícula k ejerce sobre la i (y por tanto la que la i ejerce sobre la k) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector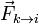 
es paralelo a la posición relativa 
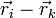, esto es, si
Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición
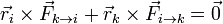
El estudio de la evolución de las partículas que coimponen un sistema puede ser extraordinariamente complejo cuando hay más de 2 e imposible cuando hay millones, como en un fluido. Por ello, se consideran propiedades colectivas y se analiza su evolución y los casos en que son constantes.
