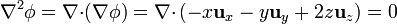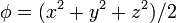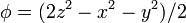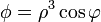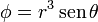Cálculo de laplacianos
De Laplace
(Diferencias entre revisiones)
(→Primer campo) |
(→Segundo campo) |
||
| Línea 21: | Línea 21: | ||
===Segundo campo=== | ===Segundo campo=== | ||
| + | Para el segundo campo, de nuevo calculamos su gradiente en [[cálculo de gradientes|un problema]] y la divergencia de éste en [[cálculo de divergencias y rotacionales|otro]], donde se ve que | ||
| + | |||
| + | <center> | ||
| + | <math>\nabla^2\phi = \nabla{\cdot}(\nabla\phi) = | ||
| + | \nabla{\cdot}\left(-x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\right)= 0</math></center> | ||
| + | |||
===Tercer campo=== | ===Tercer campo=== | ||
===Cuarto campo=== | ===Cuarto campo=== | ||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
Revisión de 15:24 24 sep 2008
Contenido |
1 Enunciado
Calcule el laplaciano de los campos escalares
empleando coordenadas cartesianas, cilíndricas y esféricas.
2 Solución
2.1 Primer campo
El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de cálculo de gradientes que su gradiente vale
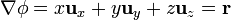
Hallar el laplaciano de 
equivale a calcular la divergencia del vector de posición. Pero este cálculo ya se hace en el problema de cálculo de divergencias y rotacionales. Allí se ve que, independientemente del sistema empleado para calcularla
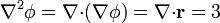
2.2 Segundo campo
Para el segundo campo, de nuevo calculamos su gradiente en un problema y la divergencia de éste en otro, donde se ve que
