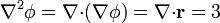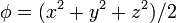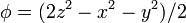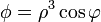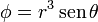Cálculo de laplacianos
De Laplace
(Diferencias entre revisiones)
(→Primer campo) |
(→Primer campo) |
||
| Línea 12: | Línea 12: | ||
==Solución== | ==Solución== | ||
===Primer campo=== | ===Primer campo=== | ||
| - | El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de [[cálculo de gradientes]] que su | + | El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de [[cálculo de gradientes#Primer campo]] que su |
gradiente vale | gradiente vale | ||
Revisión de 14:59 24 sep 2008
Contenido |
1 Enunciado
Calcule el laplaciano de los campos escalares
empleando coordenadas cartesianas, cilíndricas y esféricas.
2 Solución
2.1 Primer campo
El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de cálculo de gradientes#Primer campo que su gradiente vale
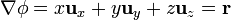
Hallar el laplaciano de 
equivale a calcular la divergencia del vector de posición. Pero este cálculo ya se hace en el problema de cálculo de divergencias y rotacionales. Allí se ve que, independientemente del sistema empleado para calcularla
