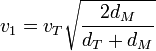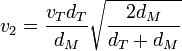Órbita de transferencia
De Laplace
(→Velocidad inicial y final) |
(→Velocidad inicial y final) |
||
| Línea 41: | Línea 41: | ||
<center><math>\frac{L_O}{m}=\sqrt{\frac{2GMd_Td_M}{d_T+d_M}}</math></center> | <center><math>\frac{L_O}{m}=\sqrt{\frac{2GMd_Td_M}{d_T+d_M}}</math></center> | ||
| + | |||
| + | Esto nos da las velocidades inicial y final | ||
| + | |||
| + | <center><math>v_1 = \frac{L_O}{md_T}=\sqrt{\frac{2GMd_M}{d_T(d_T+d_M)}}</math>{{qquad}}{{qquad}}<math>v_2 = \frac{L_O}{md_M}=\sqrt{\frac{2GMd_T}{d_M(d_T+d_M)}}</math></center> | ||
| + | |||
| + | Estas velocidades dependen de la constante <math>GM</math>, igual al producto de la constante de Gravitación Universal por la masa del objeto masivo, en este caso. Podemos obtener el valor de esta constante, observando que si la Tierra se mueve en una órbita circular, la fuerza gravitatoria es puramente normal y por tanto | ||
| + | |||
| + | <center><math>\frac{v_T^2}{d_T}=\frac{GM}{d_T^2}</math>{{tose}}<math>GM=v_T^2d_T</math></center> | ||
| + | |||
| + | A su vez, la velocidad de la Tierra observando que conocemos la distancia que recorre en un año. Sustituyendo el valor de la constante | ||
| + | |||
| + | <center><math>v_1 = v_T \sqrt{\frac{2d_M}{d_T+d_M}}</math>{{qquad}}<math>v_2=\frac{v_Td_T}{d_M}\sqrt{\frac{2d_M}{d_T+d_M}}</math></center> | ||
==Impulso== | ==Impulso== | ||
[[Categoría:Introducción a la dinámica]] | [[Categoría:Introducción a la dinámica]] | ||
Revisión de 16:55 17 feb 2010
Contenido |
1 Definición
Una órbita de transferencia es aquella que debe seguir un satélite para desplazarse desde una órbita circular de un cierto radio a una de un radio diferente. Por ejemplo, si interesa lanzar un satélite a Marte, dicha nave debe salir desde la órbita terrestre (a 1 UA del Sol) y llegar hasta la órbita marciana (a 1.66 UA). El camino que recorre es la órbita de transferencia.
2 Órbita de transferencia de Hohmann
La órbita que requiere un menor impulso inicial es aquella que hace un mayor uso del movimiento que el Sol imprime a la nave. Esto se consigue con la llamada “órbita de transferencia de Hohmann” (en honor a Walter Hohmann). En esta órbita la nave describe media elipse con el Sol en uno de sus focos, estando uno de los vértices en la posición inicial en la Tierra y el opuesto en la posición final en Marte.
En lo que sigue analizaremos esta órbita, calculando la velocidad inicial que debe comunicarse y la velocidad a la llegada, así como otros parámetros de interés.
3 Velocidad inicial y final
La clave para determinar las velocidades en los puntos iniciales es usar los teoremas de conservación para una partícula. La fuerza gravitatoria es una fuerza central, por lo que conserva el momento cinético del satélite, medido respecto al Sol
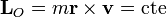
También es una fuerza conservativa, por lo que también se conserva la energía mecánica
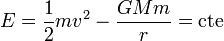
Aplicamos estas dos leyes a los puntos inicial y final de la órbita de transferencia. Por tratarse de vértices de la elipse, en los dos la velocidad es perpendicular al vector de posición, por lo que la única componente del momento cinético es
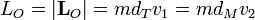
Igualando también las energías mecánicas inicial y final
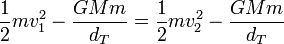
Esto nos da un sistema de dos ecuaciones con dos incógnitas, que podemos resolver de forma sencilla. De la conservación del momento cinético obtenemos
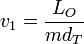
Sustituyendo en la ley de conservación de la energía obtenemos una ecuación para el momento cinético
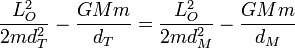
Agrupando términos
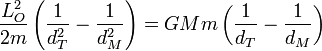
Simplificando y despejando
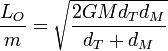
Esto nos da las velocidades inicial y final
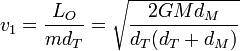
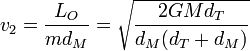
Estas velocidades dependen de la constante GM, igual al producto de la constante de Gravitación Universal por la masa del objeto masivo, en este caso. Podemos obtener el valor de esta constante, observando que si la Tierra se mueve en una órbita circular, la fuerza gravitatoria es puramente normal y por tanto
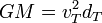
A su vez, la velocidad de la Tierra observando que conocemos la distancia que recorre en un año. Sustituyendo el valor de la constante
