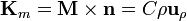Entrar Página Discusión Historial Go to the site toolbox

Corrientes de magnetización

De Laplace

(Diferencias entre revisiones)
(→Imán esférico)
(→Imán esférico)
Línea 32: Línea 32:
Por tanto, un imán cilíndrico es equivalente a un solenoide cilíndrico.
Por tanto, un imán cilíndrico es equivalente a un solenoide cilíndrico.
-
===Imán esférico===
+
===Barra imanada en dirección acimutal===
-
{{ac|Imán esférico}}
+
Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, [[Campos_vectoriales_en_diferentes_sistemas#Quinto_campo|expresable en cilíndricas o cartesianas]] como
-
En el caso de una esfera imanada uniformente, con magnetización <math>\mathbf{M}_0=M_0\mathbf{u}_z</math> la densidad de corriente de volumen es cero en el exterior de la esfera, en la cual la magnetización es nula. También lo es en el interior, ya que en él la magnetización es uniforme
+
-
<center><math>\mathbf{J}_m = \begin{cases}\nabla\times \mathbf{M}_0 = \mathbf{0} & r<R \\\nabla\times\mathbf{0} = \mathbf{0} & r> R\end{cases}</math></center>
+
<center><math>\mathbf{M}=C\rho\mathbf{u}_\varphi = C(-y\mathbf{u}_x+x\mathbf{u}_y)</math></center>
-
Las corrientes superficiales no son nulas, ya que tenemos una discontinuidad en la magnetización. Empleando coordenadas esféricas
+
Supongamos un cilindro de radio <math>R</math> y longitud <math>L</math> imanado de esta forma. Las corrientes de magnetización son nulas en el exterior del cilindro, mientras que en el interior puede [[Cálculo_de_divergencias_y_rotacionales#Campo_B|hallarse su rotacional]]
-
<center><math>\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]=\mathbf{u}_{r}\times(\mathbf{0}-M_0\mathbf{u}_{z})=M_0\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi}</math></center>
+
<center><math>\mathbf{J}_m = \nabla\times\mathbf{M}=2C\mathbf{u}_z</math></center>
 +
 
 +
Para las corrientes superficiales tenemos
 +
 
 +
* En la base superior <math>\mathbf{n}=+\mathbf{u}_z</math> y
 +
 
 +
<center><math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= C\rho\mathbf{u}_\rho\,</math></center>
 +
 
 +
* En la base inferior <math>\mathbf{n}=-\mathbf{u}_z</math> y
 +
 
 +
<center><math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= C\rho\mathbf{u}_\rho\,</math></center>
-
Estas corrientes rodean la esfera perpendicularmente a la magnetización.
 
[[Categoría:Materiales magnéticos]]
[[Categoría:Materiales magnéticos]]

Revisión de 12:50 3 abr 2009

Contenido

1 Definición

1.1 Transformación del potencial vector

1.2 Definición de las corrientes

1.2.1 Volumétricas

1.2.2 Superficiales

2 Interpretación física

3 Ejemplos

3.1 Imán cilíndrico

Artículo completo: Imán cilíndrico

Supongamos un cilindro de radio R y longitud L imanado axialmente con una magnetización uniforme 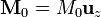\mathbf{M}_0=M_0\mathbf{u}_z. Para este imán

  • Las corrientes volumétricas de magnetización son nulas:
  • En el interior, por ser uniforme la imanación
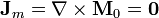
\mathbf{J}_m=\nabla\times\mathbf{M}_0=\mathbf{0}
  • En el exterior, por no haber magnetización
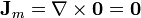
\mathbf{J}_m=\nabla\times\mathbf{0}=\mathbf{0}
  • Para las corrientes superficiales debemos distinguir entre las bases y la cara lateral
  • En las bases se anulan, por ser paralelos el vector normal y la imanación
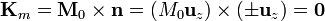
\mathbf{K}_m=\mathbf{M}_0\times\mathbf{n}=(M_0\mathbf{u}_z)\times(\pm\mathbf{u}_z)=\mathbf{0}
  • En la cara lateral resulta una corriente acimutal
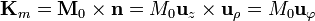
\mathbf{K}_m=\mathbf{M}_0\times\mathbf{n}=M_0\mathbf{u}_{z}\times\mathbf{u}_{\rho}=M_0\mathbf{u}_{\varphi}

Por tanto, un imán cilíndrico es equivalente a un solenoide cilíndrico.

3.2 Barra imanada en dirección acimutal

Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, expresable en cilíndricas o cartesianas como

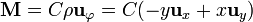
\mathbf{M}=C\rho\mathbf{u}_\varphi = C(-y\mathbf{u}_x+x\mathbf{u}_y)

Supongamos un cilindro de radio R y longitud L imanado de esta forma. Las corrientes de magnetización son nulas en el exterior del cilindro, mientras que en el interior puede hallarse su rotacional

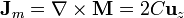
\mathbf{J}_m = \nabla\times\mathbf{M}=2C\mathbf{u}_z

Para las corrientes superficiales tenemos

  • En la base superior 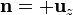\mathbf{n}=+\mathbf{u}_z y
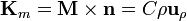
\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= C\rho\mathbf{u}_\rho\,
  • En la base inferior 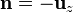\mathbf{n}=-\mathbf{u}_z y
\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= C\rho\mathbf{u}_\rho\,
Obtenido de "http://tesla.us.es/wiki/index.php/Corrientes_de_magnetizaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace