Problemas de movimiento rectilíneo (GIC)
De Laplace
(→Partícula con aceleración dependiente de x) |
|||
| Línea 10: | Línea 10: | ||
Para cada caso, haz un dibujo aproximado de la gráfica que representa el movimiento. Determina en cada caso los instantes de tiempo en los que la partícula se encuentra en el origen, en la parte positiva y en la parte negativa del eje. Si <math>x</math> se mide en metros y <math>t</math> en segundos, determina las unidades de las constantes que aparecen en las expresiones. | Para cada caso, haz un dibujo aproximado de la gráfica que representa el movimiento. Determina en cada caso los instantes de tiempo en los que la partícula se encuentra en el origen, en la parte positiva y en la parte negativa del eje. Si <math>x</math> se mide en metros y <math>t</math> en segundos, determina las unidades de las constantes que aparecen en las expresiones. | ||
| + | ==[[Coche impactando contra una pared]]== | ||
| + | Un coche impacta contra una pared a una velocidad de 100 km/h. Estima el tiempo máximo que debe tardar el airbag en desplegarse para proteger al conductor. | ||
==[[Partícula con velocidad dependiente de x]]== | ==[[Partícula con velocidad dependiente de x]]== | ||
| Línea 17: | Línea 19: | ||
==[[Partícula con aceleración dependiente de x]]== | ==[[Partícula con aceleración dependiente de x]]== | ||
Una partícula se desplaza sobre el eje <math>OX</math> de modo que su aceleración cumple en cada instante <math>a(x) = -Ax</math>, siendo <math>A</math> una constante. En la posición inicial la velocidad de la partícula es <math>v_0</math>. Determina la función <math>v(x)</math>. | Una partícula se desplaza sobre el eje <math>OX</math> de modo que su aceleración cumple en cada instante <math>a(x) = -Ax</math>, siendo <math>A</math> una constante. En la posición inicial la velocidad de la partícula es <math>v_0</math>. Determina la función <math>v(x)</math>. | ||
| - | |||
| - | |||
| - | |||
Revisión de 11:04 18 sep 2018
Contenido |
1 Problemas del boletín
1.1 Ejemplos de movimiento rectílineo
Una partícula se mueve sobre el eje OX según el movimiento dado por la siguientes expresiones. En todos los casos asumimos que el movimiento comienza en t = 0.
 .
.
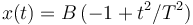 .
.
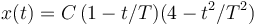 .
.
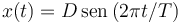 .
.
 .
.
Para cada caso, haz un dibujo aproximado de la gráfica que representa el movimiento. Determina en cada caso los instantes de tiempo en los que la partícula se encuentra en el origen, en la parte positiva y en la parte negativa del eje. Si x se mide en metros y t en segundos, determina las unidades de las constantes que aparecen en las expresiones.
1.2 Coche impactando contra una pared
Un coche impacta contra una pared a una velocidad de 100 km/h. Estima el tiempo máximo que debe tardar el airbag en desplegarse para proteger al conductor.
1.3 Partícula con velocidad dependiente de x
Una partícula se desplaza sobre el eje OX de modo que su velocidad cumple en cada instante v(x) = Ax, siendo A una constante. En el instante inicial la coordenada de la partícula es x0. Determina la función x(t).
1.4 Partícula con aceleración dependiente de x
Una partícula se desplaza sobre el eje OX de modo que su aceleración cumple en cada instante a(x) = − Ax, siendo A una constante. En la posición inicial la velocidad de la partícula es v0. Determina la función v(x).





