Entrar Página Discusión Historial Go to the site toolbox

Problemas de dinámica vectorial (CMR2)

De Laplace

(Diferencias entre revisiones)
(→Movimiento a partir de una fuerza conocida)
(→Doble máquina de Atwood)
Línea 34: Línea 34:
<center>[[Archivo:doble-maquina-atwood.png]]</center>
<center>[[Archivo:doble-maquina-atwood.png]]</center>
 +
 +
==[[Péndulo en caja deslizante]]==
 +
Una caja cúbica de gran masa desciende sin rozamiento por un plano inclinado un ángulo β. En el interior de la caja se encuentra un péndulo (de masa mucho menor que la de la caja) que cuelga de su techo.
 +
# Si el péndulo no oscila, determine el ángulo θ que forma el péndulo con la vertical.
 +
# Suponga ahora que entre la caja y el plano hay una fricción dinámica de coeficiente μ. Determine el ángulo de inclinación en ese caso.
 +
# Para los dos casos anteriores, supóngase que el péndulo se separa ligeramente de su posición de equilibrio, ¿cuál será la frecuencia de las oscilaciones que experimenta?
 +
 +
==[[Anilla ensartada en un aro (CMR)|Anilla ensartada en un aro]]==
 +
Se tiene un aro circular de radio <math>R</math> situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa <math>m</math> situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:
 +
 +
*Una anilla ensartada en el aro
 +
*Una bolita que desliza por el interior del aro, sin estar unida a él.
 +
 +
# Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
 +
# Para el caso (b), suponga que a la partícula se le comunica la velocidad inicial calculada en (a), ¿en qué punto se desprende del aro?

Revisión de 12:00 1 dic 2017

Contenido

1 Oscilador armónico tridimensional

Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico

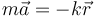
m\vec{a}=-k\vec{r}

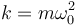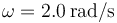con k=m\omega_0^2 y \omega = 2.0\,\mathrm{rad}/\mathrm{s}. Su posición inicial es \vec{r}_0=5\,\vec{\imath}\ (\mathrm{m}).

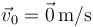  1. Para el caso \vec{v}_0=\vec{0}\,\mathrm{m}/\mathrm{s}. ¿Qué tipo de movimiento describe la partícula?
  2. Para el caso \vec{v}_0=10.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
  3. Suponga ahora que \vec{v}_0=8.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es ahora la trayectoria de la partícula?
  4. Demuestre que en todos los casos la cantidad calculada en coordenadas polares 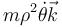m\rho^2\dot{\theta}\vec{k} es constante.

2 Dos masas unidas por un muelle

Dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 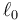\ell_0. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 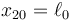x_{20}=\ell_0. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.

  1. Determine dos constantes de movimiento.
  2. Calcule la posición de cada una de las masas como función del tiempo. Sugerencia: realice el cambio de variables xG = (m1x1 + m2x2) / (m1 + m2), x=x_2-x_1-\ell_0.

3 Dos masas unidas por un oscilador armónico

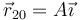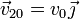Suponga que en el problema “Oscilador armónico tridimensional” en lugar de una sola partícula tenemos dos, de masas m1 y m2, unidas por un resorte de constante k y longitud natural nula. Inicialmente la masa 1 se halla en reposo en el origen de coordenadas y la masa 2 se encuentra en \vec{r}_{20}=A\vec{\imath} moviéndose con velocidad \vec{v}_{20}=v_0\vec{\jmath}.

  1. Demuestre que el centro de masas de las dos partículas describe un movimiento rectilíneo y uniforme.
  2. Considerando la posición de cada partícula respecto al CM, determine la posición de cada una de ellas como función del tiempo.

4 Movimiento a partir de una fuerza conocida

Una partícula material de masa m parte del origen de coordenadas con velocidad 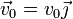\vec{v}_0=v_0\vec{\jmath}, encontrándose sometida en todo momento a la fuerza dependiente de la posición

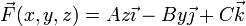
\vec{F}(x,y,z)=Az\vec{\imath}-By\vec{\jmath}+C\vec{k}

siendo 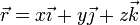\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k} la posición instantánea de la partícula, y A, B y C constantes positivas conocidas.

Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, t.

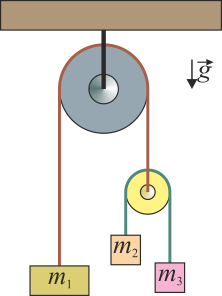
5 Doble máquina de Atwood

La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales (inextensibles y sin masa) y dos poleas también ideales (de masa despreciable y sin rozamiento). Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.

Archivo:doble-maquina-atwood.png

6 Péndulo en caja deslizante

Una caja cúbica de gran masa desciende sin rozamiento por un plano inclinado un ángulo β. En el interior de la caja se encuentra un péndulo (de masa mucho menor que la de la caja) que cuelga de su techo.

  1. Si el péndulo no oscila, determine el ángulo θ que forma el péndulo con la vertical.
  2. Suponga ahora que entre la caja y el plano hay una fricción dinámica de coeficiente μ. Determine el ángulo de inclinación en ese caso.
  3. Para los dos casos anteriores, supóngase que el péndulo se separa ligeramente de su posición de equilibrio, ¿cuál será la frecuencia de las oscilaciones que experimenta?

7 Anilla ensartada en un aro

Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa m situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:

  • Una anilla ensartada en el aro
  • Una bolita que desliza por el interior del aro, sin estar unida a él.
  1. Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
  2. Para el caso (b), suponga que a la partícula se le comunica la velocidad inicial calculada en (a), ¿en qué punto se desprende del aro?
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_din%C3%A1mica_vectorial_(CMR2)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace