Primera Convocatoria Ordinaria 2014/15 (G.I.A.)
De Laplace
(Página creada con '== Partícula moviéndose sobre una hélice== [[Imagen:G1_GIA_PPC_2015_particula_sobre_helice_enunciado.png|rig…') |
(→Partícula moviéndose sobre una hélice) |
||
| Línea 1: | Línea 1: | ||
| + | ==[[Vector rotación de un punto recorriendo una circunferencia, Enero 2015 (F1 GIA)| Vector rotación de un punto recorriendo una circunferencia]]== | ||
| + | [[Imagen:F1_GIA_PCO_2014_vector_rotacion_plano.png|right]] | ||
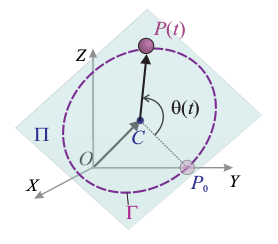
| + | Un punto material <math>P </math> se mueve recorriendo la circunferencia <math>\Gamma </math>, contenida en un plano <math>\Pi </math>, cuya ecuación paramétrica es | ||
| + | <center> | ||
| + | <math> | ||
| + | \Pi : \overrightarrow{OX} = \overrightarrow{OC} + \lambda\,\vec{a} + \mu\,\vec{b}, \quad \lambda, \mu \in \mathbb{R} | ||
| + | </math> | ||
| + | </center> | ||
| + | donde <math>C </math> es el centro de la circunferencia. Para describir analíticamente las magnitudes vectoriales se adopta un sistema de referencia cartesiano <math>OXYZ </math>, en el cual <math>\vec{a} = 2\,\vec{\imath} - \vec{\jmath} </math> y <math>\vec{b} = \vec{\jmath} - \vec{k} </math>, y la posición de <math>C </math> está determinada por el segmento orientado <math>\overrightarrow{OC}=\vec{\jmath} + \vec{k} </math> (con las componentes medidas en metros). En el instante inicial <math>(t=0) </math>, el punto móvil <math>P </math> ocupa la posición determinada por el segmento orientado <math>\overrightarrow{OP}_0 = 2\,\vec{\jmath} </math>. A partir de ésta, la partícula realiza un movimiento circular uniforme, con velocidad de <math>2\,\mathrm{m/s} </math>. Determine el vector rotación instantánea <math>\vec{\omega}_0 </math> que caracteriza este movimiento circular. | ||
| + | |||
==[[Partícula moviéndose sobre una hélice, Enero 2015 (F1 GIA)| Partícula moviéndose sobre una hélice]]== | ==[[Partícula moviéndose sobre una hélice, Enero 2015 (F1 GIA)| Partícula moviéndose sobre una hélice]]== | ||
[[Imagen:G1_GIA_PPC_2015_particula_sobre_helice_enunciado.png|right]] | [[Imagen:G1_GIA_PPC_2015_particula_sobre_helice_enunciado.png|right]] | ||
Revisión de 14:27 30 ene 2015
1 Vector rotación de un punto recorriendo una circunferencia
Un punto material P se mueve recorriendo la circunferencia Γ, contenida en un plano Π, cuya ecuación paramétrica es
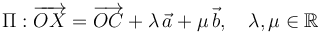
donde C es el centro de la circunferencia. Para describir analíticamente las magnitudes vectoriales se adopta un sistema de referencia cartesiano OXYZ, en el cual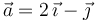 
y 
, y 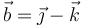la posición de C está determinada por el segmento orientado 
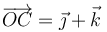(con las componentes medidas en metros). En el instante inicial (t = 0), el punto móvil P ocupa la posición determinada por el segmento orientado 
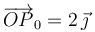. A partir de ésta, la partícula realiza un movimiento circular uniforme, con velocidad de 
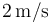. Determine el vector rotación instantánea 
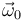que caracteriza este movimiento circular.
2 Partícula moviéndose sobre una hélice
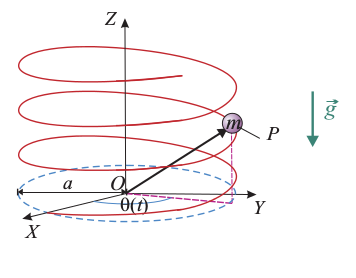
Una partícula P de masa m está insertada en la hélice fija y uniforme Γ. Utilizando un sistema de referencia cartesiano OXYZ, en el cuál la gravedad está descrita analíticamente por el vector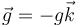 
, la ecuación parámetrica de dicha hélice es:
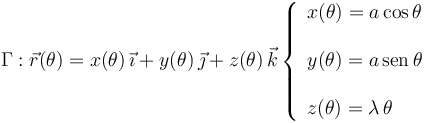
donde a y λ son constantes. EL parámetro geométrico θ es el ángulo que forma con el eje OX la proyección del radio-vector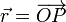 
sobre el plano horizontal OXY. Cuando la partícula recorre la hélice Γ, sin rozamiento apreciable, su movimiento queda descrito por la ley horaria θ(t).
- Determine cuál debe ser el valor de la constante λ para que el radio de curvatura de la hélice sea Rκ = 3a / 2. ¿Qué distancia h asciende la partícula en la dirección vertical cada vez que da una vuelta completa alrededor del eje OZ.
- Obtenga la expresiones de las componentes intrínsecas de la velocidad y la aceleración en términos de la ley horaria θ(t) y/o sus derivadas.
- Discuta razonadamente si se verificará la conservación (total o parcial) del momento cinético
de la partícula, calculado respecto del punto fijo O.
