Vector rotación de un punto recorriendo una circunferencia, Enero 2015 (F1 GIA)
De Laplace
1 Enunciado
2 Vector rotación de un punto recorriendo una circunferencia
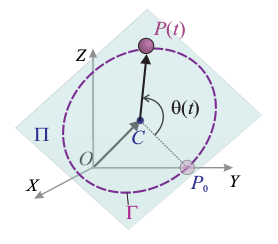
Un punto material P se mueve recorriendo la circunferencia Γ, contenida en un plano Π, cuya ecuación paramétrica es
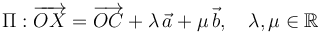
donde C es el centro de la circunferencia. Para describir analíticamente las magnitudes vectoriales se adopta un sistema de referencia cartesiano OXYZ, en el cual 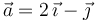 y
y 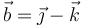 , y la posición de C está determinada por el segmento orientado
, y la posición de C está determinada por el segmento orientado 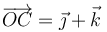 (con las componentes medidas en metros). En el instante inicial (t = 0), el punto móvil P ocupa la posición determinada por el segmento orientado
(con las componentes medidas en metros). En el instante inicial (t = 0), el punto móvil P ocupa la posición determinada por el segmento orientado 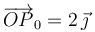 . A partir de ésta, la partícula realiza un movimiento circular uniforme, con velocidad de
. A partir de ésta, la partícula realiza un movimiento circular uniforme, con velocidad de 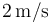 . Determine el vector rotación instantánea
. Determine el vector rotación instantánea 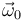 que caracteriza este movimiento circular.
que caracteriza este movimiento circular.
3 Solución
El vector rotación es perpendicular al plano. El plano es paralelo a los vectores  y
y  , por lo que podemos encontrar un vector perpendicular al plano de módulo unidad usando el producto vectorial
, por lo que podemos encontrar un vector perpendicular al plano de módulo unidad usando el producto vectorial
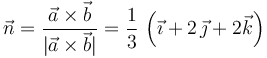
El vector rotación es
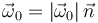
Obtenemos el módulo de 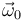 a partir de la rapidez de la partícula. Si C es el centro de la circunferencia y P es un punto cualquiera de ella, la velocidad de la partícula puede calcularse como
a partir de la rapidez de la partícula. Si C es el centro de la circunferencia y P es un punto cualquiera de ella, la velocidad de la partícula puede calcularse como
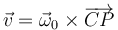
Pero estos vectores son perpendiculares, por lo que el módulo de la velocidad es
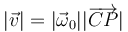
El radio de la circunferencia es 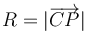 . Esto es cierto para cualquier punto de la circunferencia, en concreto para P0. Tenemos entonces
. Esto es cierto para cualquier punto de la circunferencia, en concreto para P0. Tenemos entonces
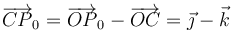
y entonces
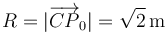
El módulo del vector rotación es
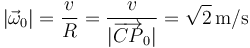
Y el vector rotación es
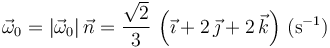
Hay una ambigüedad en el sentido de 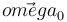 . En el examen se aceptaban como válidos los dos posibles.
. En el examen se aceptaban como válidos los dos posibles.