Problemas de electrostática en medios materiales (GIE)
De Laplace
(→Carga en el interior de una corona esférica) |
(→Esfera conductora en equilibrio electrostático) |
||
| Línea 10: | Línea 10: | ||
Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 12\,\mathrm{V}</math>. | Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 12\,\mathrm{V}</math>. | ||
| + | |||
| + | ==[[Esfera que se conecta a una fuente de tensión]]== | ||
| + | Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga <math>Q_1=10\,\mathrm{nC}</math>. Alrededor de la esfera no hay más conductores ni cargas. | ||
| + | |||
| + | |||
| + | <center><math>esfera-fuente.png</math></center> | ||
| + | |||
| + | # Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema. | ||
| + | # Suponga que ahora se conecta a la esfera una fuente de tensión de 3.0 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera? | ||
| + | # Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema? | ||
| + | # ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia? | ||
| + | # Determine la ecuación diferencial que gobierna el potencial <math>V(t)</math> de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de <math>V(t)</math> frente al tiempo. | ||
| + | |||
| + | \textbf{Dato:} $1/(4\pi\varepsilon_0) = 9\times 10^9\,\mathrm{m}/\mathrm{F}$ | ||
==[[Carga en el interior de una corona esférica]]== | ==[[Carga en el interior de una corona esférica]]== | ||
Revisión de 09:55 21 jun 2013
1 Esfera conductora en equilibrio electrostático
Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:
- el potencial y el campo eléctrico en todos los puntos del espacio.
- el voltaje al que se encuentra
- la densidad superficial de carga.
- la energía electrostática que almacena.
Particularice los resultados anteriores para un radio  y una carga
y una carga 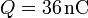 .
.
Suponga ahora que lo que se conoce inicialmente su voltaje V0, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje 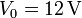 .
.
2 Esfera que se conecta a una fuente de tensión
Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga 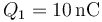 . Alrededor de la esfera no hay más conductores ni cargas.
. Alrededor de la esfera no hay más conductores ni cargas.
- Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
- Suponga que ahora se conecta a la esfera una fuente de tensión de 3.0 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
- Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
- ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
- Determine la ecuación diferencial que gobierna el potencial V(t) de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de V(t) frente al tiempo.
\textbf{Dato:} $1/(4\pi\varepsilon_0) = 9\times 10^9\,\mathrm{m}/\mathrm{F}$
3 Carga en el interior de una corona esférica
Se tiene un conductor metálico en forma de corona esférica de radio interior 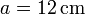 y exterior
y exterior 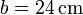 . En el centro de la
cavidad esférica se encuentra una carga puntual
. En el centro de la
cavidad esférica se encuentra una carga puntual 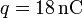 . Calcule:
. Calcule:
- La carga en cada uno de las superficies del conductor.
- El potencial al que se encuentra la carga y el conductor
- El campo eléctrico en el exterior de la esfera y en la cavidad.
- La energía electrostática almacenada.
para los siguientes cuatro casos:
- La corona esférica está conectada a tierra.
- La corona está aislada y descargada.
- La corona está conecta a una fuente de tensión que fija un voltaje
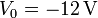 .
.
- La corona está aislada y almacena una carga
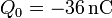 .
.
4 Esfera rodeada de corona esférica
Se tiene una esfera conductora de radio a que almacena una carga Q0. Rodeándola se halla una corona esférica también conductora de radio interior 2a y exterior 4a. Esta corona se halla inicialmente aislada y descargada.
- Calcule el campo eléctrico en todos los puntos del espacio. Puede suponerse que las distribuciones de carga son todas uniformes.
- Determine el potencial al que se encuentra la esfera interior.
- Calcule la energía electrostática almacenada en el sistema.
- Suponga que se conecta la corteza exterior a tierra. Una vez que se vuelve al equilibrio electrostático, ¿cómo cambia el potencial de la esfera interior y la energía almacenada? ¿A qué se debe la diferencia de energía?
5 Conexión de dos esferas alejadas
Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q0.
- ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
- ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?

6 Condensador plano de placas circulares
Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V.
Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa 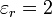 . ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
. ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
7 Tres placas conductoras paralelas
Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm y ésta de la tercera 0.8 mm. Halle:
- La carga almacenada en cada placa.
- El potencial al que se encuentra cada una.
- El campo eléctrico entre las placas.
- La energía almacenada en el sistema.
para los siguientes casos:
- La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra.
- La placa central está a 24 V y las otras dos a tierra.
- La primera está a −24 V, la central a +24 V y la tercera a tierra.
8 Cuatro placas conductoras paralelas
Se colocan paralelamente cuatro placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm, ésta de la tercera 0.4 mm, y esta de la cuarta 0.6 mm. Las dos placas centrales están aisladas y descargadas. Se coloca la primera placa a 100 V y la última a tierra. Halle el voltaje y la carga de cada placa, así como la energía almacenada.
Sin descargar las placas se desconecta la fuente de tensión. A continuación se conecta por un hilo metálico la segunda con la tercera placa. Halle las nuevas cargas, voltajes y energía almacenada.
¿Cómo cambian los resultados se conectan las placas centrales sin desconectar previamente la fuente de tensión? ¿Qué trabajo realiza la fuente en este caso?
9 Sistema de cuatro condensadores
El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: 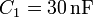 ,
, 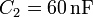 ,
, 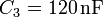 y
y 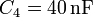 . La diferencia de potencial entre A y B es de
. La diferencia de potencial entre A y B es de 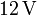 . ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
. ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?
10 Condensador que se rellena parcialmente de dieléctrico
El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.
Entre las placas se establece una diferencia de potencial de 20 V
- ¿Cuánto vale la energía almacenada en el sistema?
- Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (
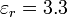 ) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
- Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?
11 Capacidad de la tierra y la ionosfera
La tierra y la ionosfera pueden considerarse que forman un condensador esférico. Si el radio de la tierra es de aproximadamente 6400 km y la ionosfera está a 100 km de altura, ¿cuánto vale la capacidad de este condensador?
12 Condensador que se gira 90°
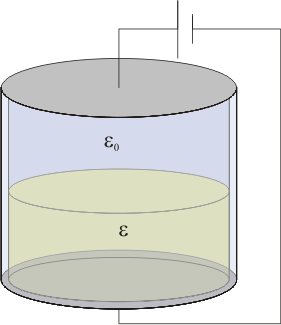
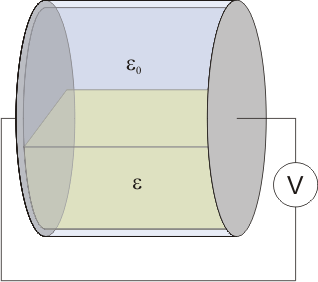
Se construye un recipiente cilíndrico, con bases perfectamente conductoras de sección S, separadas una distancia a, y paredes perfectamente dieléctricas, de espesor despreciable. El interior se llena hasta la mitad con un líquido dieléctrico y permitividad  . El resto se deja vacío.
. El resto se deja vacío.
El recipiente se coloca en un principio con las bases dispuestas horizontalmente. En esta posición, se carga hasta que la diferencia de potencial entre las placas es V0. Acto seguido se abre el circuito y, sin descargar las placas, el recipiente es girado 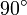 alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
Desprecie los efectos de borde y la influencia de las paredes.