Condensador que se gira 90°

De Laplace

1 Enunciado

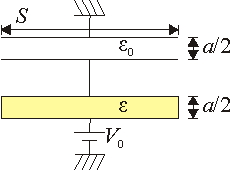
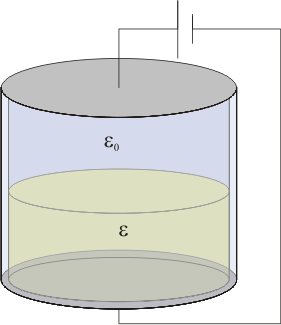
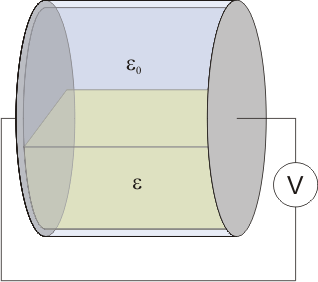
Se construye un recipiente cilíndrico, con bases perfectamente conductoras de sección $S$ , separadas una distancia $a$ , y paredes perfectamente dieléctricas, de espesor despreciable. El interior se llena hasta la mitad con un líquido dieléctrico y permitividad $\varepsilon$ . El resto se deja vacío.

El recipiente se coloca en un principio con las bases dispuestas horizontalmente. En esta posición, se carga hasta que la diferencia de potencial entre las placas es $V 0$ . Acto seguido se abre el circuito y, sin descargar las placas, el recipiente es girado $90^\circ$ alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?

Desprecie los efectos de borde y la influencia de las paredes.

2 Antes de la rotación

En el primer estado, al ser las bases horizontales, el líquido se coloca formando una capa que llena hasta la mitad el recipiente. El problema es entonces análogo al de un condensador de placas planas y paralelas formado por dos capas de dieléctrico. En este caso, la permitividad de una es $\varepsilon$ , mientras que la otra es $\varepsilon_0$ (por estar vacía).

La capacidad en esta configuración es equivalente a la de una asociación en serie de dos condensadores de capacidades

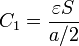
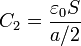
$C_1=\frac{\varepsilon{}S}{a/2}$ $C_2=\frac{\varepsilon_0 S}{a/2}$

por ser $a / 2$ el espesor de cada capa. La capacidad equivalente se obtiene de

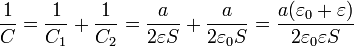
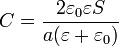
$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}=\frac{a}{2\varepsilon{}S}+ \frac{a}{2\varepsilon_0 S}=\frac{a(\varepsilon_0+\varepsilon{})}{2\varepsilon_0\varepsilon{}S}$ $\Rightarrow$ $C=\frac{2\varepsilon_0\varepsilon{}S}{a(\varepsilon{}+\varepsilon_0)}$

Al establecer una diferencia de potencial $V 0$ entre las placas se almacena una carga en el condensador

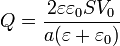
$Q=\frac{2\varepsilon{}\varepsilon_0 SV_0}{a(\varepsilon{}+\varepsilon_0)}$

3 Después de la rotación

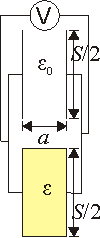
Cuando se gira el recipiente, el líquido sigue llenado hasta la mitad su interior, pero ahora su superficie es ortogonal a las bases. Tenemos entonces

un condensador formado por una asociación en paralelo de otros dos, siendo la capacidad de cada uno

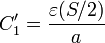
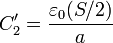
$C'_1=\frac{\varepsilon{} (S/2)}{a}$ $C'_2=\frac{\varepsilon_0 (S/2)}{a}$

siendo ahora $S / 2$ la sección de cada condensador y $a$ su espesor. La capacidad total es

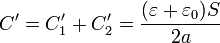
$C'=C'_1+C'_2=\frac{(\varepsilon{}+\varepsilon_0)S}{2a}$

Al efectuar la rotación, esta se hace con las placas cargadas, siendo el valor de la carga acumulada el obtenido en la configuración anterior.

Esta nueva capacidad es mayor que la anterior, ya que

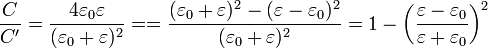
$\frac{C}{C'}= \frac{4\varepsilon_0\varepsilon{}}{(\varepsilon_0+\varepsilon{})^2} = =\frac{(\varepsilon_0+\varepsilon{})^2-(\varepsilon{}-\varepsilon_0)^2}{(\varepsilon_0+\varepsilon{})^2}= 1-\left(\frac{\varepsilon{}-\varepsilon_0}{\varepsilon{}+\varepsilon_0}\right)^2$

y el segundo término es siempre positivo, por lo que $C / C' < 1$ .

En este caso, la nueva diferencia de potencial entre las placas es

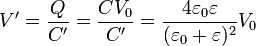
$V'=\frac{Q}{C'}=\frac{CV_0}{C'}=\frac{4\varepsilon_0\varepsilon{}}{(\varepsilon_0+\varepsilon{})^2}V_0$

Esta nueva diferencia de potencial es siempre inferior a la original.

Este resultado implica que al rotar el recipiente se pierde energía. La energía inicial vale

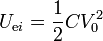
$U_{\mathrm{e}i} = \frac{1}{2}C V_0^2$

y la final

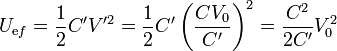
$U_{\mathrm{e}f} = \frac{1}{2}C' V'^2 = \frac{1}{2}C'\left(\frac{CV_0}{C'}\right)^2 = \frac{C^2}{2C'}V_0^2$

La variación de la energía en el proceso es

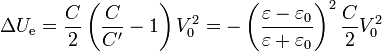
$\Delta U_\mathrm{e} = \frac{C}{2}\left(\frac{C}{C'}-1\right)V_0^2 = -\left(\frac{\varepsilon{}-\varepsilon_0}{\varepsilon{}+\varepsilon_0}\right)^2\frac{C}{2}V_0^2$

La energía perdida puede haberse disipado en forma de calor y haberse absorbido por el agente mecánico que efectúa la rotación del sistema.

Condensador que se gira 90°

De Laplace

1 Enunciado

2 Antes de la rotación

3 Después de la rotación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES