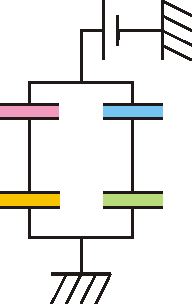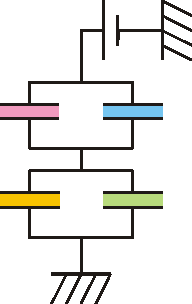Sistema de cuatro condensadores

De Laplace

Contenido

1 Enunciado
2 Antes de la conexión
3 Después de la conexión
4 Solución general

1 Enunciado

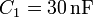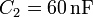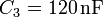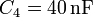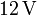El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: $C_1=30\,\mathrm{nF}$ , $C_2=60\,\mathrm{nF}$ , $C_3=120\,\mathrm{nF}$ y $C_4=40\,\mathrm{nF}$ . La diferencia de potencial entre A y B es de $12\,\mathrm{V}$ .

¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E?
Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?

2 Antes de la conexión

Tenemos que, para cada uno de los condensadores de la rama superior se cumple

$\Delta V_1= V_A-V_D = \frac{Q_1}{C_1}\qquad\qquad \Delta V_2=V_D-V_B = \frac{Q_2}{C_2}$

pero, por estar el punto D desconectado de cualquier otra fuente o elemento, los dos condensadores $C 1$ y $C 2$ están en serie y la carga en ambos es la misma

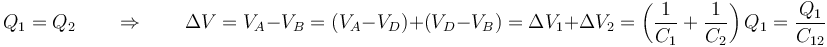
$Q_1 = Q_2\qquad\Rightarrow\qquad \Delta V = V_A-V_B = (V_A-V_D)+(V_D-V_B)=\Delta V_1+\Delta V_2 = \left(\frac{1}{C_1}+\frac{1}{C_2}\right)Q_1 = \frac{Q_1}{C_{12}}$

siendo $C 12$ la capacidad del condensador equivalente a esta rama. Puesto que conocemos la diferencia de potencial total y la capacidad de cada condensador, podemos hallar la carga en cada uno

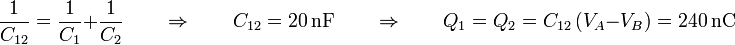
$\frac{1}{C_{12}}=\frac{1}{C_1}+\frac{1}{C_2}\qquad\Rightarrow\qquad C_{12}=20\,\mathrm{nF}\qquad\Rightarrow\qquad Q_1 = Q_2 = C_{12}\,(V_A-V_B) = 240\,\mathrm{nC}$

Una vez que tenemos la carga en cada uno, podemos hallar las respectivas diferencias de potencial

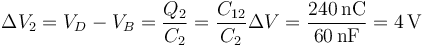
$\Delta V_2 = V_D -V_B = \frac{Q_2}{C_2}=\frac{C_{12}}{C_2}\Delta V = \frac{240\,\mathrm{nC}}{60\,\mathrm{nF}}=4\,\mathrm{V}$

y

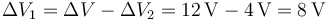
$\Delta V_1 = \Delta V-\Delta V_2 = 12\,\mathrm{V}-4\,\mathrm{V}=8\,\mathrm{V}$

Operando del mismo modo hallamos la carga de los condensadores de la rama inferior

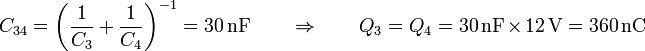
$C_{34}=\left(\frac{1}{C_3}+\frac{1}{C_4}\right)^{-1}= 30\,\mathrm{nF}\qquad\Rightarrow\qquad Q_3 = Q_4 = 30\,\mathrm{nF}\times 12\,\mathrm{V} =360\,\mathrm{nC}$

y el voltaje del punto E respecto al B

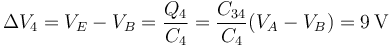
$\Delta V_4 = V_E -V_B= \frac{Q_4}{C_4}=\frac{C_{34}}{C_4}(V_A-V_B) = 9\,\mathrm{V}$

Por tanto la diferencia de potencial entre ambos puntos es

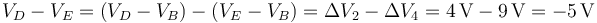
$V_D - V_E = (V_D-V_B)-(V_E-V_B) = \Delta V_2-\Delta V_4= 4\,\mathrm{V}-9\,\mathrm{V}=-5\,\mathrm{V}$

Las cargas de cada uno de los condensadores son, según se ha dicho

$Q_1 = Q_2 = 240\,\mathrm{nC}\qquad\qquad Q_3 = Q_4 = 360\,\mathrm{nC}$

La carga del condensador equivalente a toda la asociación es la suma de las de las dos ramas

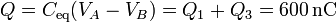
$Q=C_\mathrm{eq}(V_A-V_B) = Q_1+Q_3=600\,\mathrm{nC}$

siendo la capacidad del condensador equivalente la correspondiente a una asociación en paralelo de dos condensadores

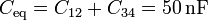
$C_\mathrm{eq}=C_{12}+C_{34}= 50\,\mathrm{nF}$

Las diferencias de potencial respectivas valen

$\Delta V_1 = V_A-V_D = 8\,\mathrm{V}\qquad\qquad \Delta V_2 = V_D-V_B = 4\,\mathrm{V}$ $\Delta V_3 = V_A-V_E = 3\,\mathrm{V}\qquad\qquad\Delta V_4 = V_E-V_B = 9\,\mathrm{V}$

La energía almacenada en el condensador la podemos hallar sumando la almacenada en cada uno de ellos

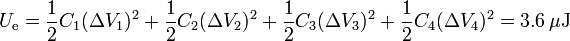
$U_\mathrm{e}=\frac{1}{2}C_1(\Delta V_1)^2+\frac{1}{2}C_2(\Delta V_2)^2+\frac{1}{2}C_3(\Delta V_3)^2+\frac{1}{2}C_4(\Delta V_4)^2=3.6\,\mu\mathrm{J}$

También podemos hallarla considerando que todo el sistema es equivalente un solo condensador

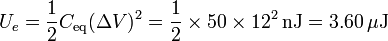
$U_e = \frac{1}{2}C_\mathrm{eq}(\Delta V)^2= \frac{1}{2}\times 50\times 12^2\,\mathrm{nJ}=3.60\,\mu\mathrm{J}$

3 Después de la conexión

Una vez que se cierra el interruptor, la topología del circuito cambia. Al conectarse los dos puntos D y E, se produce un flujo de carga desde el punto a mayor voltaje, el E, al de menor potencial, el E. Como resultado, se alteran las cargas en los cuatro condensadores.

Ahora, en lugar de tener una asociación en paralelo de dos asociaciones en serie, tenemos una asociación en serie de dos asociaciones en paralelo (la del 1 con el 3 y la del 2 con el 4).

Las capacidades de las dos asociaciones en paralelo valen

$C_{13}=C_1+C_3 = 150\,\mathrm{nF}\qquad\qquad C_{24}=C_2+C_4=100\,\mathrm{nF}$

siendo la total de la asociación de cuatro condensadores

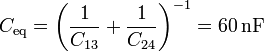
$C_\mathrm{eq}=\left(\frac{1}{C_{13}}+\frac{1}{C_{24}}\right)^{-1}=60\,\mathrm{nF}$

Nótese que no coincide con la capacidad equivalente total del apartado anterior, que era de 50 nF. El cerrar el interruptor cambia la capacidad del sistema, aunque cada condensador mantenga su capacidad.

La carga del condensador equivalente es

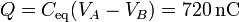
$Q=C_\mathrm{eq}(V_A-V_B) = 720\,\mathrm{nC}$

Vemos que tampoco coincide con la total del apartado anterior, que era de 600 nC, es decir, que para mantener la diferencia de potencial, la fuente de tensión debe introducir una carga adicional en el sistema.

El voltaje del punto D (y el punto E) lo hallamos como en el apartado anterior

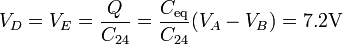
$V_D = V_E = \frac{Q}{C_{24}}=\frac{C_\mathrm{eq}}{C_{24}}(V_A-V_B) = 7.2\mathrm{V}$

Una vez que conocemos el voltaje del punto central podemos hallar la carga de cada condensador

$Q_1 = C_1(V_A-V_D) = 144\,\mathrm{nC}\qquad\qquad Q_2 = C_2(V_D-V_B) = 432\,\mathrm{nC}\qquad\qquad Q_3 = C_3(V_A-V_D) = 576\,\mathrm{nC}\qquad\qquad Q_4 = C_4(V_D-V_B) = 288\,\mathrm{nC}$

La nueva energía almacenada la hallamos a partir de la capacidad del circuito equivalente

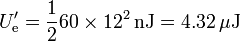
$U'_\mathrm{e}=\frac{1}{2}60\times 12^2\,\mathrm{nJ}=4.32\,\mu\mathrm{J}$

La variación en la energía como consecuencia de la conexión es

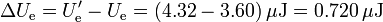
$\Delta U_\mathrm{e}=U'_\mathrm{e}-U_\mathrm{e}=(4.32-3.60)\,\mu\mathrm{J}=0.720\,\mu\mathrm{J}$

En este proceso, el generador ha metido un trabajo en el sistema igual a la cantidad de carga introducida multiplicada por el potencial al que lo pone

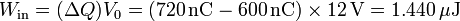
$W_\mathrm{in}=(\Delta Q)V_0 = (720\,\mathrm{nC}-600\,\mathrm{nC})\times 12\,\mathrm{V}=1.440\,\mu\mathrm{J}$

Puesto que este trabajo supera al aumento de la energía interna concluimos, por el primer principio de la termodinámica, que también ha habido un intercambio de calor

$Q_\mathrm{out}=W_\mathrm{in}-\Delta U = 0.720\,\mu\mathrm{J}$

4 Solución general

Los dos apartados pueden resolverse de forma general plantenado un sistema de ecuaciones común.

Para los cuatro condensadores, definiendo la carga de cada uno como la que está en la placa de la izquierda tenemos

$\begin{array}{rclcrcl} Q_1 & = & C_1(V_A-V_D) & \qquad\qquad & Q_2 & = & C_2(V_D-V_B) \\ Q_3 & = & C_3(V_A-V_E) & \qquad\qquad & Q_4 & = & C_4(V_D-V_B) \end{array}$

Numéricamente, si medimos el potencial en voltios, la carga en nanoculombios y la capacidad en nanofaradios

$\begin{array}{rclcrcl} Q_1 & = & 30(V_A-V_D) & \qquad\qquad & Q_2 & = & 60(V_D-V_B) \\ Q_3 & = & 120(V_A-V_E) & \qquad\qquad & Q_4 & = & 40(V_D-V_B) \end{array}$

Además conocemos la diferencia de potencial entre los extremos

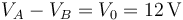
$V_A - V_B = V_0=12\,\mathrm{V}$

Para completar el sistema nos bastan dos ecuaciones más:

En el primer caso, el nodo D y el nodo E, por separado representan conductores descargados y por tanto

$-Q_1+Q_2=0\qquad\qquad -Q_3 + Q_4 = 0$

En el segundo caso, el nodo D y el nodo E forman parte del mismo conductor descargado

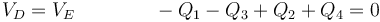
$V_D = V_E \qquad\qquad -Q_1-Q_3+Q_2+Q_4 = 0$

A partir de aquí la solución es pura manipulación algebraica, equivalente a las soluciones ya indicadas.

Sistema de cuatro condensadores

De Laplace

Contenido

1 Enunciado

2 Antes de la conexión

3 Después de la conexión

4 Solución general

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES