Cilindro imanado en dirección acimutal
De Laplace
(→Campos magnéticos) |
|||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 44: | Línea 44: | ||
* En la cara lateral <math>\mathbf{n}=\mathbf{u}_\rho</math> | * En la cara lateral <math>\mathbf{n}=\mathbf{u}_\rho</math> | ||
| - | <center><math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= - | + | <center><math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= -CR\mathbf{u}_z\,</math></center> |
| + | |||
| + | Nótese que deben sustituirse las coordenadas por su valor en la superficie. En los dos primeros casos, <math>\rho</math> varía desde 0 a <math>R</math>, por lo que se deja como variable, pero para la cara lateral posee un valor constante <math>\rho = R</math>, que debe sustituirse. | ||
Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación. | Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación. | ||
==Cargas magnéticas== | ==Cargas magnéticas== | ||
| + | Las densidades de carga magnética equivalentes a esta magnetización pueden también ser de volumen o superficiales. | ||
| + | |||
| + | ===De volumen=== | ||
| + | En el exterior del cilindro la densidad es nula, por serlo la imanación. | ||
| + | |||
| + | <center><math>\rho_m = -\nabla\cdot\mathbf{M} = 0</math></center> | ||
| + | |||
| + | En el interior la densidad de carga también es nula, por ser este [[Cálculo_de_divergencias_y_rotacionales#Campo_B|campo solenoidal]] | ||
| + | |||
| + | <center><math>\rho_m = -\nabla\cdot\mathbf{M} = -C\left(-\frac{\partial y}{\partial x}+\frac{\partial x}{\partial y}\right)=0</math></center> | ||
| + | |||
| + | ===De superficie=== | ||
| + | Como en el caso de las corrientes de imanación, tenemos posibles densidades de carga magnética en las bases y en la cara lateral. La expresión general de las cargas magnéticas en una interfaz es | ||
| + | |||
| + | <center><math>\sigma_m = -\mathbf{n}\cdot[\mathbf{M}]\,</math></center> | ||
| + | |||
| + | que, para el caso de que una de las dos regiones sea el vacío, se reduce a | ||
| + | |||
| + | <center><math>\sigma_m = \mathbf{M}\cdot\mathbf{n}\,</math></center> | ||
| + | |||
| + | En nuestro caso, tenemos | ||
| + | |||
| + | * En la base superior <math>\mathbf{n}=+\mathbf{u}_z</math> y | ||
| + | |||
| + | <center><math>\sigma_m = \mathbf{M}\cdot\mathbf{n}= 0\,</math></center> | ||
| + | |||
| + | * En la base inferior <math>\mathbf{n}=-\mathbf{u}_z</math> y | ||
| + | |||
| + | <center><math>\sigma_m = \mathbf{M}\cdot\mathbf{n}=0</math></center> | ||
| + | |||
| + | * En la cara lateral <math>\mathbf{n}=\mathbf{u}_\rho</math> | ||
| + | |||
| + | <center><math>\sigma_m = \mathbf{M}\cdot\mathbf{n}= 0</math></center> | ||
| + | |||
| + | En las tres superficies la imanación es perpendicular al vector normal, por ser la imanación acimutal. | ||
| + | |||
==Campos magnéticos== | ==Campos magnéticos== | ||
| + | Podemos hallar los campos magnéticos a partir de las corrientes de imanación. Así calcularíamos <math>\mathbf{B}</math> y luego <math>\mathbf{H}</math>. | ||
| + | |||
| + | Sin embargo es mucho más sencillo hallar primero <math>\mathbf{H}</math>, cuyas fuentes son las corrientes libres y las cargas magnéticas, y a partir de ahí calcular <math>\mathbf{B}</math>. La razón es obvia: tanto las corrientes libres como las cargas magnéticas son nulas. | ||
| + | |||
| + | Las ecuaciones generales para el campo <math>\mathbf{H}</math> son | ||
| + | |||
| + | <center><math>\begin{matrix}\nabla\cdot\mathbf{H}=\rho_m & \qquad & \mathbf{n}\cdot[\mathbf{H}]=\sigma_m \\ & & \\ | ||
| + | \nabla\times\mathbf{H}=\mathbf{J}_l & \qquad & \mathbf{n}\times[\mathbf{H}]=\mathbf{K}_l \end{matrix}</math></center> | ||
| + | |||
| + | En este problema, en el que solo tenemos un material imanado y no hay aplicada ninguna corriente libre de origen externo, las corrientes libres son nulas | ||
| + | |||
| + | <center><math>\mathbf{J}_l = \mathbf{0}\,</math>{{qquad}}{{qquad}}<math>\mathbf{K}_l = \mathbf{0}\,</math></center> | ||
| + | |||
| + | Asimismo, hemos calculado en el apartado anterior que las densidades de carga magnética son nulas, tanto en el volumen, como en las interfaces | ||
| + | |||
| + | <center><math>\rho_m = 0\,</math>{{qquad}}{{qquad}}<math>\sigma_m = 0\,</math></center> | ||
| + | |||
| + | Además, por ser el sistema de tamaño finito, el campo magnético que produce tiende a cero en puntos alejados | ||
| + | |||
| + | <center><math>\mathbf{H}\to\mathbf{0}\qquad(r\to\infty)</math></center> | ||
| + | |||
| + | Según esto, el campo magnético <math>\mathbf{H}</math> carece de fuentes escalares y vectoriales y decae en el infinito. Por tanto, el campo <math>\mathbf{H}</math> es nulo en todo el espacio: | ||
| + | |||
| + | <center><math>\mathbf{H}=\mathbf{0}\,</math></center> | ||
| + | |||
| + | y, una vez que tenemos el campo <math>\mathbf{H}</math> tenemos el campo <math>\mathbf{B}</math> | ||
| + | |||
| + | <center><math>\mathbf{B}=\mu_0\left(\mathbf{H}+\mathbf{M}\right)=\mu_0\mathbf{M}=\begin{cases}\mu_0C\rho\mathbf{u}_\varphi & \mathrm{interior} \\ & \\ \mathbf{0} & \mathrm{exterior}\end{cases}</math></center> | ||
| + | |||
[[Categoría:Problemas de materiales magnéticos]] | [[Categoría:Problemas de materiales magnéticos]] | ||
última version al 11:47 16 nov 2009
Contenido |
1 Enunciado
Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, expresable en cilíndricas o cartesianas como
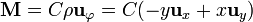
Supongamos un cilindro de radio R y longitud L imanado de esta forma.
- Calcule las corrientes de imanación equivalentes a esta magnetización.
- Halle las cargas magnéticas equivalentes a esta barra.
- Determine los campos magnético
 y
y  en este sistema.
en este sistema.
2 Corrientes de magnetización
2.1 Volumétricas
Las corrientes de magnetización en el volumen se calculan como

Estas corrientes son nulas son nulas en el exterior del cilindro, mientras que en el interior puede hallarse el rotacional de la imanación
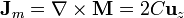
Resultan corrientes que suben axialmente por el cilindro.
2.2 Superficiales
Las corrientes de magnetización en una interfaz entre dos regiones tienen la forma general
![\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]\,](/wiki/images/math/e/5/6/e5696e953c72cfdd30df07674308cb82.png)
que, para el caso de que una de las dos regiones sea el vacío, se reduce a
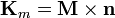
siendo  la normal exterior al volumen imanado. En nuestro caso, tenemos
la normal exterior al volumen imanado. En nuestro caso, tenemos
- En la base superior
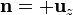 y
y
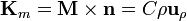
- En la base inferior
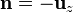 y
y

- En la cara lateral
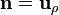
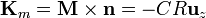
Nótese que deben sustituirse las coordenadas por su valor en la superficie. En los dos primeros casos, ρ varía desde 0 a R, por lo que se deja como variable, pero para la cara lateral posee un valor constante ρ = R, que debe sustituirse.
Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación.
3 Cargas magnéticas
Las densidades de carga magnética equivalentes a esta magnetización pueden también ser de volumen o superficiales.
3.1 De volumen
En el exterior del cilindro la densidad es nula, por serlo la imanación.

En el interior la densidad de carga también es nula, por ser este campo solenoidal
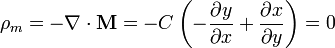
3.2 De superficie
Como en el caso de las corrientes de imanación, tenemos posibles densidades de carga magnética en las bases y en la cara lateral. La expresión general de las cargas magnéticas en una interfaz es
![\sigma_m = -\mathbf{n}\cdot[\mathbf{M}]\,](/wiki/images/math/7/2/b/72bf515f4c6a685761a96223ab5df3c9.png)
que, para el caso de que una de las dos regiones sea el vacío, se reduce a
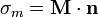
En nuestro caso, tenemos
- En la base superior
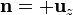 y
y

- En la base inferior
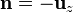 y
y
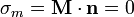
- En la cara lateral
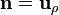
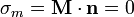
En las tres superficies la imanación es perpendicular al vector normal, por ser la imanación acimutal.
4 Campos magnéticos
Podemos hallar los campos magnéticos a partir de las corrientes de imanación. Así calcularíamos  y luego
y luego  .
.
Sin embargo es mucho más sencillo hallar primero  , cuyas fuentes son las corrientes libres y las cargas magnéticas, y a partir de ahí calcular
, cuyas fuentes son las corrientes libres y las cargas magnéticas, y a partir de ahí calcular  . La razón es obvia: tanto las corrientes libres como las cargas magnéticas son nulas.
. La razón es obvia: tanto las corrientes libres como las cargas magnéticas son nulas.
Las ecuaciones generales para el campo  son
son
![\begin{matrix}\nabla\cdot\mathbf{H}=\rho_m & \qquad & \mathbf{n}\cdot[\mathbf{H}]=\sigma_m \\ & & \\
\nabla\times\mathbf{H}=\mathbf{J}_l & \qquad & \mathbf{n}\times[\mathbf{H}]=\mathbf{K}_l \end{matrix}](/wiki/images/math/b/2/1/b212d42a70e6142e22c141f0830a2ed8.png)
En este problema, en el que solo tenemos un material imanado y no hay aplicada ninguna corriente libre de origen externo, las corrientes libres son nulas
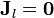

Asimismo, hemos calculado en el apartado anterior que las densidades de carga magnética son nulas, tanto en el volumen, como en las interfaces
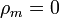

Además, por ser el sistema de tamaño finito, el campo magnético que produce tiende a cero en puntos alejados

Según esto, el campo magnético  carece de fuentes escalares y vectoriales y decae en el infinito. Por tanto, el campo
carece de fuentes escalares y vectoriales y decae en el infinito. Por tanto, el campo  es nulo en todo el espacio:
es nulo en todo el espacio:
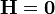
y, una vez que tenemos el campo  tenemos el campo
tenemos el campo 






