Problemas de inducción electromagnética (GIA)
De Laplace
(→Inducción en espira rectangular móvil con voltímetro) |
|||
| (23 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | ==[[ | + | ==[[Ley_de_Lenz_en_espira_con_barra_móvil_(F2GIA)|Ley de Lenz en espira con barra móvil]]== |
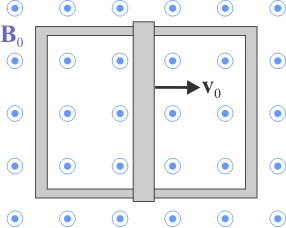
| - | [[Archivo: | + | [[Archivo:Ley_de_Lenz_0.gif|right]]Una espira conductora rectangular fija se halla inmersa en un campo magnético uniforme y constante de magnitud <math>B_0</math>, y dirección perpendicular al plano de la espira. Un barra conductora se desplaza con velocidad uniforme <math>v_0</math>, manteniendo sus extremos en contacto con sendos lados paralelos de la espira. Indique los sentidos con que las corrientes eléctricas inducidas recorren cada una de mallas en que queda dividida la espira |
| + | |||
| + | | ||
| + | |||
| + | | ||
| + | |||
| + | ==[[Intensidad_de_corriente_en_lector_magnético,_F2_GIA_(Jun,_2013)|Intensidad de corriente en lector magnético]]== | ||
| + | |||
| + | |||
| + | Para implementar un lector de cinta magnética se utiliza una espira cuadrada conductora. Ésta se halla conectada a un amperímetro que mide la intensidad inducida cuando bajo ella pasa una cinta en la cuál hay una secuencia de regiones magnetizadas y no magnetizadas. Aquéllas producen un campo magnético <math>\mathbf{B}</math>, que puede considerarse localizado en dichas regiones y prácticamente uniforme en las proximidades de la cinta, siendo su dirección perpendicular al plano de la espira lectora. El amperímetro está conectado de manera que mide valores positivos de intensidad cuando la corriente inducida | ||
| + | recorre la espira lectora en sentido antihorario, teniendo ésta un tamaño algo menor que las secciones magnetizadas. Si la cinta se desplaza con velocidad constante <math>\mathbf{v}_0</math> respecto de la espira lectora fija, cómo es la corriente inducida en la espira cuando bajo ella pasa una sección magnetizada en sentido negativo (ver figura). | ||
| + | |||
| + | <center>[[Archivo:lector_magnet_1.gif]]</center> | ||
| - | |||
| - | |||
==[[Espira_en_el_interior_de_un_solenoide_(F2GIA)| Espira cuadrada en el interior de un solenoide]]== | ==[[Espira_en_el_interior_de_un_solenoide_(F2GIA)| Espira cuadrada en el interior de un solenoide]]== | ||
| Línea 11: | Línea 21: | ||
| | ||
| + | |||
| + | ==[[Tensión_inducida_en_espira,_F2_GIA_(Jun,_2013)|Tensión inducida en una espira abierta]]== | ||
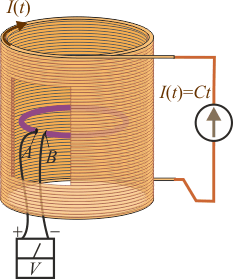
| + | [[Archivo:tension_inducida_0.gif|right]]Un solenoide recto de forma cilíndrica y longitud <math>l</math>, mucho mayor que su radio, está formado por <math>N</math> espiras distribuidas de forma compacta que son recorridas en sentido horario por una corriente eléctrica que crece linealmente según la ley <math>I(t)=C\!\ t</math> (<math>C</math>, constante). En un plano paralelo a las espiras del solenoide y en el interior de éste, se encuentra una pequeña espira circular de radio <math>a</math>, menor que el del solenoide. Si a la espira le falta un pequeño trozo, de manera que constituye un circuito abierto, ¿cómo es la tensión <math>V=V_A-V_B</math> que mediría un voltímetro conectado a sus extremos, tal como se indica en la figura? | ||
| + | |||
| + | | ||
| + | |||
| + | | ||
| + | |||
| + | ==[[Circuito_eléctrico_con_bombilla_móvil,_F2_GIA_(Jun,_2015)|Circuito eléctrico con bombilla móvil]]== | ||
| + | |||
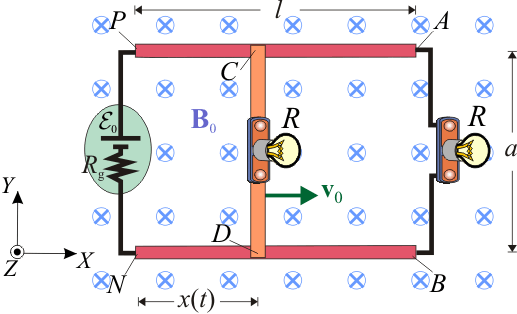
| + | El circuito eléctrico de la figura está formado por dos regletas conductoras, ambas de longitud <math>l</math>, dispuestas en paralelo y separadas por una distancia fija <math>a</math>. Sendos extremos de dichas regletas están conectados a los electrodos <math>P</math> y <math>N</math> de un generador | ||
| + | d.c. (batería), cuya f.e.m. tiene un valor constante <math>\mathcal{E}_0</math> y una resistencia interna <math>R_\mathrm{g}</math>. Los otros extremos de las dos regletas, <math>A</math> y <math>B</math>, se conectan a través de una bombilla incandescente de resistencia <math>R</math>. Además, se tienen otros dos segmentos conductores, alineados y conectados por otra bombilla idéntica a la anterior, y con los extremos libres, <math>C</math> y <math>D</math>, siempre en contacto con las regletas. El resto de resistencias eléctricas del sistema son despreciables frente al valor <math>R</math> de las bombillas, excepto la resistencia interna del generador, que vale <math>R_\mathrm{g}=R/2</math>. Todo el sistema está sometido a un campo magnético uniforme <math>\mathbf{B}_0=-B_0\!\ \mathbf{k}</math> perpendicular al plano <math>OXY</math> que contiene al circuito, y de sentido opuesto al eje | ||
| + | <math>OZ</math>, tal como se indica en la figura. | ||
| + | |||
| + | Inicialmente, la rama conductora <math>CD</math> está en reposo, en contacto con los extremos de las regletas que se hallan conectados a la batería (<math>P</math> y <math>N</math>). En esta situación, obtenga las expresiones de las siguientes magnitudes en función de los parámetros indicados en el | ||
| + | enunciado (*): | ||
| + | |||
| + | ; | ||
| + | : a) Intensidad de corriente total suministrada por el generador, e intensidades en cada una de las ramas. | ||
| + | : b) Expresión de la energía que por unidad de tiempo se disipa en cada resistencia. ¿Cómo serán, comparativamente, las intensidades luminosas de las bombillas? | ||
| + | |||
| + | [[Archivo:FII_1aconv_14_15_P2_0.gif|right]] A partir de un cierto instante, la rama <math>CD</math> con bombilla incluida, se desplaza hacia la bombilla fija que cierra el circuito entre <math>A</math> y <math>B</math>, manteniéndose perpendicular a las regletas conductoras y alcanzando una velocidad constante de valor <math>v_0</math>. En esta nueva situación, obtenga las expresiones de: | ||
| + | |||
| + | ; | ||
| + | : c) Flujos magnéticos a través de las espiras <math>\partial \Sigma_1\equiv PABN</math> y <math>\partial \Sigma_2\equiv PCDN</math>, y fuerzas electromotrices inducidas en cada una de ellas. | ||
| + | : d) Ecuaciones del circuito en las espiras <math>\partial \Sigma_1</math> y <math>\partial \Sigma_2</math>. | ||
| + | : e) Intensidades de las corrientes eléctricas que recorren el generador y cada una de las dos bombillas. ¿Podría llegar a apagarse alguna de ellas? | ||
| + | |||
| + | (*)Los apartados (a) y (b) corresponden al tema "4. Corrientes eléctricas" | ||
| + | |||
| + | ==[[Inducción_en_espira_rectangular_móvil_con_voltímetro_(F2GIA)|Inducción en espira rectangular móvil con voltímetro]]== | ||
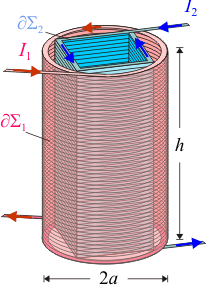
| + | Una espira rectangular <math>ABCD</math> está formada por cuatro conductores filiformes de igual resistividad y sección, y de longitudes <math>a</math> y <math>2a</math>, siendo <math>R</math> su resistencia eléctrica total. En el lado corto <math>AB</math> tiene incrustado un generador eléctrico ideal con una f.e.m. constante <math>\mathcal{E}_0</math>, y con sus electrodos conectados de manera que, por sí sola, generaría una corriente eléctrica que recorrería la espira en sentido horario. Además, en los puntos medios de los lados largos, <math>BC</math> y <math>DA</math>, se conectan sendos conductores filiformes rectilíneos de resistencia nula, paralelos a los lados cortos y que terminan en los extremos <math>E</math> y <math>F</math>, muy próximos pero con una pequeña separación entre ellos, que hace que está rama del circuito esté abierta. | ||
| + | ; | ||
| + | La espira se encuentra siempre contenida en el plano <math>OXY</math>, con sus lados cortos <math>AB</math> y <math>CD</math> paralelos al eje <math>OY</math>, y se desplaza con velocidad constante <math>\vec{v}_0=v_0\!\ \vec{\imath}</math>, con <math>v_0=a/T</math>. Inicialmente, la espira se encuentra en una región donde no existe campo magnético, pero a partir del instante que consideramos <math>t=0</math>, la espira penetra por su lado corto <math>CD</math> en una región donde existe un campo magnético uniforme <math>\vec{B}_0=-B_0\!\ \vec{k}</math>, cuya intensidad se ajusta de manera que se cumpla <math>B_0\!\ a\!\ v_0=\mathcal{E}_0</math>. | ||
| + | ; | ||
| + | : '''(a)''' Para los instantes anteriores a que la espira entre en la región de campo magnético (<math>t<0</math>), determine el valor de la intensidad <math>I</math> (medida en sentido horario) de la corriente eléctrica que recorre la espira. Calcule también el valor del voltaje <math>V</math> entre los extremos <math>E</math> y <math>F</math>. | ||
| + | : '''(b)''' En los instantes de tiempo <math>t>0</math>, ¿cómo es la señal de intensidad <math>I(t)</math> de la corriente eléctrica que recorre la espira? ¿Y la señal de voltaje <math>V(t)</math> entre los extremos abiertos <math>E</math> y <math>F</math>? | ||
| + | : '''(c)''' Si se repite el experimento pero conectando los extremos <math>E</math> y <math>F</math> mediante un amperímetro de resistencia nula, ¿cómo sería la señal de intensidad de corriente <math>i (t)</math> que registraría dicho amperímetro en los intervalos de tiempo <math>t<0</math> y <math>t>0</math>? | ||
| + | <center>[[Archivo:FII_gIA_1acon_18_19_pr.png]]</center> | ||
==[[Voltaje_inducido_en_espira_alrededor_de_un_solenoide_(F2GIA)|Voltaje inducido en espira alrededor de un solenoide]]== | ==[[Voltaje_inducido_en_espira_alrededor_de_un_solenoide_(F2GIA)|Voltaje inducido en espira alrededor de un solenoide]]== | ||
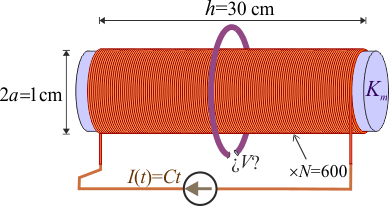
[[Archivo:espira_sole_ferro_0.gif|right]]Un solenoide de longitud <math>h=30\,\mathrm{cm}</math> y diámetro <math>2a=1\,\mathrm{cm}</math>, está formado por <math>N=600</math> espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es <math>K_m\approx 5000</math>. Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley <math>I(t) = C t</math>, con <math>C=10\,\mathrm{mA/s}</math>. ¿Qué tensión se medirá entre los extremos abiertos de la anilla? | [[Archivo:espira_sole_ferro_0.gif|right]]Un solenoide de longitud <math>h=30\,\mathrm{cm}</math> y diámetro <math>2a=1\,\mathrm{cm}</math>, está formado por <math>N=600</math> espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es <math>K_m\approx 5000</math>. Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley <math>I(t) = C t</math>, con <math>C=10\,\mathrm{mA/s}</math>. ¿Qué tensión se medirá entre los extremos abiertos de la anilla? | ||
| - | ==[[ | + | |
| - | [[Archivo: | + | ==[[Bobina cortocircuitada sometida a campo externo (F2GIA)|Bobina cortocircuitada sometida a campo externo]]== |
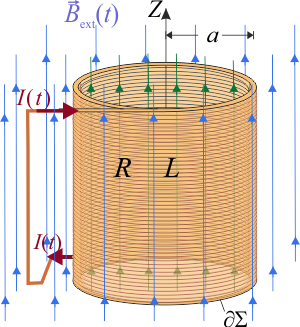
| + | [[Archivo:f2_gIA_ex1ac_17_18_e7_00.png|right]]Una bobina <math>\partial\Sigma</math> de resistencia eléctrica <math>\displaystyle R</math> y autoinducción <math>\displaystyle L</math> está formada por ''N'' espiras idénticas de radio <math>\displaystyle a</math>, todas perpendiculares al eje <math>OZ</math> que pasa por sus centros. La espira está cortocircuitada y sometida a un campo magnético externo uniforme y variable en el tiempo <math>\vec{B}_\mathrm{ext}(t)=B(t)\!\ \vec{k}</math>. El resultado es que la bobina es recorrida por una intensidad de corriente <math>\displaystyle I(t)</math> medida en el sentido antihorario. | ||
| + | |||
| + | # Obtenga la expresión del flujo magnético total a través de las <math>N</math> espiras que forman la bobina (no olvidar que su autoinducción tiene un valor apreciable). | ||
| + | # Aplique las leyes de la inducción electromagnética para determinar cómo deber ser la ley horaria <math>\displaystyle B(t)</math> que verifica el campo magnético externo para que la bobina sea recorrida por una corriente eléctrica de intensidad constante, <math>I_0</math>. | ||
| + | # En las condiciones del apartado anterior, ¿qué energía magnética se almacena en la bobina? ¿Qué cantidad de energía por unidad de tiempo se disipa en la bobina por efecto Joule? | ||
| + | |||
| + | ==[[Coeficientes_de_inducción_de_dos_bobinas_(F2GIA)|Coeficientes de inducción en sistema de dos bobinas]]== | ||
| + | [[Archivo:coef_inducc_0.gif|right]]Se tienen dos bobinas o solenoides, ambas de igual longitud <math>h</math>, pero de distinta sección: la bobina “1” tiene forma de cilindro recto, estando formada por <math>N_1</math> espiras circulares de radio <math>a</math>. Por su parte, la bobina “2” tiene forma de prisma recto de sección cuadrada y la constituyen <math>N_2</math> espiras cuadradas iguales, cuya diagonal mide <math>2a</math>. En ambas bobinas los hilos conductores están enrollados en el mismo sentido, y de manera que las espiras se distribuyen de forma compacta en planos perpendiculares a su correspondiente eje. Asumiendo que se verifica la condición de bobinas largas (<math>h\gg 2a</math>), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”? | ||
| + | |||
| + | | ||
| + | |||
| + | | ||
| + | |||
| + | ==[[Inducción_en_barra_y_escuadra,_F2_GIA_(Jun,_2013)|Inducción en barra y escuadra conductoras]]== | ||
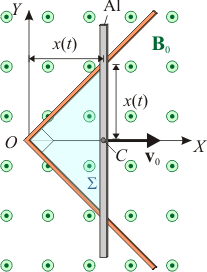
| + | [[Archivo:induc_barra_escuadra_0.gif|right]]Dos conductores rectilíneos filiformes de resistencia despreciable, están contenidos en el plano <math>OXY</math>, conectados en ángulo recto en el punto <math>O</math>, y de manera que el eje <math>OX</math> coincide con la bisectriz del ángulo recto que forman los hilos conductores. Un barra de aluminio, de sección <math>S</math> y longitud <math>a</math>, se mueve manteniéndose siempre perpendicular al eje <math>OX</math>, y en contacto con los conductores filiformes. El movimiento de la barra es tal que partiendo del punto <math>O</math>, su centro <math>C</math> se desplaza con velocidad constante <math>v_0</math> en el sentido positivo del eje. Todo el sistema está sometido a un campo magnético uniforme y constante, <math>\mathbf{B}_0=B_0\!\ \mathbf{k}</math>. | ||
| + | |||
| + | # Obtenga la expresión que describe cómo varía en el tiempo el flujo magnético a través de la espira <math>\partial\Sigma</math> formada por los conductores filiformes y la barra (considérese despreciable la autoinducción de la espira). Obtenga también la fuerza electromotriz inducida en dicho circuito. | ||
| + | # Determine la expresión de la intensidad de corriente eléctrica inducida, indicando el sentido en que recorre la espira. Asimismo, obtenga las expresiones de la potencia disipada por efecto Joule en la barra, y del calor total generado desde que ésta empieza a moverse hasta que pierde el contacto con los conductores filiformes. | ||
| + | # Obtenga la fuerza magnética (magnitud vectorial) que actúa sobre la corriente en la barra móvil, en función de su posición. | ||
| + | # Sabiendo que la conductividad del aluminio es <math>\sigma_{{}_\mathrm{Al}}=37.7\times10^{6}\,\mathrm{S}/\mathrm{m}</math>, calcule el valor de la intensidad de corriente, el calor generado por efecto Joule en la barra y el valor máximo de la fuerza magnética que actúa sobre ella, para el caso: <math>B_0=0.1\,\mathrm{T}</math>; <math>v_0=1\,\mathrm{cm}/\mathrm{s}</math>; <math>S=79.6\,\mathrm{mm}^2</math>; <math>a=1\,\mathrm{m}</math>. | ||
| + | |||
| + | ==[[Circuito_variable_en_plano_inclinado_(F2GIA)|Circuito variable en un plano inclinado, sometido a campo magnético]]== | ||
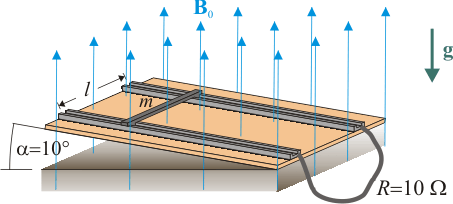
| + | [[Archivo:bol_6_ej_4_0.gif|right]]Una varilla conductora de masa <math>m=2.0\,\mathrm{kg}\,</math> se deja caer deslizando sin rozamiento por dos guías metálicas paralelas separadas una distancia <math>l=5.0\,\mathrm{m}\,</math> contenidas en un plano inclinado que forma un ángulo <math>\alpha=10^o</math> con la horizontal. La dirección de la varilla es, en todo instante, perpendicular a las guías, las cuáles tienen conectados sus extremos mediante un cable de resistencia eléctrica <math>R=10\,\Omega</math>, que cierra el circuito. Las resistencias eléctricas de la varilla y las guías son despreciables. El sistema descrito se halla inmerso en un campo magnético uniforme y constante, <math>\mathbf{B}_0</math>, de <math>0.5\,\mathrm{T}\,</math> de intensidad, aplicado en dirección vertical y sentido contrario a la gravedad. Calcule: | ||
| + | |||
| + | # Corriente inducida en el circuito y velocidad límite que alcanzará la varilla. | ||
| + | # Potencia disipada por efecto Joule en la resistencia. Compare esta potencia con el trabajo que por unidad de tiempo realiza la fuerza peso sobre la varilla. | ||
[[Categoría:Problemas de inducción electromagnética F2 GIA]] | [[Categoría:Problemas de inducción electromagnética F2 GIA]] | ||
última version al 19:06 31 jul 2019
1 Ley de Lenz en espira con barra móvil
Una espira conductora rectangular fija se halla inmersa en un campo magnético uniforme y constante de magnitud B0, y dirección perpendicular al plano de la espira. Un barra conductora se desplaza con velocidad uniforme v0, manteniendo sus extremos en contacto con sendos lados paralelos de la espira. Indique los sentidos con que las corrientes eléctricas inducidas recorren cada una de mallas en que queda dividida la espira
2 Intensidad de corriente en lector magnético
Para implementar un lector de cinta magnética se utiliza una espira cuadrada conductora. Ésta se halla conectada a un amperímetro que mide la intensidad inducida cuando bajo ella pasa una cinta en la cuál hay una secuencia de regiones magnetizadas y no magnetizadas. Aquéllas producen un campo magnético  , que puede considerarse localizado en dichas regiones y prácticamente uniforme en las proximidades de la cinta, siendo su dirección perpendicular al plano de la espira lectora. El amperímetro está conectado de manera que mide valores positivos de intensidad cuando la corriente inducida
recorre la espira lectora en sentido antihorario, teniendo ésta un tamaño algo menor que las secciones magnetizadas. Si la cinta se desplaza con velocidad constante
, que puede considerarse localizado en dichas regiones y prácticamente uniforme en las proximidades de la cinta, siendo su dirección perpendicular al plano de la espira lectora. El amperímetro está conectado de manera que mide valores positivos de intensidad cuando la corriente inducida
recorre la espira lectora en sentido antihorario, teniendo ésta un tamaño algo menor que las secciones magnetizadas. Si la cinta se desplaza con velocidad constante 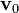 respecto de la espira lectora fija, cómo es la corriente inducida en la espira cuando bajo ella pasa una sección magnetizada en sentido negativo (ver figura).
respecto de la espira lectora fija, cómo es la corriente inducida en la espira cuando bajo ella pasa una sección magnetizada en sentido negativo (ver figura).
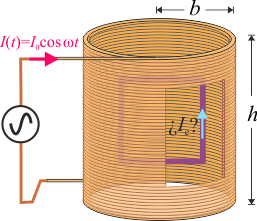
3 Espira cuadrada en el interior de un solenoide
Un solenoide constituido por N espiras compactas paralelas, con forma de cilindro recto de longitud h mucho mayor que su radio b, es recorrido por una corriente eléctrica de intensidad variable en el tiempo según la ley I(t) = I0cos(ωt), siendo I0 y ω constantes conocidas. En el interior del solenoide hay una pequeña espira cuadrada de resistencia eléctrica R, autoinducción despreciable y lado a, menor que el radio b. Esta espira esté contenida en un plano perpendicular a las espiras del solenoide. ¿Cuál es el valor de la intensidad de corriente Ie que recorre la espira cuadrada?
4 Tensión inducida en una espira abierta
Un solenoide recto de forma cilíndrica y longitud l, mucho mayor que su radio, está formado por N espiras distribuidas de forma compacta que son recorridas en sentido horario por una corriente eléctrica que crece linealmente según la ley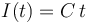 (C, constante). En un plano paralelo a las espiras del solenoide y en el interior de éste, se encuentra una pequeña espira circular de radio a, menor que el del solenoide. Si a la espira le falta un pequeño trozo, de manera que constituye un circuito abierto, ¿cómo es la tensión V = VA − VB que mediría un voltímetro conectado a sus extremos, tal como se indica en la figura?
(C, constante). En un plano paralelo a las espiras del solenoide y en el interior de éste, se encuentra una pequeña espira circular de radio a, menor que el del solenoide. Si a la espira le falta un pequeño trozo, de manera que constituye un circuito abierto, ¿cómo es la tensión V = VA − VB que mediría un voltímetro conectado a sus extremos, tal como se indica en la figura?
5 Circuito eléctrico con bombilla móvil
El circuito eléctrico de la figura está formado por dos regletas conductoras, ambas de longitud l, dispuestas en paralelo y separadas por una distancia fija a. Sendos extremos de dichas regletas están conectados a los electrodos P y N de un generador
d.c. (batería), cuya f.e.m. tiene un valor constante 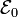 y una resistencia interna Rg. Los otros extremos de las dos regletas, A y B, se conectan a través de una bombilla incandescente de resistencia R. Además, se tienen otros dos segmentos conductores, alineados y conectados por otra bombilla idéntica a la anterior, y con los extremos libres, C y D, siempre en contacto con las regletas. El resto de resistencias eléctricas del sistema son despreciables frente al valor R de las bombillas, excepto la resistencia interna del generador, que vale Rg = R / 2. Todo el sistema está sometido a un campo magnético uniforme
y una resistencia interna Rg. Los otros extremos de las dos regletas, A y B, se conectan a través de una bombilla incandescente de resistencia R. Además, se tienen otros dos segmentos conductores, alineados y conectados por otra bombilla idéntica a la anterior, y con los extremos libres, C y D, siempre en contacto con las regletas. El resto de resistencias eléctricas del sistema son despreciables frente al valor R de las bombillas, excepto la resistencia interna del generador, que vale Rg = R / 2. Todo el sistema está sometido a un campo magnético uniforme 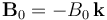 perpendicular al plano OXY que contiene al circuito, y de sentido opuesto al eje
OZ, tal como se indica en la figura.
perpendicular al plano OXY que contiene al circuito, y de sentido opuesto al eje
OZ, tal como se indica en la figura.
Inicialmente, la rama conductora CD está en reposo, en contacto con los extremos de las regletas que se hallan conectados a la batería (P y N). En esta situación, obtenga las expresiones de las siguientes magnitudes en función de los parámetros indicados en el enunciado (*):
- a) Intensidad de corriente total suministrada por el generador, e intensidades en cada una de las ramas.
- b) Expresión de la energía que por unidad de tiempo se disipa en cada resistencia. ¿Cómo serán, comparativamente, las intensidades luminosas de las bombillas?
- c) Flujos magnéticos a través de las espiras
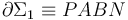 y
y 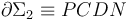 , y fuerzas electromotrices inducidas en cada una de ellas.
, y fuerzas electromotrices inducidas en cada una de ellas.
- d) Ecuaciones del circuito en las espiras
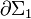 y
y 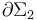 .
.
- e) Intensidades de las corrientes eléctricas que recorren el generador y cada una de las dos bombillas. ¿Podría llegar a apagarse alguna de ellas?
(*)Los apartados (a) y (b) corresponden al tema "4. Corrientes eléctricas"
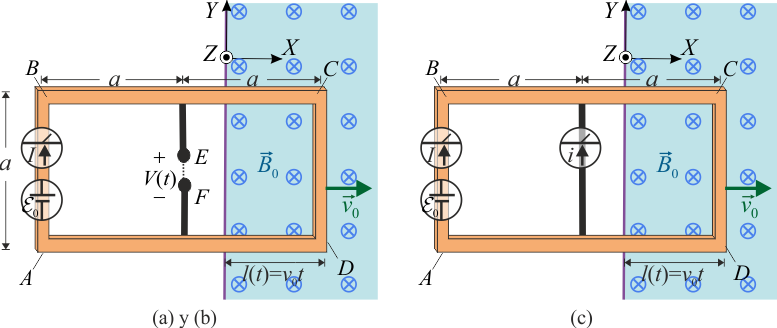
6 Inducción en espira rectangular móvil con voltímetro
Una espira rectangular ABCD está formada por cuatro conductores filiformes de igual resistividad y sección, y de longitudes a y 2a, siendo R su resistencia eléctrica total. En el lado corto AB tiene incrustado un generador eléctrico ideal con una f.e.m. constante 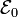 , y con sus electrodos conectados de manera que, por sí sola, generaría una corriente eléctrica que recorrería la espira en sentido horario. Además, en los puntos medios de los lados largos, BC y DA, se conectan sendos conductores filiformes rectilíneos de resistencia nula, paralelos a los lados cortos y que terminan en los extremos E y F, muy próximos pero con una pequeña separación entre ellos, que hace que está rama del circuito esté abierta.
, y con sus electrodos conectados de manera que, por sí sola, generaría una corriente eléctrica que recorrería la espira en sentido horario. Además, en los puntos medios de los lados largos, BC y DA, se conectan sendos conductores filiformes rectilíneos de resistencia nula, paralelos a los lados cortos y que terminan en los extremos E y F, muy próximos pero con una pequeña separación entre ellos, que hace que está rama del circuito esté abierta.
La espira se encuentra siempre contenida en el plano OXY, con sus lados cortos AB y CD paralelos al eje OY, y se desplaza con velocidad constante 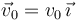 , con v0 = a / T. Inicialmente, la espira se encuentra en una región donde no existe campo magnético, pero a partir del instante que consideramos t = 0, la espira penetra por su lado corto CD en una región donde existe un campo magnético uniforme
, con v0 = a / T. Inicialmente, la espira se encuentra en una región donde no existe campo magnético, pero a partir del instante que consideramos t = 0, la espira penetra por su lado corto CD en una región donde existe un campo magnético uniforme 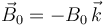 , cuya intensidad se ajusta de manera que se cumpla
, cuya intensidad se ajusta de manera que se cumpla 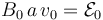 .
.
- (a) Para los instantes anteriores a que la espira entre en la región de campo magnético (t < 0), determine el valor de la intensidad I (medida en sentido horario) de la corriente eléctrica que recorre la espira. Calcule también el valor del voltaje V entre los extremos E y F.
- (b) En los instantes de tiempo t > 0, ¿cómo es la señal de intensidad I(t) de la corriente eléctrica que recorre la espira? ¿Y la señal de voltaje V(t) entre los extremos abiertos E y F?
- (c) Si se repite el experimento pero conectando los extremos E y F mediante un amperímetro de resistencia nula, ¿cómo sería la señal de intensidad de corriente i(t) que registraría dicho amperímetro en los intervalos de tiempo t < 0 y t > 0?
7 Voltaje inducido en espira alrededor de un solenoide
Un solenoide de longitud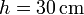 y diámetro
y diámetro 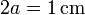 , está formado por N = 600 espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es
, está formado por N = 600 espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es 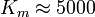 . Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley I(t) = Ct, con
. Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley I(t) = Ct, con 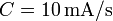 . ¿Qué tensión se medirá entre los extremos abiertos de la anilla?
. ¿Qué tensión se medirá entre los extremos abiertos de la anilla?
8 Bobina cortocircuitada sometida a campo externo
Una bobina de resistencia eléctrica
de resistencia eléctrica 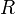 y autoinducción
y autoinducción 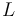 está formada por N espiras idénticas de radio
está formada por N espiras idénticas de radio 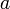 , todas perpendiculares al eje OZ que pasa por sus centros. La espira está cortocircuitada y sometida a un campo magnético externo uniforme y variable en el tiempo
, todas perpendiculares al eje OZ que pasa por sus centros. La espira está cortocircuitada y sometida a un campo magnético externo uniforme y variable en el tiempo 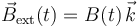 . El resultado es que la bobina es recorrida por una intensidad de corriente
. El resultado es que la bobina es recorrida por una intensidad de corriente 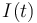 medida en el sentido antihorario.
medida en el sentido antihorario.
- Obtenga la expresión del flujo magnético total a través de las N espiras que forman la bobina (no olvidar que su autoinducción tiene un valor apreciable).
- Aplique las leyes de la inducción electromagnética para determinar cómo deber ser la ley horaria
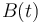 que verifica el campo magnético externo para que la bobina sea recorrida por una corriente eléctrica de intensidad constante, I0.
que verifica el campo magnético externo para que la bobina sea recorrida por una corriente eléctrica de intensidad constante, I0.
- En las condiciones del apartado anterior, ¿qué energía magnética se almacena en la bobina? ¿Qué cantidad de energía por unidad de tiempo se disipa en la bobina por efecto Joule?
9 Coeficientes de inducción en sistema de dos bobinas
Se tienen dos bobinas o solenoides, ambas de igual longitud h, pero de distinta sección: la bobina “1” tiene forma de cilindro recto, estando formada por N1 espiras circulares de radio a. Por su parte, la bobina “2” tiene forma de prisma recto de sección cuadrada y la constituyen N2 espiras cuadradas iguales, cuya diagonal mide 2a. En ambas bobinas los hilos conductores están enrollados en el mismo sentido, y de manera que las espiras se distribuyen de forma compacta en planos perpendiculares a su correspondiente eje. Asumiendo que se verifica la condición de bobinas largas (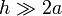 ), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”?
), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”?
10 Inducción en barra y escuadra conductoras
Dos conductores rectilíneos filiformes de resistencia despreciable, están contenidos en el plano OXY, conectados en ángulo recto en el punto O, y de manera que el eje OX coincide con la bisectriz del ángulo recto que forman los hilos conductores. Un barra de aluminio, de sección S y longitud a, se mueve manteniéndose siempre perpendicular al eje OX, y en contacto con los conductores filiformes. El movimiento de la barra es tal que partiendo del punto O, su centro C se desplaza con velocidad constante v0 en el sentido positivo del eje. Todo el sistema está sometido a un campo magnético uniforme y constante,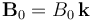 .
.
- Obtenga la expresión que describe cómo varía en el tiempo el flujo magnético a través de la espira
 formada por los conductores filiformes y la barra (considérese despreciable la autoinducción de la espira). Obtenga también la fuerza electromotriz inducida en dicho circuito.
formada por los conductores filiformes y la barra (considérese despreciable la autoinducción de la espira). Obtenga también la fuerza electromotriz inducida en dicho circuito.
- Determine la expresión de la intensidad de corriente eléctrica inducida, indicando el sentido en que recorre la espira. Asimismo, obtenga las expresiones de la potencia disipada por efecto Joule en la barra, y del calor total generado desde que ésta empieza a moverse hasta que pierde el contacto con los conductores filiformes.
- Obtenga la fuerza magnética (magnitud vectorial) que actúa sobre la corriente en la barra móvil, en función de su posición.
- Sabiendo que la conductividad del aluminio es
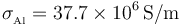 , calcule el valor de la intensidad de corriente, el calor generado por efecto Joule en la barra y el valor máximo de la fuerza magnética que actúa sobre ella, para el caso:
, calcule el valor de la intensidad de corriente, el calor generado por efecto Joule en la barra y el valor máximo de la fuerza magnética que actúa sobre ella, para el caso: 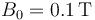 ;
; 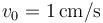 ;
; 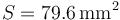 ;
; 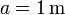 .
.
11 Circuito variable en un plano inclinado, sometido a campo magnético
Una varilla conductora de masa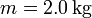 se deja caer deslizando sin rozamiento por dos guías metálicas paralelas separadas una distancia
se deja caer deslizando sin rozamiento por dos guías metálicas paralelas separadas una distancia 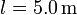 contenidas en un plano inclinado que forma un ángulo α = 10o con la horizontal. La dirección de la varilla es, en todo instante, perpendicular a las guías, las cuáles tienen conectados sus extremos mediante un cable de resistencia eléctrica
contenidas en un plano inclinado que forma un ángulo α = 10o con la horizontal. La dirección de la varilla es, en todo instante, perpendicular a las guías, las cuáles tienen conectados sus extremos mediante un cable de resistencia eléctrica 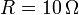 , que cierra el circuito. Las resistencias eléctricas de la varilla y las guías son despreciables. El sistema descrito se halla inmerso en un campo magnético uniforme y constante,
, que cierra el circuito. Las resistencias eléctricas de la varilla y las guías son despreciables. El sistema descrito se halla inmerso en un campo magnético uniforme y constante,  , de
, de 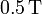 de intensidad, aplicado en dirección vertical y sentido contrario a la gravedad. Calcule:
de intensidad, aplicado en dirección vertical y sentido contrario a la gravedad. Calcule:
- Corriente inducida en el circuito y velocidad límite que alcanzará la varilla.
- Potencia disipada por efecto Joule en la resistencia. Compare esta potencia con el trabajo que por unidad de tiempo realiza la fuerza peso sobre la varilla.