Inducción en barra y escuadra, F2 GIA (Jun, 2013)
De Laplace
Contenido |
1 Enunciado
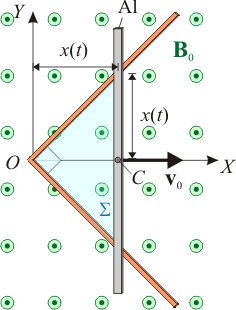
Dos conductores rectilíneos filiformes de resistencia despreciable, están contenidos en el plano OXY, conectados en ángulo recto en el punto O, y de manera que el eje OX coincide con la bisectriz del ángulo recto que forman los hilos conductores. Un barra de aluminio, de sección S y longitud a, se mueve manteniéndose siempre perpendicular al eje OX, y en contacto con los conductores filiformes. El movimiento de la barra es tal que partiendo del punto O, su centro C se desplaza con velocidad constante v0 en el sentido positivo del eje. Todo el sistema está sometido a un campo magnético uniforme y constante,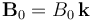 .
.
- Obtenga la expresión que describe cómo varía en el tiempo el flujo magnético a través de la espira
 formada por los conductores filiformes y la barra (considérese despreciable la autoinducción de la espira). Obtenga también la fuerza electromotriz inducida en dicho circuito.
formada por los conductores filiformes y la barra (considérese despreciable la autoinducción de la espira). Obtenga también la fuerza electromotriz inducida en dicho circuito.
- Determine la expresión de la intensidad de corriente eléctrica inducida, indicando el sentido en que recorre la espira. Asimismo, obtenga las expresiones de la potencia disipada por efecto Joule en la barra, y del calor total generado desde que ésta empieza a moverse hasta que pierde el contacto con los conductores filiformes.
- Obtenga la fuerza magnética (magnitud vectorial) que actúa sobre la corriente en la barra móvil, en función de su posición.
- Sabiendo que la conductividad del aluminio es
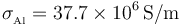 , calcule el valor de la intensidad de corriente, el calor generado por efecto Joule en la barra y el valor máximo de la fuerza magnética que actúa sobre ella, para el caso:
, calcule el valor de la intensidad de corriente, el calor generado por efecto Joule en la barra y el valor máximo de la fuerza magnética que actúa sobre ella, para el caso: 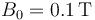 ;
; 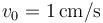 ;
; 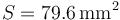 ;
; 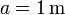 .
.
2 Solución
2.1 Flujo magnético y fuerza electromotriz inducida
2.1.1 Flujo magnético a través de la espira
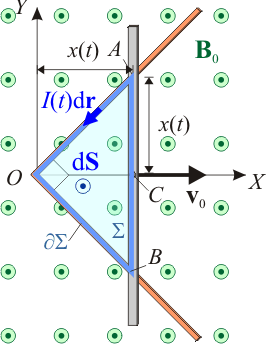
La barra de aluminio y la escuadra de conductores filiformes forman una espira triangular  , contenida en todo instante en el plano OXY, y cuyos vértices son el vértice O de la escuadra y los puntos A y B donde se verifica el contacto de ésta con la barra móvil. Puesto que la barra se desplaza con velocidad constante respecto de la escuadra, la superficie delimitada por la espira varía en el tiempo, Σ(t). Consideremos un instante arbitrario, t, en el cuál la barra se encuentra a una distancia x(t) del vértice O, y calculemos el flujo del campo magnético uniforme
, contenida en todo instante en el plano OXY, y cuyos vértices son el vértice O de la escuadra y los puntos A y B donde se verifica el contacto de ésta con la barra móvil. Puesto que la barra se desplaza con velocidad constante respecto de la escuadra, la superficie delimitada por la espira varía en el tiempo, Σ(t). Consideremos un instante arbitrario, t, en el cuál la barra se encuentra a una distancia x(t) del vértice O, y calculemos el flujo del campo magnético uniforme  a través de la superficie Σ(t), en el sentido positivo del eje OZ. Aunque el campo es uniforme y, por tanto, de módulo constante, este flujo magnético es variable en el tiempo al serlo la área
a través de la superficie Σ(t), en el sentido positivo del eje OZ. Aunque el campo es uniforme y, por tanto, de módulo constante, este flujo magnético es variable en el tiempo al serlo la área 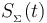 de la superficie delimitada por la espira:
de la superficie delimitada por la espira:
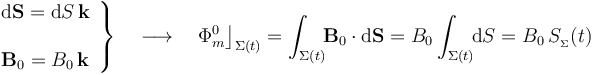
El valor de dicho área depende de la distancia x(t) de la barra al punto O: en todo instante, la espira  tiene la forma de un triángulo isósceles, cuyas altura y base miden x(t) y 2x(t), respectivamente, ya que el ángulo en el vértice O es π / 4. Por tanto, el flujo magnético instantáneo del campo
tiene la forma de un triángulo isósceles, cuyas altura y base miden x(t) y 2x(t), respectivamente, ya que el ángulo en el vértice O es π / 4. Por tanto, el flujo magnético instantáneo del campo  a través de la espira
a través de la espira  (medido en el sentido positivo del eje OZ), es:
(medido en el sentido positivo del eje OZ), es:
![\Phi_m^0\big\rfloor_{\Sigma(t)}=B_0\!\ \frac{1}2 x(t)\!\ \big[2x(t)\big]=B_0\!\ x^2(t)=\Phi_0(t)](/wiki/images/math/a/c/6/ac63b9a4a85b10ddcb184b67775a293b.png)
En virtud de la ley de Faraday, este flujo variable determinará la existencia de una fuerza electromotriz inducida  en la espira
en la espira  . Como veremos con más detalle en el siguiente apartado, la espira constituye un circuito cerrado sin generadores y con resistencia eléctrica
. Como veremos con más detalle en el siguiente apartado, la espira constituye un circuito cerrado sin generadores y con resistencia eléctrica 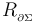 , por lo que se inducirá una corriente eléctrica de intensidad:
, por lo que se inducirá una corriente eléctrica de intensidad:
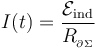
La ley de Biot y Savart establece que dicha corriente producirá un campo magnético “inducido” 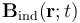 , que también contribuiría al flujo total de campo magnético a través de la superficie Σ delimitada por la espira:
, que también contribuiría al flujo total de campo magnético a través de la superficie Σ delimitada por la espira:
![\Phi_m\big\rfloor_{\Sigma(t)}=\int_{{}_{\Sigma(t)}}\!\! \left[\mathbf{B}_0+\mathbf{B}_\mathrm{ind}\right]\cdot\mathrm{d}\mathbf{S}=\Phi_0(t)+L(t)\!\ I(t)](/wiki/images/math/f/5/6/f563ca3773333f79c59ef26793cf72fa.png)
En la anterior expresión, el término correspondiente al flujo de la componente de campo inducido se ha expresado como el producto de la intensidad de corriente en la espira por la autoinducción L(t) de la espira, que sería función del tiempo al tener una geometría variable. De todas formas, en el enunciado se indica explícitamente que la autoinducción de la espira va a ser despreciable, lo cual supone admitir de forma ímplicita que la intensidad del campo magnético inducido tiene un valor poco significativo frente a la del campo uniforme:

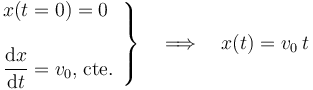
Por otra parte, la barra realiza un movimiento rectilíneo uniforme con celeridad constante v0, y de manera que en el instante inicial (t = 0), el centro de la bara se halla en el vértice O; por tanto, la expresión horaria para el flujo magnético a través de la espira será:


2.1.2 F.e.m. inducida
En consecuencia, la fuerza electromotriz inducida en la espira  debido a la variación del flujo a través de la superficie variable delimitada por aquélla, Σ(t), es:
debido a la variación del flujo a través de la superficie variable delimitada por aquélla, Σ(t), es:
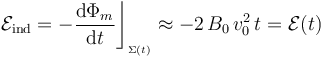
2.2 Corriente inducida
2.2.1 Intensidad de la corriente inducida en la espira
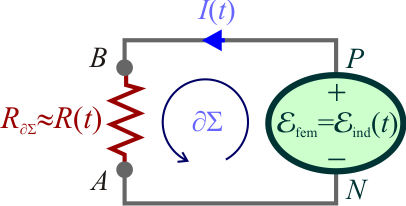
La espira constituye un circuito cerrado en el cual se verificará que la suma de todas las fuerzas electromotrices es igual al producto de la intensidad de la corriente por la resistencia eléctrica de la espira:
constituye un circuito cerrado en el cual se verificará que la suma de todas las fuerzas electromotrices es igual al producto de la intensidad de la corriente por la resistencia eléctrica de la espira:
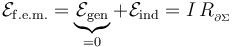
Recuérdese que al calcular el flujo en sentido positivo del eje OZ, la intensidad de corriente en la espira se ha de medir considerando que dicha corriente recorre la espira en sentido antihorario, visto desde el semiespacio correspondiente a los valores positivos de z.
En la espira no hay generadores, por tanto la única fuente de fuerza electromotriz es la inducida por el flujo magnético variable. En cuanto a la resistencia eléctrica, en el enunciado se indica que los conductores filiformes que forman la escuedra tienen resistencia eléctrica despreciable frente a la de la barra móvil de aluminio que cierra el circuito. Tampoco se hace mención a la resistencia de contacto entrela escuedra y dicha barra y, por lo que consideraremos que la resistencia eléctrica de la espira se reduce a la de la barra. No obstante, hay que tener cuidadado con esto pues, como se recordará, el concepto se resistencia eléctrica de un medio óhmico se define para el tubo de corriente que se forma en dicho medio. En el caso que nos ocupa, dicho tubo no se extiende a toda la barra, sino sólo al segmento de corriente comprendido entre los puntos de contacto B y A, y cuya longitud en un instante arbitrario es 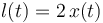 . Si se tiene en cuenta que la barra es rectilínea, podemos aplicar la expresión de la resistencia eléctrica de un conductor filiforme:
. Si se tiene en cuenta que la barra es rectilínea, podemos aplicar la expresión de la resistencia eléctrica de un conductor filiforme:


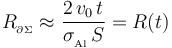
donde S es la sección de la barra móvil. Obsérvese que la resistencia eléctrica del segmento de conductor  (y por tanto la del circuito) varía con el tiempo cuando la barra se mueve.
(y por tanto la del circuito) varía con el tiempo cuando la barra se mueve.
A partir de la ecuación del circuito que inicia este apartado, se obtiene la expresión para la intensidad de la corriente inducida que recorre la espira  :
:
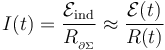


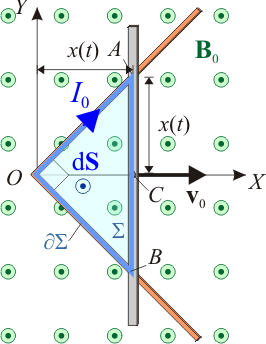
s decir, la corriente eléctrica inducida tiene intensidad constante de valor I0. El signo negativo indica que dicha corriente recorre la espira en sentido horario; es decir, en sentido opuesto al propuesto. Obviamente, este es un resultado coherente con la ley de Lenz: cuando la barra se desplaza en el sentido positivo del eje OX aumenta el flujo magnético del campo  (al medir aquél en el sentido positivo del eje OZ); segúna dicha ley, la corriente inducida debe recorrer la espira en sentido horario para producir así un campo magnético inducido que, dirigido en el sentido negativo del eje OZ, se oponga al aumento del flujo magnético.
(al medir aquél en el sentido positivo del eje OZ); segúna dicha ley, la corriente inducida debe recorrer la espira en sentido horario para producir así un campo magnético inducido que, dirigido en el sentido negativo del eje OZ, se oponga al aumento del flujo magnético.
2.2.2 Potencia y energía disipada por efecto Joule
Según la ley de Joule, la potencia disipada por efecto Joule en el segmento de la barra recorrida por la corriente es...
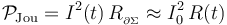


Es decir, la potencia instantánea disipada en forma de calor es proporcional al tiempo transcurrido desde que se incia el movimiento.
La energía disipada en el proceso completo es igual a la integral de la potencia desde el instante inicial hasta el momento tfin en que la barra móvil pierde contacto con la escuadra conductora. Si la longitud de la barra tiene un valor a, dicho instante final se produce cuando:

Por tanto, la energía disipada en forma de calor, por efecto Joule, es:


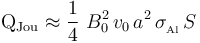
2.3 Fuerza magnética sobre la barra
El campo magnético ejerce una fuerza sobre la corriente eléctrica que se establece en la espira. En particular, la fuerza sobre la barra móvil (realmente sobre el segmento de corriente que se establece entre los puntos B y A responde a la expresión general: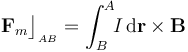
Nótese que en esta expresión mantenemos el sentido antohorario para el elemento de corriente. Además, la fuerza es ejercida por el campo magnético total resultante de la superposición del campo uniforme aplicado  con el creado por la corriente inducida. Sin embargo, como vimos en el primer apartado se puede considerar que el campo magnético inducido es despreciable frente al campo aplicado (autoinducción despreciable). Y como se trata de un campo uniforme y la intesidad de corriente es la misma en todos los puntos de la espira, se obtiene:
con el creado por la corriente inducida. Sin embargo, como vimos en el primer apartado se puede considerar que el campo magnético inducido es despreciable frente al campo aplicado (autoinducción despreciable). Y como se trata de un campo uniforme y la intesidad de corriente es la misma en todos los puntos de la espira, se obtiene:
![\mathbf{F}_m\big\rfloor_{{}_{AB}}\approx I(t)\bigg[\int_B^A\!\! \mathrm{d}\mathbf{r}\bigg]\times\mathbf{B}_0=-I_0\!\ \overrightarrow{BA}\times\mathbf{B}_0\quad\Longrightarrow](/wiki/images/math/1/b/3/1b366fdcbad00a900cef4ecd0535b190.png)


![\quad\mathbf{F}_m\big\rfloor_{{}_{AB}}\approx -I_0\!\ \big[2\!\ x(t)\!\ \mathbf{j}\big]\times\big(B_0\!\ \mathbf{k}\big)=-2I_0\!\ B_0\!\ x (t)\!\ \mathbf{i}](/wiki/images/math/e/f/c/efc6c42ec2d3294c6f3a04bb76e35cb4.png)
Es decir, la fuerza magnética que actúa sobre la barra móvil como consecuencia de la existencia de la corriente inducida, se opone al desplazamiento de aquélla. Es decir, se trata de otro aspecto del fenómeno en que se pone de manifiesto la ley de Lenz.