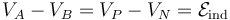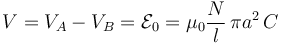Tensión inducida en espira, F2 GIA (Jun, 2013)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Campo magnético y flujo a través de la espira
- 2.2 Fuerza electromotriz inducida y tensión en el gap

1 Enunciado

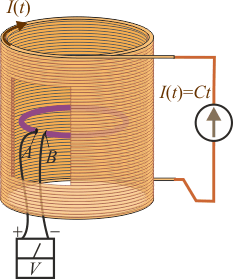
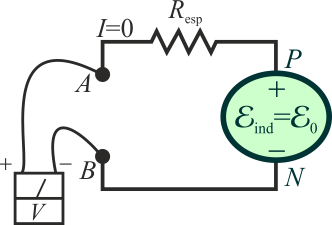
Un solenoide recto de forma cilíndrica y longitud

l

, mucho mayor que su radio, está formado por

N

espiras distribuidas de forma compacta que son recorridas en sentido horario por una corriente eléctrica que crece linealmente según la ley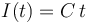 $I(t)=C\!\ t$ (

C

, constante). En un plano paralelo a las espiras del solenoide y en el interior de éste, se encuentra una pequeña espira circular de radio

a

, menor que el del solenoide. Si a la espira le falta un pequeño trozo, de manera que constituye un circuito abierto, ¿cómo es la tensión

V = V A - V B

que mediría un voltímetro conectado a sus extremos, tal como se indica en la figura?

2 Solución

2.1 Campo magnético y flujo a través de la espira

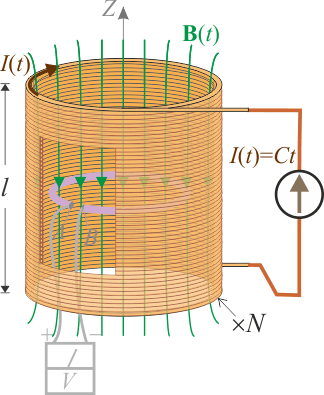
Como la longitud del solenoide cilíndrico es mucho mayor que su radio, podemos considerar que la corriente eléctrica que lo recorre sólo produce un campo apreciable en el interior de la bobina. Además, puede considerarse con buen grado de aproximación que, salvo en las proximidades de los extremos, dicho campo es uniforme y paralelo al eje de la bobina.

Tomemos a éste como eje $O Z$ de un sistema de referencia cartesiano, de manera que las espiras del solenoide se encuentren en planos paralelos al $O X Y$ y con la corriente eléctrica recorriéndolas en sentido horario. En cualquier punto del interior de la bobina, suficientemente alejado de sus extremos, el campo magnético será de la forma:

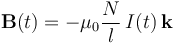
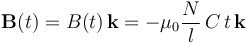
$\mathbf{B}(t)=-\mu_0\frac{N}{l}\!\ I(t)\!\ \mathbf{k}$ $\quad$ $\Rightarrow$ $\quad$ $\mathbf{B}(t)=B(t)\!\ \mathbf{k}=-\mu_0\frac{N}{l}\!\ C\!\ t\!\ \mathbf{k}$

Por tanto, ésta es la expresión del campo magnético 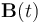$\mathbf{B}(t)$ , uniforme y variable en el tiempo, que existe en el entorno de la espira abierta localizada en el interior del solenoide.

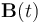Consideremos la circunferencia $\partial\Sigma$ coincidente con aquélla y con el gap o discontinuidad que hay entre los extremos $A$ y $B$ . Como dicho salto es pequeño, el flujo magnético a través de la espira es igual al flujo del vector $\mathbf{B}(t)$ en cualquier superficie que se apoye en la circunferencia $\partial\Sigma$ . Y puesto que el campo es perpendicular al plano que contiene a la espira, tomaremos como superficie $Σ$ el círculo de radio $a$ definido por la circunferencia $\partial\Sigma$ . Se obtendrá, por tanto:

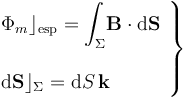
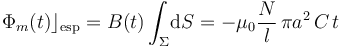
$\left.\begin{array}{l}\displaystyle \Phi_m\rfloor_\mathrm{esp}=\int_\Sigma\!\mathbf{B}\cdot\mathrm{d}\mathbf{S}\\ \\ \displaystyle\mathrm{d}\mathbf{S}\rfloor_\Sigma=\mathrm{d}S\!\ \mathbf{k}\end{array}\right\}$ $\quad$ $\Rightarrow$ $\quad$ $\Phi_m(t)\rfloor_\mathrm{esp}=B(t)\int_\Sigma\!\mathrm{d}S=-\mu_0\frac{N}{l}\!\ \pi a^2\!\ C\!\ t$

que, como puede comprobarse, se trata de un flujo magnético que crece linealmente en el tiempo.

2.2 Fuerza electromotriz inducida y tensión en el gap

En virtud de la ley de inducción, una variación temporal del flujo magnético a través de la espira da lugar a la aparición de una fuerza electromotriz inducida,

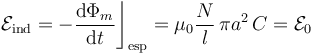
$\mathcal{E}_\mathrm{ind}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}\bigg\rfloor_\mathrm{esp}=\mu_0\frac{N}{l}\!\ \pi a^2\!\ C=\mathcal{E}_0$

cuyo valor constante 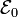$\mathcal{E}_0$ depende de la característica $C$ de la fuente de intensidad que alimenta a la bobina, y de los parámetros geométricos del sistema: $N$ , $l$ y $a$ . Si la espira constituyese un circuito cerrado, dicha fuerza electromotriz induciría una corriente eléctrica. Obsérvese que, en virtud de la ley de Lenz, dicha corriente recorrería la espira en sentido antihorario, ya que la elección del elemento de superficie 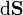$\mathrm{d}\mathbf{S}$ en sentido opuesto al campo magnético, da lugar a un flujo negativo magnético cuyo valor absoluto crece en el tiempo. Sin embargo, al presentar la espira un corte o gap entre los puntos $A$ y $B$ , la intensidad de corriente es nula, induciéndose una tensión $V A - V B$ entre dichos puntos.

Para deteminar la relación de ésta con la fuerza electromotriz inducida, construimos un modelo circuital para la espira abierta: consiste éste en un circuito abierto formado por una resistencia

R esp

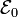en serie con un generador ideal. Aquélla modela la resistencia eléctrica del anillo conductor, mientras que la fuerza eléctromotriz del generador será igual a la $\mathcal{E}_0$ inducida por la variación del flujo magnético a través de la espira, ya que la espira no está conectada a fuente o dispositivo real alguno.

Obsérvese que si entre los extremos $A$ y $B$ de la espira se colocase un medio óhmico que permitiese el paso de corriente eléctrica, el sentido de ésta sería del extremo $A$ hacia el $B$ . En consecuencia, el circuito debe construirse de manera que los polos $P$ y $N$ del dispositivo que modela a la fuerza electromotriz estén conectados, respectivamente, a los extremos $A$ y $B$ de la espira. Como en la resistencia no se produce caída de tensión alguna, ya que la intensidad de corriente es nula, se tendrá que la señal de tensión entre los extremos de la espira coincide con la fuerza electromotriz inducida por la variación del flujo magnético a través de aquélla. Por tanto, la señal de tensión $V$ medida por el voltímetro conectado entre dichos extremos, es una diferencia de potencial (constante en el tiempo) positiva de valor 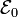$\mathcal{E}_0$ :

$V_A-V_B=V_P-V_N=\mathcal{E}_\mathrm{ind}$ $\Rightarrow$ $V=V_A-V_B=\mathcal{E}_0=\mu_0\frac{N}{l}\!\ \pi a^2\!\ C$

Tensión inducida en espira, F2 GIA (Jun, 2013)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo magnético y flujo a través de la espira

2.2 Fuerza electromotriz inducida y tensión en el gap

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES