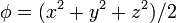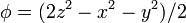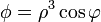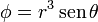Entrar Página Discusión Historial Go to the site toolbox

Cálculo de laplacianos

De Laplace

(Diferencias entre revisiones)
(→Primer campo)
(→Cuarto campo)
 
(8 ediciones intermedias no se muestran.)
Línea 12: Línea 12:
==Solución==
==Solución==
===Primer campo===
===Primer campo===
-
El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de [[cálculo de gradientes]] que su
+
El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de [[cálculo de gradientes]] que su gradiente vale
-
gradiente vale
+
<center><math>\nabla\phi = x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z} = \mathbf{r}</math></center>
<center><math>\nabla\phi = x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z} = \mathbf{r}</math></center>
Línea 22: Línea 21:
===Segundo campo===
===Segundo campo===
 +
Para el segundo campo, de nuevo calculamos su gradiente en [[cálculo de gradientes|un problema]] y la divergencia de éste en [[cálculo de divergencias y rotacionales|otro]], donde se ve que
 +
 +
<center>
 +
<math>\nabla^2\phi = \nabla{\cdot}(\nabla\phi) =
 +
\nabla{\cdot}\left(-x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\right)= 0</math></center>
 +
===Tercer campo===
===Tercer campo===
 +
Para el tercer campo, ya tenemos su expresión en cilíndricas. Calculamos el laplaciano en estas coordenadas
 +
 +
<center><math>\nabla^2\phi = \frac{1}{\rho}\frac{\partial\ }{\partial \rho}\left(\rho\frac{\partial \phi}{\partial \rho}\right)+
 +
\frac{1}{\rho^2}\frac{\partial^2 \phi}{\partial \varphi^2}+\frac{\partial^2 \phi}{\partial z^2} =
 +
9\rho\cos\varphi - \rho\cos\varphi = 8\rho\cos\varphi</math></center>
 +
 +
En cartesianas este campo se expresa
 +
 +
<center><math>\phi = (x^2+y^2)x = x^3 + y^2x\,</math></center>
 +
 +
y su laplaciano vale
 +
 +
<center><math>\nabla^2\phi = 6x + 2x = 8x</math></center>
 +
 +
En esféricas, la expresión del campo es
 +
 +
<center><math>\phi = r^3\mathrm{sen}^3\theta\cos\varphi</math></center>
 +
 +
y la del laplaciano, separando previamente los sumandos,
 +
 +
<center><math>\frac{1}{r^2}\frac{\partial \ }{\partial r}\left(r^2\frac{\partial \phi}{\partial r}\right) =
 +
12r\,\mathrm{sen}^3\theta\cos\varphi</math></center>
 +
 +
<center><math>\frac{1}{r^2\mathrm{sen}\,\theta}\frac{\partial \ }{\partial \theta}\left(\mathrm{sen}\,\theta\frac{\partial \phi}{\partial \theta}\right) =
 +
r\left(9\,\mathrm{sen}\,\theta\cos^2\theta-3\,\mathrm{sen}^3\theta\right)\cos\varphi
 +
= r\left(9\,\mathrm{sen}\,\theta-12\,\mathrm{sen}^3\theta\right)\cos\varphi
 +
</math></center>
 +
 +
<center><math>\frac{1}{r^2\mathrm{sen}^2\theta}\frac{\partial^2 \phi}{\partial \varphi^2} = -r\,\mathrm{sen}\,\theta\cos\varphi</math></center>
 +
 +
<center><math>\nabla^2\phi = 8r\,\mathrm{sen}\,\theta\cos\varphi</math></center>
 +
 +
Los tres resultados son naturalmente coincidentes.
 +
===Cuarto campo===
===Cuarto campo===
 +
En el último caso tenemos un campo expresado en esféricas
 +
 +
<center><math>\phi = r^3\mathrm{sen}\,\theta</math></center>
 +
 +
con laplaciano
 +
 +
<center><math>\nabla^2\phi = 12r\,\mathrm{sen}\,\theta + \frac{r}{\mathrm{sen}\,\theta}-2r\,\mathrm{sen}\,\theta = 10r\,\mathrm{sen}\,\theta + r\,\mathrm{cosec}\,\theta</math></center>
 +
\]
 +
Expresando este campo en cilíndricas
 +
 +
<center><math>\phi = \left(\rho^2+z^2\right)\rho = \rho^3 + z^2\rho</math></center>
 +
 +
resulta el laplaciano
 +
 +
<center><math>\nabla^2\phi = \frac{11\rho^2+z^2}{\rho}</math></center>
 +
 +
En cartesianas el campo se escribe
 +
 +
<center><math>\phi = (x^2+y^2+z^2)\sqrt{x^2+y^2}</math></center>
 +
 +
y su laplaciano como
 +
 +
<center><math>\nabla^2\phi = \frac{11x^2+11y^2+z^2}{\sqrt{x^2+y^2}}</math></center>
 +
 +
aunque los laboriosos cálculos que requiere aconsejan emplear coordenadas cilíndricas o esféricas.
[[Categoría:Problemas de fundamentos matemáticos]]
[[Categoría:Problemas de fundamentos matemáticos]]

última version al 08:37 25 sep 2008

Contenido

1 Enunciado

Calcule el laplaciano de los campos escalares

  1. \phi = (x^2+y^2+z^2)/2\,
  2. \phi = (2z^2-x^2-y^2)/2\,
  3. \phi = \rho^3\cos\varphi
  4. \phi = r^3\,\mathrm{sen}\,\theta

empleando coordenadas cartesianas, cilíndricas y esféricas.

2 Solución

2.1 Primer campo

El laplaciano se define como la divergencia del gradiente. Para el campo (1) se ve en el problema de cálculo de gradientes que su gradiente vale

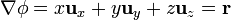
\nabla\phi = x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z} = \mathbf{r}

Hallar el laplaciano de \phi\, equivale a calcular la divergencia del vector de posición. Pero este cálculo ya se hace en el problema de cálculo de divergencias y rotacionales. Allí se ve que, independientemente del sistema empleado para calcularla

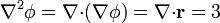
\nabla^2\phi = \nabla{\cdot}(\nabla\phi) = \nabla{\cdot}\mathbf{r} = 3

2.2 Segundo campo

Para el segundo campo, de nuevo calculamos su gradiente en un problema y la divergencia de éste en otro, donde se ve que

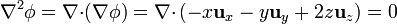
\nabla^2\phi = \nabla{\cdot}(\nabla\phi) = \nabla{\cdot}\left(-x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\right)= 0

2.3 Tercer campo

Para el tercer campo, ya tenemos su expresión en cilíndricas. Calculamos el laplaciano en estas coordenadas

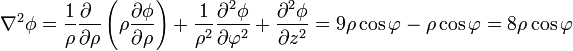
\nabla^2\phi = \frac{1}{\rho}\frac{\partial\ }{\partial \rho}\left(\rho\frac{\partial \phi}{\partial \rho}\right)+ \frac{1}{\rho^2}\frac{\partial^2 \phi}{\partial \varphi^2}+\frac{\partial^2 \phi}{\partial z^2} = 9\rho\cos\varphi - \rho\cos\varphi = 8\rho\cos\varphi

En cartesianas este campo se expresa

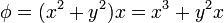
\phi = (x^2+y^2)x = x^3 + y^2x\,

y su laplaciano vale

\nabla^2\phi = 6x + 2x = 8x

En esféricas, la expresión del campo es

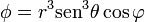
\phi = r^3\mathrm{sen}^3\theta\cos\varphi

y la del laplaciano, separando previamente los sumandos,

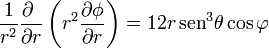
\frac{1}{r^2}\frac{\partial \ }{\partial r}\left(r^2\frac{\partial \phi}{\partial r}\right) = 12r\,\mathrm{sen}^3\theta\cos\varphi
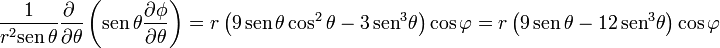
\frac{1}{r^2\mathrm{sen}\,\theta}\frac{\partial \ }{\partial \theta}\left(\mathrm{sen}\,\theta\frac{\partial \phi}{\partial \theta}\right) = r\left(9\,\mathrm{sen}\,\theta\cos^2\theta-3\,\mathrm{sen}^3\theta\right)\cos\varphi = r\left(9\,\mathrm{sen}\,\theta-12\,\mathrm{sen}^3\theta\right)\cos\varphi
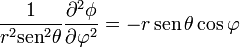
\frac{1}{r^2\mathrm{sen}^2\theta}\frac{\partial^2 \phi}{\partial \varphi^2} = -r\,\mathrm{sen}\,\theta\cos\varphi
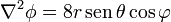
\nabla^2\phi = 8r\,\mathrm{sen}\,\theta\cos\varphi

Los tres resultados son naturalmente coincidentes.

2.4 Cuarto campo

En el último caso tenemos un campo expresado en esféricas

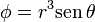
\phi = r^3\mathrm{sen}\,\theta

con laplaciano

\nabla^2\phi = 12r\,\mathrm{sen}\,\theta + \frac{r}{\mathrm{sen}\,\theta}-2r\,\mathrm{sen}\,\theta = 10r\,\mathrm{sen}\,\theta + r\,\mathrm{cosec}\,\theta

\] Expresando este campo en cilíndricas

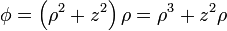
\phi = \left(\rho^2+z^2\right)\rho = \rho^3 + z^2\rho

resulta el laplaciano

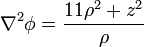
\nabla^2\phi = \frac{11\rho^2+z^2}{\rho}

En cartesianas el campo se escribe

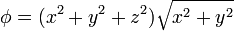
\phi = (x^2+y^2+z^2)\sqrt{x^2+y^2}

y su laplaciano como

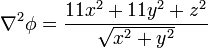
\nabla^2\phi = \frac{11x^2+11y^2+z^2}{\sqrt{x^2+y^2}}

aunque los laboriosos cálculos que requiere aconsejan emplear coordenadas cilíndricas o esféricas.

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_laplacianos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 08:37, 25 sep 2008. - Esta página ha sido visitada 33.339 veces. - Aviso legal - Acerca de Laplace