Problemas de electrostática en medios materiales (GIE)
De Laplace
(→Cuatro placas conductoras paralelas) |
(→Dos esferas conductoras dentro de otra) |
||
| (41 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | =Problemas de boletín= | ||
==[[Esfera conductora en equilibrio electrostático]]== | ==[[Esfera conductora en equilibrio electrostático]]== | ||
Se tiene una esfera metálica maciza de radio <math>a</math> y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total <math>Q</math> calcule: | Se tiene una esfera metálica maciza de radio <math>a</math> y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total <math>Q</math> calcule: | ||
| Línea 9: | Línea 10: | ||
Particularice los resultados anteriores para un radio <math>a = 10\,\mathrm{cm}</math> y una carga <math>Q= 36\,\mathrm{nC}</math>. | Particularice los resultados anteriores para un radio <math>a = 10\,\mathrm{cm}</math> y una carga <math>Q= 36\,\mathrm{nC}</math>. | ||
| - | Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 12\,\mathrm{V}</math>. | + | Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 1.8\,\mathrm{kV}</math>. |
| + | |||
| + | ==[[Dos esferas conductoras concéntricas]]== | ||
| + | Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como | ||
| + | la energía almacenada en el sistema, para los siguientes casos: | ||
| + | |||
| + | # La esfera almacena una carga de +4 nC y la corona está aislada y descargada. | ||
| + | # La esfera está aislada y descargada y la corona almacena +6 nC | ||
| + | # La esfera almacena una carga de +4 nC y la corona de +6 nC | ||
| + | # La esfera almacena una carga de −4 nC y la corona de +4 nC | ||
| + | # La esfera almacena una carga de −4 nC y la corona de +6 nC | ||
| + | # La esfera almacena una carga de +4 nC y la corona está a tierra | ||
| + | # La esfera está a tierra y la corona almacena una carga de +6 nC | ||
| + | # La esfera está a +2 kV y la corona está a tierra. | ||
| + | # La esfera está a tierra y la corona a +2 kV. | ||
| + | # La esfera y la corona están a +2 kV | ||
| + | # La esfera está a +2 kV y la corona está a −2 kV. | ||
| + | |||
| + | '''Sugerencia:''' Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente. | ||
| + | |||
| + | ==[[Conexión de dos esferas alejadas]]== | ||
| + | Se tiene un conductor formado por dos esferas de radios <math>a</math> y <math>b</math> (<math>a<b</math>), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga <math>Q_0</math>. | ||
| + | |||
| + | # ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada? | ||
| + | # ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie? | ||
| + | |||
| + | <center>[[Imagen:dosesferashilo-02.png]]</center> | ||
| + | |||
| + | ==[[Conexión de una fuente a un conductor]]== | ||
| + | Un determinado sistema está formado exclusivamente por un conductor de capacidad <math>C</math>. Inicialmente este conductor almacena una carga <math>Q_A</math>. | ||
| + | |||
| + | Una fuente de tensión continua <math>V_B</math> se conecta al conductor mediante un interruptor que se cierra bruscamente. | ||
| + | |||
| + | # ¿Cuánto cambia la carga almacenada en el conductor? | ||
| + | # ¿Cuánto cambia la energía electrostática del sistema? | ||
| + | # ¿Qué trabajo realiza la fuente en este proceso? ¿Cuánta energía se disipa? | ||
| + | # Supóngase ahora que la fuente es una de tensión regulable que se hace variar lentamente desde <math>V_A</math> (la correspondiente al estado inicial) a <math>V_B</math>. ¿Cómo quedan en ese caso las respuestas a los tres apartados anteriores? | ||
| + | |||
| + | ==[[Tres placas conductoras paralelas]]== | ||
| + | Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm y ésta de la tercera 0.8 mm. Halle: | ||
| + | |||
| + | # La carga almacenada en cada placa. | ||
| + | # El potencial al que se encuentra cada una. | ||
| + | # El campo eléctrico entre las placas. | ||
| + | # La energía almacenada en el sistema. | ||
| + | |||
| + | para los siguientes casos: | ||
| + | |||
| + | * La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra. | ||
| + | * La placa central está a 24 V y las otras dos a tierra. | ||
| + | * La primera está a −24 V, la central a +24 V y la tercera a tierra. | ||
| + | * La placa central almacena una carga de 4 nC y las dos placas exteriores están conectadas entre sí. | ||
| + | |||
| + | ==[[Sistema de cuatro condensadores]]== | ||
| + | [[Archivo:cuatro-condensadores.png|right]] | ||
| + | |||
| + | El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: <math>C_1=30\,\mathrm{nF}</math>, <math>C_2=60\,\mathrm{nF}</math>, <math>C_3=120\,\mathrm{nF}</math> y <math>C_4=40\,\mathrm{nF}</math>. La diferencia de potencial entre A y B es de <math>12\,\mathrm{V}</math>. ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema. | ||
| + | |||
| + | Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada? | ||
| + | |||
| + | ==[[Condensador que se rellena de dieléctrico]]== | ||
| + | El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío. | ||
| + | |||
| + | Entre las placas se establece una diferencia de potencial de 20 V | ||
| + | |||
| + | # ¿Cuánto vale la energía almacenada en el sistema? | ||
| + | # Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (<math>\varepsilon_r = 3.3</math>) de 3 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia? | ||
| + | # Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión? | ||
| + | |||
| + | ==[[Condensador que se gira 90°]]== | ||
| + | Se construye un recipiente cilíndrico, con bases perfectamente conductoras de sección <math>S</math>, separadas una distancia <math>a</math>, y paredes perfectamente dieléctricas, de espesor despreciable. El interior se llena hasta la mitad con un líquido dieléctrico y permitividad <math>\varepsilon</math>. El resto se deja vacío. | ||
| + | |||
| + | El recipiente se coloca en un principio con las bases dispuestas horizontalmente. En esta posición, se carga hasta que la diferencia de potencial entre las placas es <math>V_0</math>. Acto seguido se abre el circuito y, sin descargar las placas, el recipiente es girado <math>90^\circ</math> alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada? | ||
| + | |||
| + | Desprecie los efectos de borde y la influencia de las paredes. | ||
| + | |||
| + | <center>[[Imagen:recipientev.gif]]{{qquad}}{{qquad}}[[Imagen:recipienteh.gif]]</center> | ||
| + | |||
| + | ==[[Cuatro conductores paralelos]]== | ||
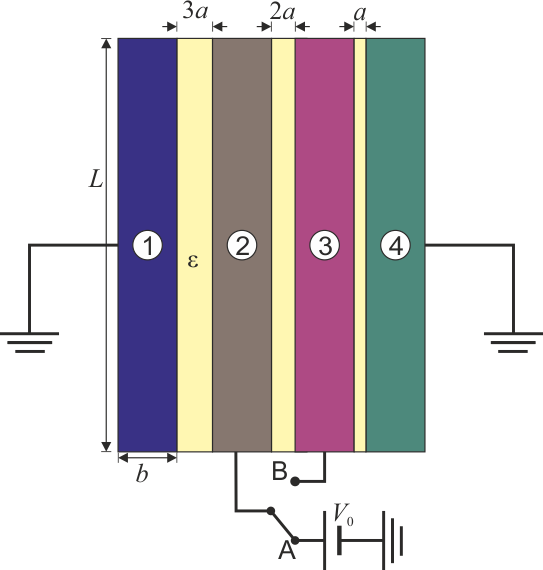
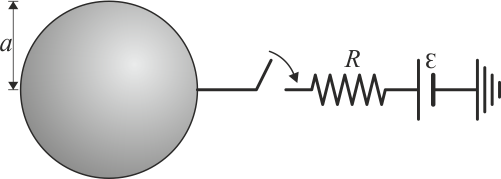
| + | Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado <math>L=20\,\mathrm{cm}</math> de lado y grosor <math>b=1\,\mathrm{cm}</math>. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio <math>3a</math>; entre el 2º y el 3º hay <math>2a</math> y entre el 3º y el 4º hay <math>a</math>, siendo <math>a=1\,\mathrm{mm}</math>. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad <math>\varepsilon=30\,\mathrm{pF}/\mathrm{m}</math>. | ||
| + | |||
| + | El conductor 1 y el 4 se encuentran permanentemente a tierra. | ||
| + | |||
| + | <center>[[Archivo:fuente-cuatro-bloques.png]]</center> | ||
| + | |||
| + | Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial <math>V_0=125\,\mathrm{V}</math>$, mientras que el 3 está aislado y descargado. | ||
| + | |||
| + | # Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores. | ||
| + | # Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras | ||
| + | # Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies? | ||
| + | # Halle la energía almacenada en el sistema antes y después de mover el interruptor. | ||
| + | ¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía? | ||
| + | |||
| + | =Problemas adicionales= | ||
| + | ==[[Esfera que se conecta a una fuente de tensión]]== | ||
| + | Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga <math>Q_1=10\,\mathrm{nC}</math>. Alrededor de la esfera no hay más conductores ni cargas. | ||
| + | |||
| + | <center>[[Archivo:esfera-fuente.png]]</center> | ||
| + | |||
| + | # Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema. | ||
| + | # Suponga que ahora se conecta a la esfera una fuente de tensión de 0.3 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera? | ||
| + | # Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema? | ||
| + | # ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia? | ||
| + | # Determine la ecuación diferencial que gobierna el potencial <math>V(t)</math> de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de <math>V(t)</math> frente al tiempo. | ||
| + | |||
| + | '''Dato:''' <math>1/(4\pi\varepsilon_0) = 9\times 10^9\,\mathrm{m}/\mathrm{F}</math> | ||
==[[Carga en el interior de una corona esférica]]== | ==[[Carga en el interior de una corona esférica]]== | ||
| Línea 24: | Línea 130: | ||
* La corona está aislada y descargada. | * La corona está aislada y descargada. | ||
* La corona está conecta a una fuente de tensión que fija un voltaje <math>V_0 = -12\,\mathrm{V}</math>. | * La corona está conecta a una fuente de tensión que fija un voltaje <math>V_0 = -12\,\mathrm{V}</math>. | ||
| - | * | + | * La corona está aislada y almacena una carga <math>Q_0=-36\,\mathrm{nC}</math>. |
| + | |||
| + | ==[[Esfera rodeada de corona esférica]]== | ||
| + | Se tiene una esfera conductora de radio <math>a</math> que almacena una carga <math>Q_0</math>. Rodeándola se halla una corona esférica también conductora de radio interior <math>2a</math> y exterior <math>4a</math>. Esta corona se halla inicialmente aislada y descargada. | ||
| + | |||
| + | # Calcule el campo eléctrico en todos los puntos del espacio. Puede suponerse que las distribuciones de carga son todas uniformes. | ||
| + | # Determine el potencial al que se encuentra la esfera interior. | ||
| + | # Calcule la energía electrostática almacenada en el sistema. | ||
| + | # Suponga que se conecta la corteza exterior a tierra. Una vez que se vuelve al equilibrio electrostático, ¿cómo cambia el potencial de la esfera interior y la energía almacenada? ¿A qué se debe la diferencia de energía? | ||
==[[Condensador plano de placas circulares]]== | ==[[Condensador plano de placas circulares]]== | ||
Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V. | Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V. | ||
| - | Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa <math>\varepsilon_r=2</math> | + | Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa <math>\varepsilon_r=2</math>. ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas? |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==[[Cuatro placas conductoras paralelas]]== | ==[[Cuatro placas conductoras paralelas]]== | ||
| Línea 55: | Línea 154: | ||
¿Cómo cambian los resultados se conectan las placas centrales sin desconectar previamente la fuente de tensión? ¿Qué trabajo realiza la fuente en este caso? | ¿Cómo cambian los resultados se conectan las placas centrales sin desconectar previamente la fuente de tensión? ¿Qué trabajo realiza la fuente en este caso? | ||
| - | ==[[ | + | ==[[Condensador que se rellena parcialmente de dieléctrico]]== |
| - | + | El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío. | |
| - | + | Entre las placas se establece una diferencia de potencial de 20 V | |
| - | Suponga que, | + | # ¿Cuánto vale la energía almacenada en el sistema? |
| + | # Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (<math>\varepsilon_r = 3.3</math>) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia? | ||
| + | # Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión? | ||
| - | ==[[ | + | ==[[Capacidad de la tierra y la ionosfera]]== |
| - | + | La tierra y la ionosfera pueden considerarse que forman un condensador esférico. Si el radio de la tierra es de aproximadamente 6400 km y la ionosfera está a 100 km de altura, ¿cuánto vale la capacidad de este condensador? | |
| - | + | ==[[Sistema con tres conductores esféricos]]== | |
| + | En una esfera metálica de radio 36 mm se han hecho dos cavidades, también esféricas, de radio 18 mm. Concéntricas con cada una de estos huecos se hallan sendas esferas metálicas de radio 9 mm. No hay más conductores en el sistema. Suponga que la esfera exterior se encuentra aislada y descargada; una de las esferas interiores se encuentra a un potencial 8 kV y la otra se encuentra a tierra. | ||
| - | + | <center>[[Archivo:esfera-dos-huecos.png]]</center> | |
| - | ==[[ | + | # ¿Cuál es la carga en cada conductor? ¿Y el potencial? |
| - | La | + | # Halle la energía almacenada en el sistema. |
| + | # Si tomamos como eje OX el que pasa por los tres centros y origen O el centro del sistema, calcule el módulo del campo eléctrico en las siguientes posiciones | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! x (mm) | ||
| + | ! <math>\left|\vec{E}|\right|</math> | ||
| + | |- | ||
| + | | −16 | ||
| + | | | ||
| + | |- | ||
| + | | −8 | ||
| + | | | ||
| + | |- | ||
| + | | +8 | ||
| + | | | ||
| + | |- | ||
| + | | +16 | ||
| + | | | ||
| + | |- | ||
| + | | +24 | ||
| + | | | ||
| + | |- | ||
| + | | +28 | ||
| + | | | ||
| + | |} | ||
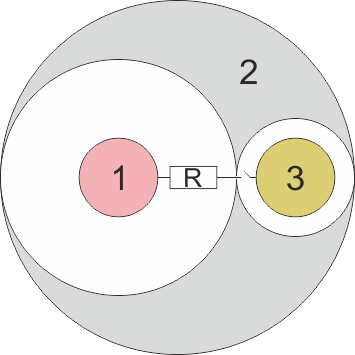
| + | ==[[Dos esferas conductoras dentro de otra]]== | ||
| + | Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36 mm y 18 mm. En el centro de cada hueco se encuentran sendas esferas metálicas de radio 12 mm, | ||
| + | siendo “1” la que está en el hueco grande y “3” la que está en el pequeño. Entre las esferas hay vacío y no hay más conductores ni cargas en el sistema. | ||
| + | |||
| + | Inicialmente la esfera “1” contiene una carga 120 nC mientras que los otros dos conductores están aislados y descargados. | ||
| + | |||
| + | # Halle el potencial de cada conductor, así como la energía almacenada en el sistema. | ||
| + | # Se conectan las dos esferas interiores mediante un hilo de resistencia 1 kΩ. Una vez que se ha vuelto a alcanzar el estado final, ¿cuáles son los nuevos potenciales de los conductores? | ||
| + | # ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia? | ||
| + | # Halle la potencia instantánea disipada en el cable justo tras la conexión. | ||
| + | |||
| + | Tómese | ||
| + | <center><math>\frac{1}{4\pi\varepsilon_0}\simeq 9\times 10^9\,\frac{\mathrm{m}}{\mathrm{F}}</math></center> | ||
| + | |||
| + | <center>[[Archivo:tres-esferas-conductoras.png]]</center> | ||
| + | |||
| + | ==[[Tres superficies conductoras concéntricas (GIE)|Tres superficies conductoras concéntricas]] | ||
| + | Se tiene un sistema formado por tres superficies conductoras esféricas concéntricas, de radios <math>2b</math>, <math>3b</math> y <math>6b</math>. Inicialmente la esfera interior almacena una carga <math>-Q_0</math>, la intermedia está aislada y descargada y la exterior almacena una carga <math>+Q_0</math>. | ||
| + | <center>[[Archivo:tres-esferas-interruptor.png|600px]]</center> | ||
| + | |||
| + | # Calcule el potencial al que se encuentra cada esfera. | ||
| + | # Halle el campo eléctrico en los puntos del eje OZ siguientes: <math>z=0</math>, <math>z=5b/2</math>, <math>z=4b</math> y <math>z=8b</math>, siendo el origen de coordenadas el centro de las esferas. | ||
| + | # Halle la energía almacenada en el sistema | ||
| + | |||
| + | En un momento dado se cierra el interruptor que conecta la esfera intermedia a tierra. Una vez que se alcanza de nuevo el equilibrio electrostático: | ||
| + | <ol start="4"> | ||
| + | <li>¿Cuáles son las nuevas cargas y potenciales de los tres conductores?</li> | ||
| + | <li>¿Cuánto vale ahora el campo eléctrico en los puntos del apartado 2?</li> | ||
| + | <li>¿Cuánto vale la energía almacenada en el sistema?</li> | ||
| + | <li>¿Cuánta energía se ha perdido en el proceso?</li> | ||
| + | </ol> | ||
| + | |||
| + | =[[Preguntas de test de electrostática en medios materiales|Preguntas de test]]= | ||
| + | ==Asociación de tres condensadores== | ||
| + | Dado el sistema de tres condensadores de la figura, | ||
| + | |||
| + | <center>[[Archivo:tres-condensadores.png|300px]]</center> | ||
| + | |||
| + | ¿cuánto vale la capacidad equivalente entre A y B? | ||
| + | |||
| + | :*'''A''' 2 nF. | ||
| + | :*'''B''' 9 nF. | ||
| + | :*'''C''' 4 nF. | ||
| + | :*'''D''' 18 nF. | ||
| + | |||
| + | ==Reparto de carga entre dos esferas== | ||
| + | Dos esferas metálicas de 30 cm y 10 cm de radio están muy alejadas. La primera tiene una carga de 10 nC y la segunda está descargada. Se conectan por un hilo metálico. ¿Cómo se reparte la carga entre la grande y la pequeña? | ||
| + | |||
| + | :*'''A''' 50% - 50% | ||
| + | :*'''B''' 90% - 10% | ||
| + | :*'''C''' 75% - 25% | ||
| + | :*'''D''' 100% - 0% | ||
| + | |||
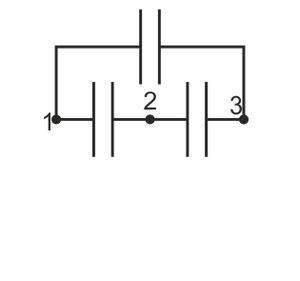
| + | ==Sistema de tres conductores== | ||
| + | Se tiene el sistema de conductores en equilibrio electrostático de la figura, en la que se han indicado algunas de las líneas de campo eléctrico | ||
| + | |||
| + | <center>[[Archivo:tres-conductores.png]]</center> | ||
| + | |||
| + | ¿Qué podemos decir de los potenciales de cada conductor (tomando como origen de potencial el infinito)? | ||
| + | |||
| + | :*'''A''' <math>V_1 > V_2 > 0 > V_3</math> | ||
| + | :*'''B''' Tal situación es imposible. | ||
| + | :*'''C''' <math>V_1 > 0 > V_2 > V_3</math> | ||
| + | :*'''D''' <math>V_1 > V_2 > V_3 > 0</math> | ||
| + | |||
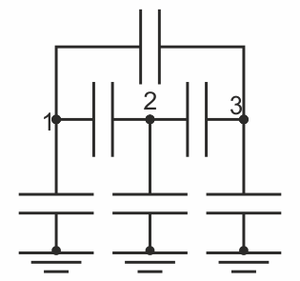
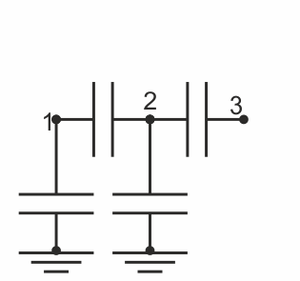
| + | ¿Cómo sería el sistema de condensadores que representa a este sistema de conductores? | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:circ-tres-cond-a.png|300px]] | ||
| + | | [[Archivo:circ-tres-cond-b.png|300px]] | ||
| + | |- | ||
| + | ! A | ||
| + | ! B | ||
| + | |- | ||
| + | | [[Archivo:circ-tres-cond-c.png|300px]] | ||
| + | | [[Archivo:circ-tres-cond-d.png|300px]] | ||
| + | |- | ||
| + | ! C | ||
| + | ! D | ||
| + | |} | ||
| + | |||
| + | ==Condensador con dieléctrico== | ||
| + | Se tiene un condensador plano formado por dos placas circulares de radio 10 cm separadas una distancia de 1 mm. Entre ellas hay una lámina de dieléctrico de permitividad <math>\varepsilon=2\varepsilon_0</math>. La lámina llena todo el espacio entre las placas. Se aplica entre las placas una diferencia de potencial de 100 V | ||
| + | |||
| + | ¿Cuánto vale la energía almacenada en el sistema? | ||
| + | |||
| + | :*'''A''' 2.78 μJ. | ||
| + | :*'''B''' 0.556 nJ. | ||
| + | :*'''C''' 1.39 μJ. | ||
| + | :*'''D''' 5.56 μJ. | ||
| + | |||
| + | Sin desconectar la fuente se retira la lámina de dieléctrico. En este proceso la energía almacenada… | ||
| + | |||
| + | :*'''A''' aumenta al cuádruple. | ||
| + | :*'''B''' aumenta al doble. | ||
| + | :*'''C''' se reduce a la mitad. | ||
| + | :*'''D''' se queda igual. | ||
| + | |||
| + | ==Condensador relleno de papel== | ||
| + | Se construye un condensador plano colocando horizontalmente un disco de radio 10 cm, sobre él una hoja de papel de 0.1 mm de espesor con permitividad <math>\varepsilon_r = 3.0</math> y sobre ésta se apoya otro disco metálico del mismo radio. | ||
| + | |||
| + | ¿Cuánto vale la capacidad del condensador resultante? | ||
| + | |||
| + | :*'''A''' 0.085 pF. | ||
| + | :*'''B''' 8.34 nF. | ||
| + | :*'''C''' 2.78 nF. | ||
| + | :*'''D''' 26.6 nF. | ||
| + | |||
| + | La placa superior se eleva una distancia de 0.1 mm, separándola del papel, ¿cuánto vale la nueva capacidad del condensador? | ||
| + | |||
| + | :*'''A''' 4.17 nF. | ||
| + | :*'''B''' 11.12 nF | ||
| + | :*'''C''' 2.09 nF. | ||
| + | :*'''D''' 16.7 nF | ||
| + | |||
| + | ==Carga frente a esfera== | ||
| + | Una esfera conductora se encuentra conectada a tierra. Frente a | ||
| + | ella se coloca una carga puntual positiva. ¿Como son el potencial y la carga de | ||
| + | la esfera? | ||
| + | |||
| + | :*'''A''' <math>V = 0</math> y <math>Q < 0</math> | ||
| + | :*'''B''' <math>V = 0</math> y <math>Q = 0</math> | ||
| + | :*'''C''' <math>V > 0</math> y <math>Q = 0</math> | ||
| + | :*'''D''' <math>V > 0</math> y <math>Q > 0</math> | ||
| + | |||
| + | ==Dieléctrico con dos capas== | ||
| + | Se tiene el condensador de la figura, formado por dos placas conductoras paralelas de sección <math>S</math> y distancia entre placas <math>a</math>. Entre ellas la mitad del espacio está ocupado por un dieléctrico ideal de permitividad relativa 1.5 y la otra mitad por uno de permitividad 3.0, siendo la frontera paralela a las placas. La capacidad del condensador en vacío en ausencia de los dieléctricos es <math>C_0</math>. | ||
| + | |||
| + | <center>[[Archivo:condensador-dos-capas-02.png]]</center> | ||
| + | |||
| + | ¿Cuánto vale la capacidad de este condensador? | ||
| + | |||
| + | :*'''A''' <math>C=4.5C_0</math> | ||
| + | :*'''B''' <math>C=2.25C_0</math> | ||
| + | :*'''C''' <math>C=0.5C_0</math> | ||
| + | :*'''D''' <math>C=2.0C_0</math> | ||
| + | |||
| + | Suponga que este condensador se conecta a una fuente de tensión <math>V_0</math>. Si <math>E_1</math> es el campo en el material de permitividad 1.5 y <math>E_2</math> en el de permitividad 3.0, ¿cómo se relacionan estos dos campos? | ||
| + | |||
| + | :*'''A''' Puede darse cualquiera de las otras tres posibilidades. | ||
| + | :*'''B''' <math>E_1 > E_2</math> | ||
| + | :*'''C''' <math>E_1 < E_2</math> | ||
| + | :*'''D''' <math>E_1 = E_2</math> | ||
| + | |||
| + | ==Dos conductores enfrentados== | ||
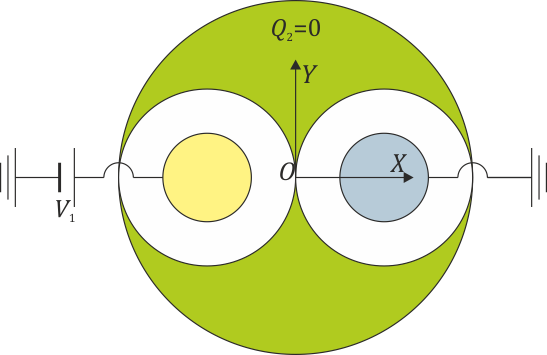
| + | Se colocan dos conductores uno frente al otro. El primero tiene <math>Q_1>0</math> y el segundo <math>Q_2=0</math>. No hay más cargas ni conductores en el sistema. ¿Qué podemos decir de sus potenciales? | ||
| + | |||
| + | :*'''A''' <math>V_1>0</math>, <math>V_2<0</math>. | ||
| + | :*'''B''' <math>V_1>0</math>, <math>V_2>0</math>. | ||
| + | :*'''C''' <math>V_1=0</math>, <math>V_2<0</math>. | ||
| + | :*'''D''' <math>V_1>0</math>, <math>V_2=0</math>. | ||
| + | |||
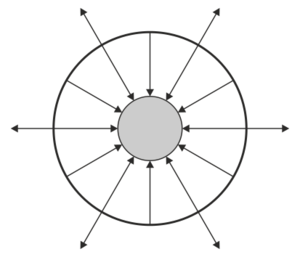
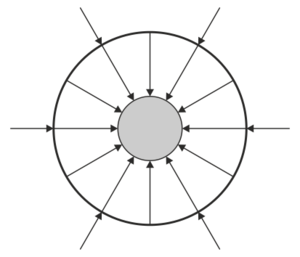
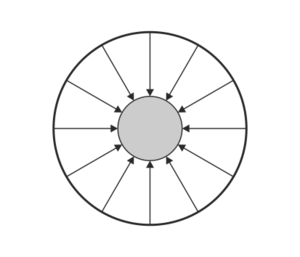
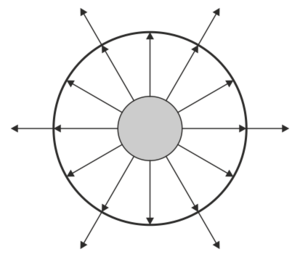
| + | ==Dos superficies esféricas== | ||
| + | Se tienen dos superficies conductoras esféricas concéntricas, de radios 1 cm y 3 cm, respectivamente. Inicialmente la interior (1) almacena una carga de | ||
| + | <math>-</math>40 nC y la exterior (2) una de +20 nC. | ||
| + | |||
| + | ¿Cuál de las siguientes figuras describe adecuadamente el campo eléctrico en el sistema? | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:dos-esferas-concentricas-a.png|300px]] | ||
| + | | [[Archivo:dos-esferas-concentricas-b.png|300px]] | ||
| + | |- | ||
| + | ! A | ||
| + | ! B | ||
| + | |- | ||
| + | | [[Archivo:dos-esferas-concentricas-c.png|300px]] | ||
| + | | [[Archivo:dos-esferas-concentricas-d.png|300px]] | ||
| + | |- | ||
| + | ! C | ||
| + | ! D | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Se conectan las dos esferas por un cable. Una vez que se alcanza el equilibrio electrostático, ¿cómo queda el reparto de cargas entre las dos? | ||
| + | |||
| + | :*'''A''' <math>Q_1=-2\,\mathrm{nC}</math>, <math>Q_2 = -18\,\mathrm{nC}</math> | ||
| + | :*'''B''' <math>Q_1=-5\,\mathrm{nC}</math>, <math>Q_2 = -15\,\mathrm{nC}</math> | ||
| + | :*'''C''' <math>Q_1=0\,\mathrm{nC}</math>, <math>Q_2 = -20\,\mathrm{nC}</math> | ||
| + | :*'''D''' <math>Q_1=-10\,\mathrm{nC}</math>, <math>Q_2 = -10\,\mathrm{nC}</math> | ||
| + | |||
| + | ==Tres placas circulares== | ||
| + | Tres placas conductoras circulares de radio 12 cm se encuentran situadas paralelamente con una distancia de 1 mm entre ellas. El espacio intermedio está vacío. La placa central se encuentra a un potencial de 100 V, mientras que las exteriores están puestas a tierra. | ||
| + | |||
| + | <center>[[Archivo:Tres-placas-paralelas.png]]</center> | ||
| + | |||
| + | La energía electrostática almacenada en el sistema vale… | ||
| + | |||
| + | :*'''A''' 4 μJ | ||
| + | :*'''B''' 8 μJ | ||
| + | :*'''C''' 2 μJ | ||
| + | :*'''D''' 1 μJ | ||
| + | |||
| + | ==Comparación de dos condensadores== | ||
| + | Se tienen dos condensadores planos de las mismas dimensiones (sección y espesor). El 1 está relleno de un dieléctrico con permitividad relativa 3.0 y el 2 de un dieléctrico con permitividad 1.5. En un momento dado, los dos están cargados con la misma carga <math>Q_0</math>. ¿En cuál de ellos es mayor el campo eléctrico interior? | ||
| + | |||
| + | :*'''A''' En el 2. | ||
| + | :*'''B''' Vale lo mismo en los dos. | ||
| + | :*'''C''' En el 1. | ||
| + | :*'''D''' No hay suficiente información para saberlo. | ||
[[Categoría:Problemas de electrostática en medios materiales (GIE)|0]] | [[Categoría:Problemas de electrostática en medios materiales (GIE)|0]] | ||
| + | [[Categoría:Electrostática en medios materiales (GIE)]] | ||
[[Categoría:Problemas de electricidad y magnetismo (GIE)]] | [[Categoría:Problemas de electricidad y magnetismo (GIE)]] | ||
última version al 21:43 8 may 2017
1 Problemas de boletín
1.1 Esfera conductora en equilibrio electrostático
Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:
- el potencial y el campo eléctrico en todos los puntos del espacio.
- el voltaje al que se encuentra
- la densidad superficial de carga.
- la energía electrostática que almacena.
Particularice los resultados anteriores para un radio  y una carga
y una carga 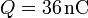 .
.
Suponga ahora que lo que se conoce inicialmente su voltaje V0, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje 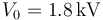 .
.
1.2 Dos esferas conductoras concéntricas
Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como la energía almacenada en el sistema, para los siguientes casos:
- La esfera almacena una carga de +4 nC y la corona está aislada y descargada.
- La esfera está aislada y descargada y la corona almacena +6 nC
- La esfera almacena una carga de +4 nC y la corona de +6 nC
- La esfera almacena una carga de −4 nC y la corona de +4 nC
- La esfera almacena una carga de −4 nC y la corona de +6 nC
- La esfera almacena una carga de +4 nC y la corona está a tierra
- La esfera está a tierra y la corona almacena una carga de +6 nC
- La esfera está a +2 kV y la corona está a tierra.
- La esfera está a tierra y la corona a +2 kV.
- La esfera y la corona están a +2 kV
- La esfera está a +2 kV y la corona está a −2 kV.
Sugerencia: Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente.
1.3 Conexión de dos esferas alejadas
Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q0.
- ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
- ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?

1.4 Conexión de una fuente a un conductor
Un determinado sistema está formado exclusivamente por un conductor de capacidad C. Inicialmente este conductor almacena una carga QA.
Una fuente de tensión continua VB se conecta al conductor mediante un interruptor que se cierra bruscamente.
- ¿Cuánto cambia la carga almacenada en el conductor?
- ¿Cuánto cambia la energía electrostática del sistema?
- ¿Qué trabajo realiza la fuente en este proceso? ¿Cuánta energía se disipa?
- Supóngase ahora que la fuente es una de tensión regulable que se hace variar lentamente desde VA (la correspondiente al estado inicial) a VB. ¿Cómo quedan en ese caso las respuestas a los tres apartados anteriores?
1.5 Tres placas conductoras paralelas
Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm y ésta de la tercera 0.8 mm. Halle:
- La carga almacenada en cada placa.
- El potencial al que se encuentra cada una.
- El campo eléctrico entre las placas.
- La energía almacenada en el sistema.
para los siguientes casos:
- La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra.
- La placa central está a 24 V y las otras dos a tierra.
- La primera está a −24 V, la central a +24 V y la tercera a tierra.
- La placa central almacena una carga de 4 nC y las dos placas exteriores están conectadas entre sí.
1.6 Sistema de cuatro condensadores
El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: 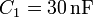 ,
, 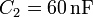 ,
, 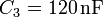 y
y 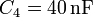 . La diferencia de potencial entre A y B es de
. La diferencia de potencial entre A y B es de 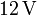 . ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
. ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?
1.7 Condensador que se rellena de dieléctrico
El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.
Entre las placas se establece una diferencia de potencial de 20 V
- ¿Cuánto vale la energía almacenada en el sistema?
- Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (
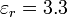 ) de 3 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
) de 3 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
- Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?
1.8 Condensador que se gira 90°
Se construye un recipiente cilíndrico, con bases perfectamente conductoras de sección S, separadas una distancia a, y paredes perfectamente dieléctricas, de espesor despreciable. El interior se llena hasta la mitad con un líquido dieléctrico y permitividad  . El resto se deja vacío.
. El resto se deja vacío.
El recipiente se coloca en un principio con las bases dispuestas horizontalmente. En esta posición, se carga hasta que la diferencia de potencial entre las placas es V0. Acto seguido se abre el circuito y, sin descargar las placas, el recipiente es girado 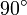 alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
Desprecie los efectos de borde y la influencia de las paredes.
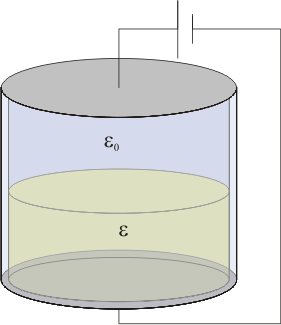
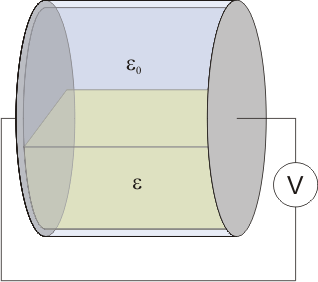
1.9 Cuatro conductores paralelos
Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado 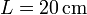 de lado y grosor
de lado y grosor 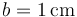 . Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo
. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo 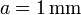 . El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad
. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad 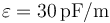 .
.
El conductor 1 y el 4 se encuentran permanentemente a tierra.
Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial 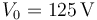 $, mientras que el 3 está aislado y descargado.
$, mientras que el 3 está aislado y descargado.
- Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores.
- Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras
- Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies?
- Halle la energía almacenada en el sistema antes y después de mover el interruptor.
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
2 Problemas adicionales
2.1 Esfera que se conecta a una fuente de tensión
Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga 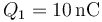 . Alrededor de la esfera no hay más conductores ni cargas.
. Alrededor de la esfera no hay más conductores ni cargas.
- Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
- Suponga que ahora se conecta a la esfera una fuente de tensión de 0.3 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
- Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
- ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
- Determine la ecuación diferencial que gobierna el potencial V(t) de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de V(t) frente al tiempo.
Dato: 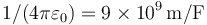
2.2 Carga en el interior de una corona esférica
Se tiene un conductor metálico en forma de corona esférica de radio interior 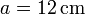 y exterior
y exterior 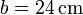 . En el centro de la
cavidad esférica se encuentra una carga puntual
. En el centro de la
cavidad esférica se encuentra una carga puntual 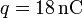 . Calcule:
. Calcule:
- La carga en cada uno de las superficies del conductor.
- El potencial al que se encuentra la carga y el conductor
- El campo eléctrico en el exterior de la esfera y en la cavidad.
- La energía electrostática almacenada.
para los siguientes cuatro casos:
- La corona esférica está conectada a tierra.
- La corona está aislada y descargada.
- La corona está conecta a una fuente de tensión que fija un voltaje
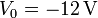 .
.
- La corona está aislada y almacena una carga
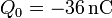 .
.
2.3 Esfera rodeada de corona esférica
Se tiene una esfera conductora de radio a que almacena una carga Q0. Rodeándola se halla una corona esférica también conductora de radio interior 2a y exterior 4a. Esta corona se halla inicialmente aislada y descargada.
- Calcule el campo eléctrico en todos los puntos del espacio. Puede suponerse que las distribuciones de carga son todas uniformes.
- Determine el potencial al que se encuentra la esfera interior.
- Calcule la energía electrostática almacenada en el sistema.
- Suponga que se conecta la corteza exterior a tierra. Una vez que se vuelve al equilibrio electrostático, ¿cómo cambia el potencial de la esfera interior y la energía almacenada? ¿A qué se debe la diferencia de energía?
2.4 Condensador plano de placas circulares
Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V.
Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa 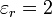 . ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
. ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
2.5 Cuatro placas conductoras paralelas
Se colocan paralelamente cuatro placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm, ésta de la tercera 0.4 mm, y esta de la cuarta 0.6 mm. Las dos placas centrales están aisladas y descargadas. Se coloca la primera placa a 100 V y la última a tierra. Halle el voltaje y la carga de cada placa, así como la energía almacenada.
Sin descargar las placas se desconecta la fuente de tensión. A continuación se conecta por un hilo metálico la segunda con la tercera placa. Halle las nuevas cargas, voltajes y energía almacenada.
¿Cómo cambian los resultados se conectan las placas centrales sin desconectar previamente la fuente de tensión? ¿Qué trabajo realiza la fuente en este caso?
2.6 Condensador que se rellena parcialmente de dieléctrico
El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.
Entre las placas se establece una diferencia de potencial de 20 V
- ¿Cuánto vale la energía almacenada en el sistema?
- Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (
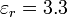 ) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
- Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?
2.7 Capacidad de la tierra y la ionosfera
La tierra y la ionosfera pueden considerarse que forman un condensador esférico. Si el radio de la tierra es de aproximadamente 6400 km y la ionosfera está a 100 km de altura, ¿cuánto vale la capacidad de este condensador?
2.8 Sistema con tres conductores esféricos
En una esfera metálica de radio 36 mm se han hecho dos cavidades, también esféricas, de radio 18 mm. Concéntricas con cada una de estos huecos se hallan sendas esferas metálicas de radio 9 mm. No hay más conductores en el sistema. Suponga que la esfera exterior se encuentra aislada y descargada; una de las esferas interiores se encuentra a un potencial 8 kV y la otra se encuentra a tierra.
- ¿Cuál es la carga en cada conductor? ¿Y el potencial?
- Halle la energía almacenada en el sistema.
- Si tomamos como eje OX el que pasa por los tres centros y origen O el centro del sistema, calcule el módulo del campo eléctrico en las siguientes posiciones
| x (mm) | 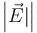
|
|---|---|
| −16 | |
| −8 | |
| +8 | |
| +16 | |
| +24 | |
| +28 |
2.9 Dos esferas conductoras dentro de otra
Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36 mm y 18 mm. En el centro de cada hueco se encuentran sendas esferas metálicas de radio 12 mm, siendo “1” la que está en el hueco grande y “3” la que está en el pequeño. Entre las esferas hay vacío y no hay más conductores ni cargas en el sistema.
Inicialmente la esfera “1” contiene una carga 120 nC mientras que los otros dos conductores están aislados y descargados.
- Halle el potencial de cada conductor, así como la energía almacenada en el sistema.
- Se conectan las dos esferas interiores mediante un hilo de resistencia 1 kΩ. Una vez que se ha vuelto a alcanzar el estado final, ¿cuáles son los nuevos potenciales de los conductores?
- ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia?
- Halle la potencia instantánea disipada en el cable justo tras la conexión.
Tómese
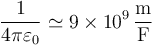
==Tres superficies conductoras concéntricas Se tiene un sistema formado por tres superficies conductoras esféricas concéntricas, de radios 2b, 3b y 6b. Inicialmente la esfera interior almacena una carga − Q0, la intermedia está aislada y descargada y la exterior almacena una carga + Q0.

- Calcule el potencial al que se encuentra cada esfera.
- Halle el campo eléctrico en los puntos del eje OZ siguientes: z = 0, z = 5b / 2, z = 4b y z = 8b, siendo el origen de coordenadas el centro de las esferas.
- Halle la energía almacenada en el sistema
En un momento dado se cierra el interruptor que conecta la esfera intermedia a tierra. Una vez que se alcanza de nuevo el equilibrio electrostático:
- ¿Cuáles son las nuevas cargas y potenciales de los tres conductores?
- ¿Cuánto vale ahora el campo eléctrico en los puntos del apartado 2?
- ¿Cuánto vale la energía almacenada en el sistema?
- ¿Cuánta energía se ha perdido en el proceso?
3 Preguntas de test
3.1 Asociación de tres condensadores
Dado el sistema de tres condensadores de la figura,
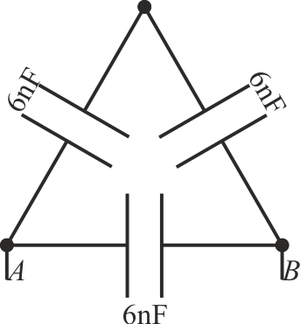
¿cuánto vale la capacidad equivalente entre A y B?
- A 2 nF.
- B 9 nF.
- C 4 nF.
- D 18 nF.
3.2 Reparto de carga entre dos esferas
Dos esferas metálicas de 30 cm y 10 cm de radio están muy alejadas. La primera tiene una carga de 10 nC y la segunda está descargada. Se conectan por un hilo metálico. ¿Cómo se reparte la carga entre la grande y la pequeña?
- A 50% - 50%
- B 90% - 10%
- C 75% - 25%
- D 100% - 0%
3.3 Sistema de tres conductores
Se tiene el sistema de conductores en equilibrio electrostático de la figura, en la que se han indicado algunas de las líneas de campo eléctrico
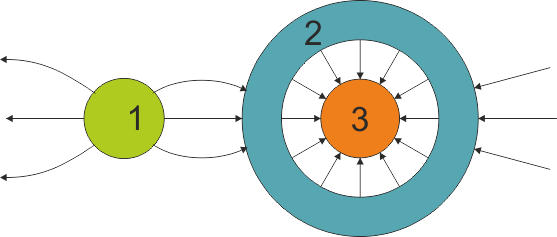
¿Qué podemos decir de los potenciales de cada conductor (tomando como origen de potencial el infinito)?
- A V1 > V2 > 0 > V3
- B Tal situación es imposible.
- C V1 > 0 > V2 > V3
- D V1 > V2 > V3 > 0
¿Cómo sería el sistema de condensadores que representa a este sistema de conductores?
| 
|
| A | B |
|---|---|
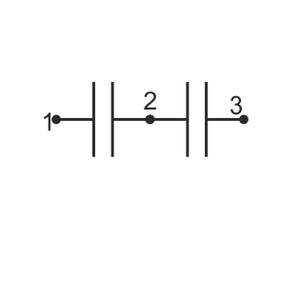
| 
|
| C | D |
3.4 Condensador con dieléctrico
Se tiene un condensador plano formado por dos placas circulares de radio 10 cm separadas una distancia de 1 mm. Entre ellas hay una lámina de dieléctrico de permitividad 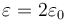 . La lámina llena todo el espacio entre las placas. Se aplica entre las placas una diferencia de potencial de 100 V
. La lámina llena todo el espacio entre las placas. Se aplica entre las placas una diferencia de potencial de 100 V
¿Cuánto vale la energía almacenada en el sistema?
- A 2.78 μJ.
- B 0.556 nJ.
- C 1.39 μJ.
- D 5.56 μJ.
Sin desconectar la fuente se retira la lámina de dieléctrico. En este proceso la energía almacenada…
- A aumenta al cuádruple.
- B aumenta al doble.
- C se reduce a la mitad.
- D se queda igual.
3.5 Condensador relleno de papel
Se construye un condensador plano colocando horizontalmente un disco de radio 10 cm, sobre él una hoja de papel de 0.1 mm de espesor con permitividad 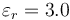 y sobre ésta se apoya otro disco metálico del mismo radio.
y sobre ésta se apoya otro disco metálico del mismo radio.
¿Cuánto vale la capacidad del condensador resultante?
- A 0.085 pF.
- B 8.34 nF.
- C 2.78 nF.
- D 26.6 nF.
La placa superior se eleva una distancia de 0.1 mm, separándola del papel, ¿cuánto vale la nueva capacidad del condensador?
- A 4.17 nF.
- B 11.12 nF
- C 2.09 nF.
- D 16.7 nF
3.6 Carga frente a esfera
Una esfera conductora se encuentra conectada a tierra. Frente a ella se coloca una carga puntual positiva. ¿Como son el potencial y la carga de la esfera?
- A V = 0 y Q < 0
- B V = 0 y Q = 0
- C V > 0 y Q = 0
- D V > 0 y Q > 0
3.7 Dieléctrico con dos capas
Se tiene el condensador de la figura, formado por dos placas conductoras paralelas de sección S y distancia entre placas a. Entre ellas la mitad del espacio está ocupado por un dieléctrico ideal de permitividad relativa 1.5 y la otra mitad por uno de permitividad 3.0, siendo la frontera paralela a las placas. La capacidad del condensador en vacío en ausencia de los dieléctricos es C0.

¿Cuánto vale la capacidad de este condensador?
- A C = 4.5C0
- B C = 2.25C0
- C C = 0.5C0
- D C = 2.0C0
Suponga que este condensador se conecta a una fuente de tensión V0. Si E1 es el campo en el material de permitividad 1.5 y E2 en el de permitividad 3.0, ¿cómo se relacionan estos dos campos?
- A Puede darse cualquiera de las otras tres posibilidades.
- B E1 > E2
- C E1 < E2
- D E1 = E2
3.8 Dos conductores enfrentados
Se colocan dos conductores uno frente al otro. El primero tiene Q1 > 0 y el segundo Q2 = 0. No hay más cargas ni conductores en el sistema. ¿Qué podemos decir de sus potenciales?
- A V1 > 0, V2 < 0.
- B V1 > 0, V2 > 0.
- C V1 = 0, V2 < 0.
- D V1 > 0, V2 = 0.
3.9 Dos superficies esféricas
Se tienen dos superficies conductoras esféricas concéntricas, de radios 1 cm y 3 cm, respectivamente. Inicialmente la interior (1) almacena una carga de − 40 nC y la exterior (2) una de +20 nC.
¿Cuál de las siguientes figuras describe adecuadamente el campo eléctrico en el sistema?
| 
|
| A | B |
|---|---|
| 
|
| C | D |
Se conectan las dos esferas por un cable. Una vez que se alcanza el equilibrio electrostático, ¿cómo queda el reparto de cargas entre las dos?
- A
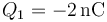 ,
, 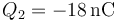
- B
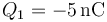 ,
, 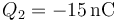
- C
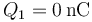 ,
, 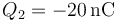
- D
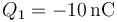 ,
, 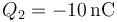
- A
3.10 Tres placas circulares
Tres placas conductoras circulares de radio 12 cm se encuentran situadas paralelamente con una distancia de 1 mm entre ellas. El espacio intermedio está vacío. La placa central se encuentra a un potencial de 100 V, mientras que las exteriores están puestas a tierra.
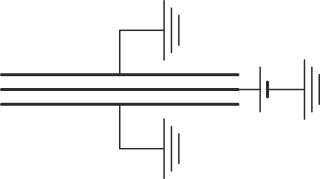
La energía electrostática almacenada en el sistema vale…
- A 4 μJ
- B 8 μJ
- C 2 μJ
- D 1 μJ
3.11 Comparación de dos condensadores
Se tienen dos condensadores planos de las mismas dimensiones (sección y espesor). El 1 está relleno de un dieléctrico con permitividad relativa 3.0 y el 2 de un dieléctrico con permitividad 1.5. En un momento dado, los dos están cargados con la misma carga Q0. ¿En cuál de ellos es mayor el campo eléctrico interior?
- A En el 2.
- B Vale lo mismo en los dos.
- C En el 1.
- D No hay suficiente información para saberlo.






