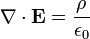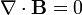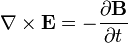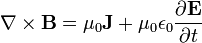Fundamentos matemáticos. Introducción
De Laplace
(Diferencias entre revisiones)
(→Enlaces) |
|||
| (16 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | <categorytree mode=pages depth="1">Fundamentos matemáticos</categorytree> | ||
| + | |||
==En este tema…== | ==En este tema…== | ||
| Línea 15: | Línea 17: | ||
El electromagnetismo, objeto de este curso, se resume en estas cuatro ecuaciones, denominadas ecuaciones de Maxwell: | El electromagnetismo, objeto de este curso, se resume en estas cuatro ecuaciones, denominadas ecuaciones de Maxwell: | ||
| - | + | * <math>\nabla \cdot \mathbf{E} = \frac {\rho} {\epsilon_0}</math> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | * <math>\nabla \cdot \mathbf{B} = 0</math> | |
| - | + | * <math>\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}</math> | |
| + | * <math>\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}} {\partial t}</math> | ||
| + | Sin embargo, antes de que podamos discutir su significado físico, necesitamos comprender el lenguaje en que están escritas, ¿qué representa <math>\nabla\times</math>? ¿Qué es un campo vectorial? ¿Por qué estas ecuaciones son suficientes y no hacen falta más? | ||
| - | + | Por ello, antes de entrar en materia, debemos entender los fundamentos matemáticos de la teoría electromagnética. Este tema es muy importante, ya que todo lo que se diga aquí, incluso los ejemplos, va a ser usado más tarde o más temprano a lo largo del curso. | |
| - | + | ==Enlaces== | |
| + | * '''Siguiente:''' [[Sistemas de coordenadas]] | ||
| - | + | [[Categoría:Fundamentos matemáticos|10]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
última version al 09:56 24 nov 2007
1 En este tema…
- Describimos y explicamos los sistemas de coordenadas.
- Introducimos el concepto de campo.
- Definimos los operadores vectoriales más importantes.
- Enunciamos los teoremas integrales más relevantes para el curso.
2 Introducción
El electromagnetismo, objeto de este curso, se resume en estas cuatro ecuaciones, denominadas ecuaciones de Maxwell:
Sin embargo, antes de que podamos discutir su significado físico, necesitamos comprender el lenguaje en que están escritas, ¿qué representa 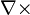 ? ¿Qué es un campo vectorial? ¿Por qué estas ecuaciones son suficientes y no hacen falta más?
? ¿Qué es un campo vectorial? ¿Por qué estas ecuaciones son suficientes y no hacen falta más?
Por ello, antes de entrar en materia, debemos entender los fundamentos matemáticos de la teoría electromagnética. Este tema es muy importante, ya que todo lo que se diga aquí, incluso los ejemplos, va a ser usado más tarde o más temprano a lo largo del curso.
3 Enlaces
- Siguiente: Sistemas de coordenadas