Problemas de corriente eléctrica (GIA)
De Laplace
(Diferencias entre revisiones)
(→Asociación de resistencia independiente de la temperatura) |
(→Determinación del material de un cable conductor) |
||
| (23 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | ==[[Asociación de resistencias independiente de la temperatura GIA|Asociación de | + | __toc__ |
| - | Un cable de cobre de sección transversal <math> | + | |
| + | ==[[Proceso de carga de una esfera conductora (F2GIA) | Proceso de carga de una esfera conductora]]== | ||
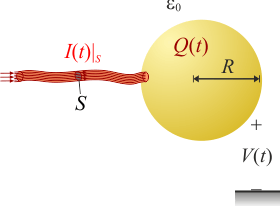
| + | [[Archivo:cuest_conserva_1.gif|right]]A una esfera metálica de radio <math>R</math>, inicialmente descargada, llega una corriente eléctrica a través de un delgado hilo conductor. La intensidad de la corriente decae exponencialmente en el tiempo según la ley <math>I(t)=I_0e^{-t/\tau}</math>, donde <math>I_0</math> es la intensidad de corriente inicial y <math>\tau</math> es un valor constante con dimensiones de tiempo (constante de relajación). ¿Cómo será el valor del potencial electrostático en la esfera al cabo de un tiempo suficientemente grande (<math>t\longrightarrow\infty</math>)? | ||
| + | |||
| + | ==[[Propiedades de corriente estacionaria en cable conductor (F2GIA) | Propiedades de una corriente estacionaria en un cable]]== | ||
| + | Un cable conductor cuya sección transversal tiene un área de <math>13.30\,\mathrm{mm}^2</math> transporta una corriente estacionaria de <math>2\,\mathrm{A}\,</math> durante 5 minutos. Considerando que el valor de la carga del electrón es <math>q_e=-1.6\times 10^{-19}\,\mathrm{C}\,</math>, calcule: | ||
| + | |||
| + | # Carga total y número de electrones que atraviesan cualquier sección transversal del cable en ese tiempo. | ||
| + | # Tiempo que tarda un electrón en recorrer una distancia de <math>1\,\mathrm{cm}\,</math> sabiendo que el material posee una densidad numérica de electrones libres <math>n^-=8.5\times 10^{28}\,\mathrm{m}^{-3}</math>. | ||
| + | |||
| + | ==[[Determinación del material de un cable conductor (GIA) | Determinación del material de un cable conductor]]== | ||
| + | Un conductor filiforme, de un material desconocido, tiene una | ||
| + | sección uniforme de área <math>S= 2\,\mathrm{mm}^2=2\times | ||
| + | 10^{-2}\,\mathrm{cm}^2</math>. Para determinar el tipo de material, se hace | ||
| + | que por el hilo conductor circule una corriente estacionaria de | ||
| + | intensidad <math>I_0=2\,\mathrm{A}</math> y, con la ayuda de un voltímetro, | ||
| + | se determinan dos puntos ''A'' y ''B'' en el hilo tales que la diferencia | ||
| + | de potencial entre ellos sea <math>V_A-V_B=3\,\mathrm{mV}</math>. Se determina que la longitud del hilo comprendida entre dichos puntos es <math>L_{AB}=11,4\,\mathrm{cm}</math>. | ||
| + | |||
| + | # Calcule la conductividad del hilo e indique de qué material está fabricado. | ||
| + | # Haga una estimación de los valores de la intensidad del campo eléctrico (<math>E=|\vec{E}|</math>), y de la densidad volumétrica (<math>J=|\vec{J}|</math>), en el interior del cable. | ||
| + | |||
| + | ==[[Calefactor_de_corriente_eléctrica,_F2_GIA_(Abr,_2013)| Calefactor eléctrico]]== | ||
| + | Se pretende diseñar un sistema calefactor consistente en un recipiente en cuyo interior hay un cable de hierro de sección <math>0.32\,\mathrm{mm}^2</math>, y cuya resistividad a <math>20^\mathrm{o}\mathrm{C}</math> es <math>\rho_0\approx 10^{-7}\,\Omega\!\ \mathrm{m}</math>. Los extremos del cable se conectan a los electrodos de un generador de continua, entre los que existe una diferencia de potencial invariable de <math>100\,\mathrm{V}</math>, dando lugar a que el cable sea recorrido por una corriente eléctrica. El calor que se desprende por efecto Joule se utiliza para calentar el agua contenida en el recipiente, desde la temperatura ambiente (en torno a <math>20^\mathrm{o}\mathrm{C}</math>) hasta la de | ||
| + | ebullición a <math>100^\mathrm{o}\mathrm{C}</math>. Cuando se realiza dicho proceso de calentamiento, se observa que la intensidad de la corriente al final del mismo es el <math>70\%</math> de la inicial. | ||
| + | |||
| + | # ¿Cuál es el valor del coeficiente <math>\alpha</math> de variación de la resistividad del hierro con la temperatura, si la longitud y sección del cable no sufren variaciones apreciables? | ||
| + | # Si el generador sólo puede suministrar una potencia máxima de <math>750\,\mathrm{w}</math>, ¿qué limitaciones debe cumplir la longitud del cable? | ||
| + | |||
| + | |||
| + | ==[[Intensidad de corriente máxima en un fusible de plomo (F2GIA) | Intensidad de corriente máxima en un fusible de plomo]]== | ||
| + | En un circuito eléctrico hay emplazado un ''fusible'' consistente en un hilo de plomo de <math>0.4\,\mathrm{mm}^2\,</math> de sección y <math>20\,\mathrm{mm}\,</math> de longitud que se funde cuando la intensidad de la corriente que circula por el circuito supera un determinado valor. Sabiendo que el plomo | ||
| + | funde a unos <math>320{}^o\,\mathrm{C}\,</math>, cuando el paso de la corriente eléctrica provoca una disipación de potencia por unidad de volumen de <math>0.7\,\mathrm{w/mm}^3</math>, y asumiendo que su resistividad varía linealmente con | ||
| + | la temperatura, ¿qué intensidad de corriente, aproximadamente, provocará la fusión del hilo de plomo? | ||
| + | |||
| + | '''Datos:''' resistividad del plomo a <math>T_0=20{}^o\,\mathrm{C}\,</math>, | ||
| + | <math>\rho_0=22\times 10^{-8}\,\Omega\mathrm{m}</math>; coeficiente de | ||
| + | temperatura, <math>\alpha=4.3\times 10^{-3}\,\mathrm{K}^{-1}</math>. | ||
| + | |||
| + | <center>[[Archivo:fusible_plomo_0.gif]]</center> | ||
| + | |||
| + | ==[[Conexiones serie y paralelo de bombillas a batería real GIA|Conexiones serie y paralelo de bombillas a una batería]]== | ||
| + | Se dispone de una batería de <math>12 \,\mathrm{V}\,</math> con una resistencia interna de <math>0,5\,\Omega</math> y de dos pequeñas bombillas iguales. Cada bombilla puede modelarse como una resistencia de <math>20\,\Omega</math>. | ||
| + | |||
| + | # Si se conectan ambas bombillas en serie a la batería, ¿cuál de ellas dará más luz? | ||
| + | # Si a continuación se conectan en paralelo, ¿iluminarán más o menos? | ||
| + | |||
| + | <center>[[Archivo:circuit_bomb_fem.gif]]</center> | ||
| + | ==[[Asociación de resistencias independiente de la temperatura GIA|Asociación de resistencias independiente de la temperatura]]== | ||
| + | Un cable de cobre de sección transversal <math>S</math> y longitud <math>l_\mathrm{Cu}</math> se conecta en serie con un cable de carbono de la misma sección transversal y longitud <math>l_\mathrm{C}</math>. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación | ||
sólo asegura independencia de la resistencia con la <math>R</math> con la temperatura para pequeñas variaciones de dicha magnitud. | sólo asegura independencia de la resistencia con la <math>R</math> con la temperatura para pequeñas variaciones de dicha magnitud. | ||
'''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>. | '''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>. | ||
| + | |||
| + | |||
| + | <center>[[Archivo:resit_no_temp_0.gif]]</center> | ||
| + | |||
| + | ==[[Barras_conductoras_en_paralelo,_F2_GIA_(Sept,_2012)|Barras conductoras en paralelo]]== | ||
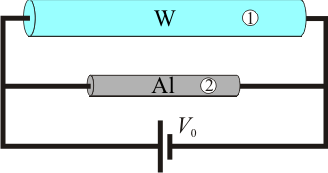
| + | [[Archivo:barras_paralelo_0.gif|right]]La longitud y el diámetro de una barra cilíndrica de wolframio o tungsteno (W) son el doble que los de otra barra de aluminio (Al). En ambos casos, la longitud de la barra es mucho mayor que su diámetro. Los extremos de ambas están conectados a los bornes o polos de una batería de fuerza electromotriz <math>V_0</math> y resistencia interna despreciable, constituyendo una asociación de resistencias ''en paralelo''. Sabiendo que la conductividad eléctrica del aluminio es prácticamente el doble que la del tungsteno, determine las relaciones entre las siguientes magnitudes: | ||
| + | |||
| + | # Resistencias eléctricas de las barras e intensidades de corriente. | ||
| + | # Densidad de corriente e intensidad del campo eléctrico en el interior de los conductores. | ||
| + | |||
| + | |||
| + | |||
| + | [[Categoría:Problemas de corriente eléctrica F2 GIA]] | ||
última version al 18:24 16 jul 2018
1 Proceso de carga de una esfera conductora
)?
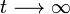2 Propiedades de una corriente estacionaria en un cable
Un cable conductor cuya sección transversal tiene un área de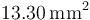 
transporta una corriente estacionaria de 
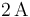durante 5 minutos. Considerando que el valor de la carga del electrón es 
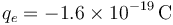, calcule:
- Carga total y número de electrones que atraviesan cualquier sección transversal del cable en ese tiempo.
- Tiempo que tarda un electrón en recorrer una distancia de
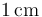sabiendo que el material posee una densidad numérica de electrones libres 
.
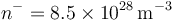3 Determinación del material de un cable conductor
Un conductor filiforme, de un material desconocido, tiene una
sección uniforme de área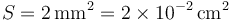 
. Para determinar el tipo de material, se hace
que por el hilo conductor circule una corriente estacionaria de
intensidad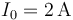 
y, con la ayuda de un voltímetro,
se determinan dos puntos A y B en el hilo tales que la diferencia
de potencial entre ellos sea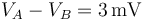 
. Se determina que la longitud del hilo comprendida entre dichos puntos es 
.
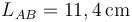- Calcule la conductividad del hilo e indique de qué material está fabricado.
- Haga una estimación de los valores de la intensidad del campo eléctrico (
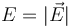), y de la densidad volumétrica (
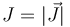), en el interior del cable.
4 Calefactor eléctrico
Se pretende diseñar un sistema calefactor consistente en un recipiente en cuyo interior hay un cable de hierro de sección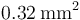 
, y cuya resistividad a 20oC es 
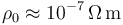. Los extremos del cable se conectan a los electrodos de un generador de continua, entre los que existe una diferencia de potencial invariable de 
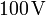, dando lugar a que el cable sea recorrido por una corriente eléctrica. El calor que se desprende por efecto Joule se utiliza para calentar el agua contenida en el recipiente, desde la temperatura ambiente (en torno a 20oC) hasta la de
ebullición a 100oC. Cuando se realiza dicho proceso de calentamiento, se observa que la intensidad de la corriente al final del mismo es el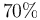 
de la inicial.
- ¿Cuál es el valor del coeficiente α de variación de la resistividad del hierro con la temperatura, si la longitud y sección del cable no sufren variaciones apreciables?
- Si el generador sólo puede suministrar una potencia máxima de
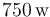, ¿qué limitaciones debe cumplir la longitud del cable?
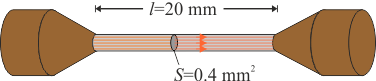
5 Intensidad de corriente máxima en un fusible de plomo
En un circuito eléctrico hay emplazado un fusible consistente en un hilo de plomo de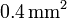 
de sección y 
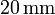de longitud que se funde cuando la intensidad de la corriente que circula por el circuito supera un determinado valor. Sabiendo que el plomo
funde a unos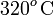 
, cuando el paso de la corriente eléctrica provoca una disipación de potencia por unidad de volumen de 
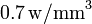, y asumiendo que su resistividad varía linealmente con
la temperatura, ¿qué intensidad de corriente, aproximadamente, provocará la fusión del hilo de plomo?
Datos: resistividad del plomo a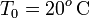 
,
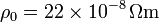; coeficiente de
temperatura,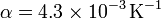 
.
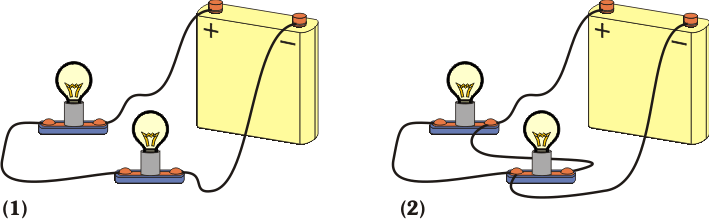
6 Conexiones serie y paralelo de bombillas a una batería
Se dispone de una batería de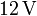 
con una resistencia interna de 
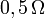y de dos pequeñas bombillas iguales. Cada bombilla puede modelarse como una resistencia de 
.
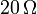- Si se conectan ambas bombillas en serie a la batería, ¿cuál de ellas dará más luz?
- Si a continuación se conectan en paralelo, ¿iluminarán más o menos?
7 Asociación de resistencias independiente de la temperatura
Un cable de cobre de sección transversal S y longitud lCu se conecta en serie con un cable de carbono de la misma sección transversal y longitud lC. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación sólo asegura independencia de la resistencia con la R con la temperatura para pequeñas variaciones de dicha magnitud.
Datos: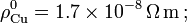 
.
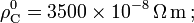
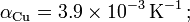
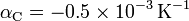8 Barras conductoras en paralelo
- Resistencias eléctricas de las barras e intensidades de corriente.
- Densidad de corriente e intensidad del campo eléctrico en el interior de los conductores.
