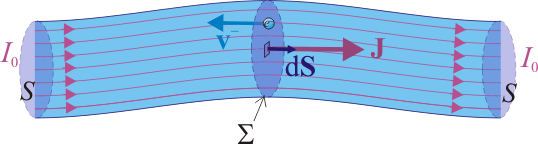
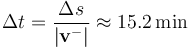Propiedades de corriente estacionaria en cable conductor (F2GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Carga que atraviesa las secciones transversales
- 2.2 Celeridad de los electrones

1 Enunciado

Un cable conductor cuya sección transversal tiene un área de 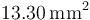$13.30\,\mathrm{mm}^2$ transporta una corriente estacionaria de 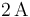$2\,\mathrm{A}\,$ durante 5 minutos. Considerando que el valor de la carga del electrón es 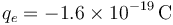$q_e=-1.6\times 10^{-19}\,\mathrm{C}\,$ , calcule:

Carga total y número de electrones que atraviesan cualquier sección transversal del cable en ese tiempo.
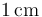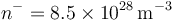Tiempo que tarda un electrón en recorrer una distancia de $1\,\mathrm{cm}\,$ sabiendo que el material posee una densidad numérica de electrones libres $n^-=8.5\times 10^{28}\,\mathrm{m}^{-3}$ .

2 Solución

Como se sabe, la intensidad de corriente estacionaria $I 0$ es el flujo de la densidad volumétrica de corriente a través de las superficies equipotenciales que hay en el cable, cuando entre sus extremos se establece una determinada diferencia de potencial:

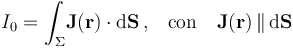
$I_0=\int_\Sigma\!\mathbf{J}(\mathbf{r})\cdot\mathrm{d}\mathbf{S}\,\mathrm{,}\quad\mathrm{con}\quad \mathbf{J}(\mathbf{r})\!\ \| \!\ \mathrm{d}\mathbf{S}$

2.1 Carga que atraviesa las secciones transversales

Si el cable se aproxima al modelo de conductor filiforme, las superficies equipotenciales a través de las que fluye la intensidad máxima de corriente coinciden con las secciones transversales del cable. Por otra parte, dicha intensidad de corriente describe la cantidad neta de carga eléctrica positiva que por unidad de tiempo cruza cada sección tranversal en el sentido de 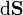$\mathrm{d}\mathbf{S}$ , y/o la cantidad neta de carga negativa que por unidad de tiempo pasa en sentido contrario al de aquél vector. Y como la intensidad de la corriente estacionaria es constante, la relación entre la cantidad de carga que cruza la superficie y el intervalo de tiempo empleado, es independiente de la duración de dicho intervalo:

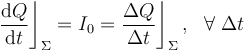
$\frac{\mathrm{d}Q}{\mathrm{d}t}\bigg\rfloor_\Sigma=I_0=\frac{\Delta Q}{\Delta t}\bigg\rfloor_\Sigma\,\mathrm{,}\;\;\;\forall\;\Delta t$

En consecuencia, una intensidad constante de 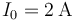$I_0=2\,\mathrm{A}\,$ fluyendo durante un intervalo de 5 minutos, o lo que es lo mismo, 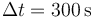$\Delta t=300\,\mathrm{s}$ , da lugar a que la cantidad total de carga que fluye a través de las secciones transversales es:

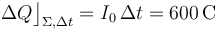
$\Delta Q\big\rfloor_{\Sigma,\Delta t}=I_0\!\ \Delta t=600\,\mathrm{C}$

Como se sabe, los cables conductores se construyen con materiales metálicos, donde las corrientes eléctricas de conducción están constituidas por electrones (casi)libres en movimiento. El promedio de electrones libres 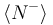$\langle N^-\rangle$ que fluyen a tráves de las superficies equipotenciales en 5 minutos, será:

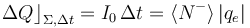
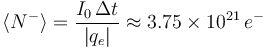
$\Delta Q\big\rfloor_{\Sigma,\Delta t}=I_0\!\ \Delta t=\langle N^-\rangle\!\ |q_e|$ $\Rightarrow$ $\langle N^-\rangle=\frac{I_0\!\ \Delta t}{|q_e|}\approx 3.75\times 10^{21}\,e^-$

2.2 Celeridad de los electrones

La densidad volumétrica de corriente en el cable es debida sólo a portadores con carga negativa: los electrones libres. Por tanto, se tendrá que:

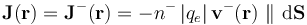
$\mathbf{J}(\mathbf{r})=\mathbf{J}^-(\mathbf{r})=-n^-\!\ |q_e|\!\ \mathbf{v}^-(\mathbf{r})\ \|\ \mathrm{d}\mathbf{S}$

donde $n -$ es la densidad promedio de electrones libres en el cable conductor (que será la misma en todos los puntos), y 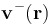$\mathbf{v}^-(\mathbf{r})$ la velocidad de arrastre de dichos electrones. El módulo de este vector será la celeridad a que, en promedio se desplaza la nube electrónica a lo largo del cable conductor cuando éste soporta la intensidad de corriente $I 0$ . Hay que tener en cuenta que dicha velocidad tiene sentido opuesto a la densidad volumétrica de corriente y al sentido de 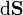$\mathrm{d}\mathbf{S}$ , en que se mide la corriente:

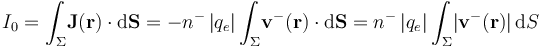
$I_0=\int_\Sigma\!\mathbf{J}(\mathbf{r})\cdot\mathrm{d}\mathbf{S}=-n^-\!\ |q_e|\int_\Sigma\! \mathbf{v}^-(\mathbf{r})\cdot\mathrm{d}\mathbf{S}=n^-\!\ |q_e|\int_\Sigma\! |\mathbf{v}^-(\mathbf{r})|\!\ \mathrm{d}S$

Y dado que el cable es un conductor filiforme, el área $S$ de su sección es los suficientemente pequeña como para considerar que la velocidad de arrastre para los electrones libres es, en buena aproximación, la misma en todos sus puntos. Se tendrá, por tanto:

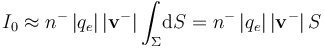
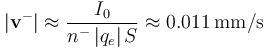
$I_0\approx n^-\!\ |q_e| \!\ |\mathbf{v}^-|\int_\Sigma\! \mathrm{d}S=n^-\!\ |q_e| \!\ |\mathbf{v}^-|\!\ S$ $\Rightarrow$ $|\mathbf{v}^-|\approx \frac{I_0}{n^-\!\ |q_e| \!\ S}\approx 0.011\,\mathrm{mm/s}\,$

El intervalo de tiempo necesario para que la nube de electrones libres recorra una distancia 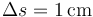$\Delta s=1\,\mathrm{cm}\,$ es:

$\Delta t=\frac{\Delta s}{|\mathbf{v}^-|}\approx 15.2\,\mathrm{min}\,$

Propiedades de corriente estacionaria en cable conductor (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Carga que atraviesa las secciones transversales

2.2 Celeridad de los electrones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES