Asociación de resistencias independiente de la temperatura GIA
De Laplace
1 Enunciado
Un cable de cobre de sección transversal S y longitud lCu se conecta en serie con un cable de carbono de la misma sección transversal y longitud lC. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación sólo asegura independencia de la resistencia con la R con la temperatura para pequeñas variaciones de dicha magnitud.
Datos: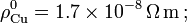 
.
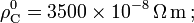
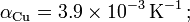
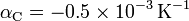2 Solución
La resistencia eléctrica R de esta asociación es igual a la relación entre la diferencia de potencial que se establece entre las superficies equipotenciales de los extremos A y B, y la intensidad de corriente que circula por los medios óhmicos. Por otra parte, si consideramos la superficie equipotencial C donde se conectan los dos medios óhmicos, podemos obtener la relación entre la resisencia equivalente del sistema y las resistencia eléctricas de los tubos de corriente que se forman en cada uno de los medios:
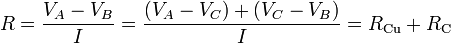
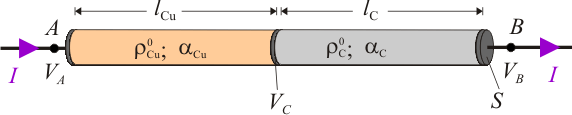
Si la sección S de los conductores es lo suficientemente pequeña frente a su longitud, o si los conductores son rectos, con sección constante, en cada uno de ellos las líneas de corriente serán paralelas. En esta situación, la resistencia eléctrica de cada medio es directamente proporcional a su longitud e inversamente proporcional a su sección, siendo la resistividad eléctrica del medio la constante de proporcionalidad. Y para variaciones moderadas de la temparatura, la resistividad eléctrica de los materiales conductores es una función lineal de la temperatura, de manera que:
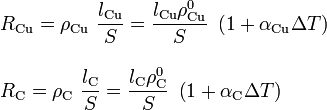
donde ρ0 y α son constantes características para cada medio, medidas a una temperatura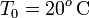 
, y ΔT la diferencia entre la temperatura de operación T y la de referencia T0
En consecuencia, la resistencia eléctrica del sistema conductor compuesto, en términos de las características físicas y geométricas de los medios óhmicos que lo constituyen es:
![R(T)=\frac{1}{S}\ \left[\rho_\mathrm{Cu}^0l_\mathrm{Cu}+\rho_\mathrm{C}^0l_\mathrm{C}+\left(\alpha_\mathrm{Cu}\rho_\mathrm{Cu}^0l_\mathrm{Cu}+\alpha_\mathrm{C}\rho_\mathrm{C}^0l_\mathrm{C}\right)(T-T_0)\right]](/wiki/images/math/4/8/0/480af05a81524cdc139b2022fae769a4.png)
Y para que no sea función de la temperatura, el factor que multiplica al incremento ΔT, deberá ser nulo.
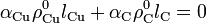
Obsérvese que, como resistividades y longitudes son siempre cantidades positivas, para que se verique la anterior relación (y por tanto, para conseguir que la resistencia de la asociación en serie no dependa de la temparatura), es necesario que los coeficientes alpha de los materiales sean tengan distinto signo. Es decir, que mientras que en uno de los materiales la resitividad debe crecer el aumento de la temperatura, en el otro debe disminuir. Y efectivamente esto ocurre si los materiales son cobre y grafito (carbono).
Sustituyendo los valores de los parámetros físicos se obtiene qué relación deben cumplir las longitudes de los dos medios óhmicos:
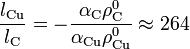
Obviamente, esto la resistencia de la asociación será independiente de la temperatura siempre que los valores de esta magnitud se encuentren dentro del rango de validez para el comportamiento lineal de las resistividades. Además, si la temperatura es muy elevada habría que tener en cuenta también que la dilatación de los materiales daría lugar a un alargamiento de los conductores y, por tanto, a un incremento extra de las resistencias.
