Problemas de electrostática en el vacío (GIE)
De Laplace
(Página creada con 'Calcule la carga total de las siguientes distribuciones de carga: N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con …') |
|||
| Línea 1: | Línea 1: | ||
| - | Calcule la carga total de las siguientes distribuciones de | + | ==[[Cálculos de carga total, campo y potencial]]== |
| - | carga: | + | Calcule la carga total de las siguientes distribuciones de carga: |
| - | + | # <math>N</math> cargas de valor <math>q</math> situadas en los vértices de un polígono | |
| - | regular de N lados situado en el plano XY, con centro el origen y | + | regular de <math>N</math> lados situado en el plano <math>XY</math>, con centro el origen y |
| - | cuyo primer vértice se encuentra en \vec{r}_1=a\vec{\imath}. | + | cuyo primer vértice se encuentra en <math>\vec{r}_1=a\vec{\imath</math>}. |
| - | + | # Un anillo circular de radio <math>R</math> con una densidad lineal de carga uniforme <math>\lambda_0</math>. | |
| - | uniforme \lambda_0. | + | # Un anillo circular de radio <math>R</math> con centro el origen y situado en el plano <math>XY</math>, con una densidad lineal de carga |
| - | + | <math>\lambda(\varphi)=\lambda_0\cos(\varphi)</math>, siendo <math>\varphi</math> el ángulo del vector de posición con el eje <math>OX</math>. | |
| - | en el plano XY, con una densidad lineal de carga | + | # Una superficie esférica de radio <math>a</math> con una densidad de carga uniforme <math>\sigma_0</math>, rodeada por una superficie esférica concéntrica de radio <math>b</math> con densidad de carga <math>-\sigma_0</math>. |
| - | \lambda(\varphi)=\lambda_0\cos(\varphi), siendo \varphi el ángulo | + | # Una esfera maciza de radio <math>R</math> con densidad de carga uniforme <math>\rho_0</math>. |
| - | del vector de posición con el eje OX. | + | # Una esfera maciza de radio <math>R</math> con una densidad de carga dependiente de la distancia al centro como |
| - | + | ||
| - | uniforme \sigma_0, rodeada por una superficie esférica concéntrica | + | |
| - | de radio b con densidad de carga -\sigma_0. | + | |
| - | + | ||
| - | \rho_0. | + | |
| - | + | ||
| - | dependiente de la distancia al centro como | + | |
<center><math> | <center><math> | ||
\rho(r) = A(R-2r)\qquad\qquad (r < R) | \rho(r) = A(R-2r)\qquad\qquad (r < R) | ||
</center></math> | </center></math> | ||
| - | |||
| + | Calcule el campo y el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema | ||
| - | + | ==[[Campo de dos cargas]]== | |
| - | + | Se tienen dos cargas <math>q_1</math> y <math>q_2</math> situadas respectivamente en los puntos <math>\vec{r}_1=-12\,\vec{\imath}\,(\mathrm{cm})</math> y | |
| - | los puntos \vec{r}_1=-12\,\vec{\imath}\,(\mathrm{cm}) y | + | <math>\vec{r}_2=+12\,\vec{\imath}\,(\mathrm{cm})</math>. Halle el campo eléctrico en los puntos |
| - | \vec{r}_2=+12\,\vec{\imath}\,(\mathrm{cm}). Halle el campo | + | |
| - | eléctrico en los puntos | + | |
<center><math> | <center><math> | ||
\vec{r}_A=\vec{0}\qquad \vec{r}_B=+9\vec{\jmath}\qquad | \vec{r}_A=\vec{0}\qquad \vec{r}_B=+9\vec{\jmath}\qquad | ||
| Línea 35: | Línea 26: | ||
(todas las distancias en cm) para los cuatro casos siguientes | (todas las distancias en cm) para los cuatro casos siguientes | ||
| + | # <math>q_1=q_2 = +1\,\mathrm{nC}</math> | ||
| + | # <math>q_1= +1\,\mathrm{nC}</math>, <math>q_2=-1\,\mathrm{nC}</math> | ||
| + | # <math>q_1= +1\,\mathrm{nC}</math>, <math>q_2=+9\,\mathrm{nC}</math> | ||
| + | # <math>q_1= +1\,\mathrm{nC}</math>, <math>q_2=-9\,\mathrm{nC}</math> | ||
| - | + | Para los cuatro pares de cargas, localice el punto del eje OX en que se anula el campo eléctrico. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Calcule el potencial eléctrico para todos los casos en todos los puntos indicados. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ==[[Campo de distribuciones con simetría esférica]]== | |
| - | + | Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica: | |
| - | todos los puntos del espacio para las siguientes distribuciones con | + | |
| - | simetría esférica: | + | |
| - | + | # Una superficie esférica de radio <math>a</math> que almacena una carga <math>Q</math> distribuida uniformemente. | |
| - | distribuida uniformemente. | + | # Dos superficies esféricas concéntricas, de radios <math>a</math> y <math>b</math> (<math>a<b</math>) que almacenan respectivamente cargas <math>+Q</math> y <math>-Q</math>, distribuidas uniformemente. |
| - | + | # Dos superficies esféricas concéntricas, de radios <math>a</math> y <math>b</math> (<math>a<</math>b) cargadas respectivamente con densidades superficiales | |
| - | (a<b) que almacenan respectivamente cargas +Q y -Q, | + | uniformes <math>+\sigma_0</math> y <math>-\sigma_0</math>. |
| - | distribuidas uniformemente. | + | # Una esfera maciza de radio <math>R</math> que almacena una carga <math>Q</math> distribuida uniformemente en su volumen. |
| - | + | # Una esfera maciza de radio <math>R</math> con una densidad de carga dependiente de la distancia al centro como | |
| - | (a<b) cargadas respectivamente con densidades superficiales | + | |
| - | uniformes +\sigma_0 y -\sigma_0. | + | |
| - | + | ||
| - | distribuida uniformemente en su volumen. | + | |
| - | + | ||
| - | dependiente de la distancia al centro como | + | |
<center><math> | <center><math> | ||
\rho(r) = A(R-2r)\qquad\qquad (r < R) | \rho(r) = A(R-2r)\qquad\qquad (r < R) | ||
</center></math> | </center></math> | ||
| - | |||
| + | ==[[Campo y potencial de una esfera con hueco]]== | ||
| + | Se tiene una carga <math>Q=14\,\mathrm{nC}</math> distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 cm de la esfera grande. | ||
| + | # Demuestre que el campo en el interior de la cavidad es uniforme y halle su valor. | ||
| + | # Calcule el valor del campo en el exterior de la esfera en un punto situado sobre la recta que une los dos centros, a una distancia de 25 cm del centro de la esfera grande. | ||
| + | # Calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros. | ||
| - | + | ==[[Campo eléctrico de un anillo y un disco]]== | |
| - | en | + | Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio <math>R</math> que almacena una carga <math>Q</math> distribuida |
| - | + | uniformemente. | |
| - | + | ||
| - | + | A partir del resultado anterior calcule el campo en los puntos del eje de un disco circular de radio <math>R</math>, en el cual existe una carga <math>Q</math> distribuida | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | eje de un | + | |
uniformemente. | uniformemente. | ||
| - | + | ==[[Campo eléctrico de un plano y de dos planos]]== | |
| - | + | Empleando el resultado del [[Campo eléctrico de un anillo y un disco|disco]], halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga <math>\sigma_0</math>. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | el campo eléctrico en cualquier punto del espacio debido a un plano | + | |
| - | infinito cargado uniformemente con una densidad de carga \sigma_0. | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Suponga que se tienen dos planos infinitos paralelos separados una distancia a que almacenan respectivamente densidades de carga <math>+\sigma_0</math> y <math>-\sigma_0</math>. | |
| - | + | ||
| - | + | ||
| - | + | Para el sistema de los dos planos, calcule la diferencia de potencial entre el plano cargado positivamente y el cargado negativamente. | |
| - | + | ||
| - | + | ==[[Potencial eléctrico debido a una superficie esférica]]== | |
| - | + | Halle el potencial eléctrico en todos los puntos del espacio creado por una carga <math>Q</math> distribuida uniformemente sobre una superficie esférica de radio <math>R</math>. | |
| - | + | ||
| - | + | ||
| + | ==[[Potencial eléctrico en el eje de un anillo]]== | ||
| + | Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia <math>z</math> al plano del anillo. | ||
| + | ¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo? | ||
| - | + | Supongamos que en lugar de una carga positiva tenemos una de −2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia <math>z= 1.0\,\mathrm{mm}</math> del centro del anillo, ¿qué tipo de movimiento describe esta carga? | |
| - | + | ||
| - | positiva | + | |
| - | + | ||
| - | + | ==[[Fuerza debida a un potencial eléctrico conocido]]== | |
| - | + | Considere que el potencial eléctrico a lo largo del eje <math>X</math> viene dado por la gráfica de la figura. Indique el sentido de la fuerza sobre una carga positiva sometida a este potencial. ¿Dónde es máxima esta fuerza en módulo? Si la carga se suelta en reposo en <math>x=0</math>, ¿qué tipo de movimiento describe? | |
| - | + | ¿Cómo cambian los resultados si la carga es negativa? | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ==[[Energía electrostática de un sistema de cargas puntuales]]== | |
| - | + | Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales: | |
| - | cargas puntuales: | + | |
| - | + | # <math>q_1=q_2=q_3=q_4=+60\,\mathrm{nC}</math>. | |
| - | + | # <math>q_1=q_2=q_3=q_4=-60\,\mathrm{nC}</math>. | |
| - | + | # <math>q_1=q_3=+60\,\mathrm{nC}</math>, <math>q_2=q_4=-60\,\mathrm{nC}</math>. | |
| - | + | # <math>q_1=q_2=+60\,\mathrm{nC}</math>, <math>q_3=q_4=-60\,\mathrm{nC}</math>. | |
| - | + | # <math>q_1=q_4=+60\,\mathrm{nC}</math>, <math>q_2=q_3=-60\,\mathrm{nC}</math>. | |
situadas en cada caso en los vértices de un rectángulo | situadas en cada caso en los vértices de un rectángulo | ||
| Línea 175: | Línea 99: | ||
4\vec{\jmath}\,\mathrm{cm} | 4\vec{\jmath}\,\mathrm{cm} | ||
</center></math> | </center></math> | ||
| - | |||
| - | + | ==[[Energía electrostática de superficies esféricas]]== | |
| - | + | Calcule la energía electrostática almacenada en las siguientes distribuciones de carga: | |
| - | distribuciones de carga: | + | |
| - | + | # Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga <math>Q</math>. | |
| - | uniformemente una carga Q. | + | # Dos superficies esféricas concéntricas de radios <math>a</math> y <math>b</math> (<math>a<b</math>) sobre las cuales hay distribuidas uniformemente cargas <math>+Q</math> y <math>-Q</math> respectivamente. |
| - | + | # Dos superficies esféricas concéntricas de radios <math>a</math> y <math>b</math> (<math>a<b</math>) sobre las cuales hay distribuidas cargas con densidades <math>+\sigma_0</math> y <math>-\sigma_0</math> respectivamente. | |
| - | las cuales hay distribuidas uniformemente cargas +Q y -Q respectivamente. | + | |
| - | + | ||
| - | las cuales hay distribuidas cargas con densidades +\sigma_0 y -\sigma_0 | + | |
| - | respectivamente. | + | |
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 19:19 12 abr 2012
1 Cálculos de carga total, campo y potencial
Calcule la carga total de las siguientes distribuciones de carga:
- N cargas de valor q situadas en los vértices de un polígono
regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{r}_1=a\vec{\imath }.
- Un anillo circular de radio R con una densidad lineal de carga uniforme λ0.
- Un anillo circular de radio R con centro el origen y situado en el plano XY, con una densidad lineal de carga
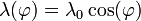 , siendo
, siendo  el ángulo del vector de posición con el eje OX.
el ángulo del vector de posición con el eje OX.
- Una superficie esférica de radio a con una densidad de carga uniforme σ0, rodeada por una superficie esférica concéntrica de radio b con densidad de carga − σ0.
- Una esfera maciza de radio R con densidad de carga uniforme ρ0.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como

Calcule el campo y el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema
2 Campo de dos cargas
Se tienen dos cargas q1 y q2 situadas respectivamente en los puntos 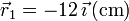 y
y
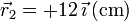 . Halle el campo eléctrico en los puntos
<center>
. Halle el campo eléctrico en los puntos
<center>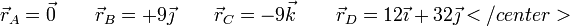 (todas las distancias en cm) para los cuatro casos siguientes
(todas las distancias en cm) para los cuatro casos siguientes
-
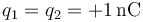
-
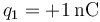 ,
, 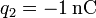
-
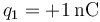 ,
, 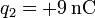
-
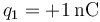 ,
, 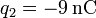
Para los cuatro pares de cargas, localice el punto del eje OX en que se anula el campo eléctrico.
Calcule el potencial eléctrico para todos los casos en todos los puntos indicados.
3 Campo de distribuciones con simetría esférica
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica:
- Una superficie esférica de radio a que almacena una carga Q distribuida uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) que almacenan respectivamente cargas + Q y − Q, distribuidas uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) cargadas respectivamente con densidades superficiales
uniformes + σ0 y − σ0.
- Una esfera maciza de radio R que almacena una carga Q distribuida uniformemente en su volumen.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como
<center>
4 Campo y potencial de una esfera con hueco
Se tiene una carga 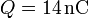 distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 cm de la esfera grande.
distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 cm de la esfera grande.
- Demuestre que el campo en el interior de la cavidad es uniforme y halle su valor.
- Calcule el valor del campo en el exterior de la esfera en un punto situado sobre la recta que une los dos centros, a una distancia de 25 cm del centro de la esfera grande.
- Calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.
5 Campo eléctrico de un anillo y un disco
Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio R que almacena una carga Q distribuida uniformemente.
A partir del resultado anterior calcule el campo en los puntos del eje de un disco circular de radio R, en el cual existe una carga Q distribuida uniformemente.
6 Campo eléctrico de un plano y de dos planos
Empleando el resultado del disco, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga σ0.
Suponga que se tienen dos planos infinitos paralelos separados una distancia a que almacenan respectivamente densidades de carga + σ0 y − σ0.
Para el sistema de los dos planos, calcule la diferencia de potencial entre el plano cargado positivamente y el cargado negativamente.
7 Potencial eléctrico debido a una superficie esférica
Halle el potencial eléctrico en todos los puntos del espacio creado por una carga Q distribuida uniformemente sobre una superficie esférica de radio R.
8 Potencial eléctrico en el eje de un anillo
Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia z al plano del anillo.
¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo?
Supongamos que en lugar de una carga positiva tenemos una de −2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia 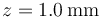 del centro del anillo, ¿qué tipo de movimiento describe esta carga?
del centro del anillo, ¿qué tipo de movimiento describe esta carga?
9 Fuerza debida a un potencial eléctrico conocido
Considere que el potencial eléctrico a lo largo del eje X viene dado por la gráfica de la figura. Indique el sentido de la fuerza sobre una carga positiva sometida a este potencial. ¿Dónde es máxima esta fuerza en módulo? Si la carga se suelta en reposo en x = 0, ¿qué tipo de movimiento describe?
¿Cómo cambian los resultados si la carga es negativa?
10 Energía electrostática de un sistema de cargas puntuales
Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales:
-
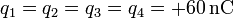 .
.
-
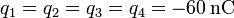 .
.
-
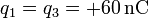 ,
,  .
.
-
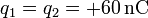 ,
, 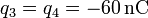 .
.
-
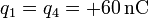 ,
, 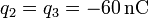 .
.
situadas en cada caso en los vértices de un rectángulo
<center>
11 Energía electrostática de superficies esféricas
Calcule la energía electrostática almacenada en las siguientes distribuciones de carga:
- Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga Q.
- Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas uniformemente cargas + Q y − Q respectivamente.
- Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas cargas con densidades + σ0 y − σ0 respectivamente.





