Problemas de Ondas sonoras
De Laplace
(→Duración de un trueno) |
|||
| (31 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==[[Duración de un trueno]]== |
Un rayo cae desde una nube situada a 2 km de altura. Si el rayo cae verticalmente e impacta de forma casi instantánea en un punto situado a 10 km de un observador, ¿cuánto tarda un el trueno en llegar a este observador? ¿Cuánto dura este trueno? Suponga que el aire se encuentra a 20 ºC. | Un rayo cae desde una nube situada a 2 km de altura. Si el rayo cae verticalmente e impacta de forma casi instantánea en un punto situado a 10 km de un observador, ¿cuánto tarda un el trueno en llegar a este observador? ¿Cuánto dura este trueno? Suponga que el aire se encuentra a 20 ºC. | ||
| - | + | [[Duración de un trueno|'''Solución''']] | |
| + | |||
| + | ==Onda sonora en agua== | ||
Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50 metros. El sistema emite un haz de ondas de sonido de frecuencia ''f'' = 262 Hz que forma un ángulo de 30º con la superficie del mar y mide el tiempo que tarda la onda, que se refleja en un pecio, en regresar al detector. Sabiendo que el tiempo de retardo es 0.135 segundos y que la densidad del agua es 1.06×10³ kg/m³, calcule | Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50 metros. El sistema emite un haz de ondas de sonido de frecuencia ''f'' = 262 Hz que forma un ángulo de 30º con la superficie del mar y mide el tiempo que tarda la onda, que se refleja en un pecio, en regresar al detector. Sabiendo que el tiempo de retardo es 0.135 segundos y que la densidad del agua es 1.06×10³ kg/m³, calcule | ||
| - | # | + | # La velocidad del sonido en el agua |
| - | # | + | # El módulo de compresibilidad del agua |
| - | # | + | # La longitud de onda de la señal emitida. |
| + | |||
| + | ==[[Tiempo de un sonido para llegar al suelo]]== | ||
| + | La temperatura de la atmósfera en sus capas bajas decrece con la altura como | ||
| + | |||
| + | <center><math>T(^\circ\mathrm{C}) = T_0-kz\,</math>{{qquad}}{{qquad}}<math> T_0 = 20\,^\circ\mathrm{C}</math>{{qquad}}{{qquad}}<math> k = 6\,\frac{^\circ\mathrm{C}}{\mathrm{km}}</math></center> | ||
| + | |||
| + | Un avión rompe la barrera del sonido cuando se encuentra a 8 km de altura. ¿Cuánto tarda el estampido sónico en llegar al suelo? | ||
| + | |||
| + | [[Tiempo de un sonido para llegar al suelo|'''Solución''']] | ||
| + | |||
| + | ==Batidos por diferencia de temperaturas== | ||
| + | Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC. Admita que la velocidad del sonido en el aire a temperaturas próximas a la ambiente depende de la temperatura como | ||
| + | |||
| + | <center><math>c = 331\,\frac{\mathrm{m}}{\mathrm{s}} + 0.6\,\frac{\mathrm{m}}{\mathrm{s}\cdot^\circ\mathrm{C}}T_C</math></center> | ||
| + | |||
| + | con <math>T_C</math> la temperatura en grados centígrados. Si un trombón debe tocar la misma nota de 440 Hz que el órgano y el trombón está a 25 ºC, pero el órgano se encuentra sólo a 15 ºC, ¿cuál es la frecuencia de los batidos que se escuchan? | ||
| + | |||
| + | ==[[Efecto Doppler de dos camiones en movimiento]]== | ||
| + | Dos camiones de bomberos acuden desde el este y el oeste a apagar un incendio situado entre ellos. Ambos camiones circulan a 80 km/h y hacen sonar sus sirenas a 600 Hz. Un viento de 50 km/h sopla del este al oeste. ¿Con qué frecuencia escucha las sirenas un observador situado en el punto intermedio? ¿Con qué frecuencia escucha cada conductor la sirena del otro camión? | ||
| + | |||
| + | [[Efecto Doppler de dos camiones en movimiento|'''Solución''']] | ||
| + | |||
| + | ==[[Efecto Doppler de dos vehículos]]== | ||
| + | Al lugar de un incendio acuden por la misma carretera rectilínea, en el mismo sentido, un coche de bomberos a 108 km/h y una ambulancia de 72 km/h. El coche de bomberos usa una sirena de 880 Hz, mientras que la ambulancia emplea una de 900 Hz. | ||
| + | |||
| + | # En un momento dado el coche de bomberos se encuentra a 4 km del lugar del incendio, y la ambulacia a 3.00 km de él y ambos vehículos hacen sonar sus sirenas. Para una persona situada en el camino de los vehículos, pero 1 km antes del lugar del incendio, ¿cuál de los dos sonidos emitidos en ese instante llega antes?, ¿qué sirena suena más aguda?, ¿en cuántos hercios? ¿Cuál es la frecuencia de la señal y de los batidos que oye esa persona? | ||
| + | # Para el conductor de la ambulancia y el del coche de bomberos, ¿cuál es la frecuencia que le llega del otro vehículo cuando se encuentran en la posición del apartado anterior? | ||
| + | # A los 2 minutos ambos vehículos hacen sonar sus sirenas otra vez. ¿cómo quedan los dos resultados de los dos apartados anteriores? | ||
| + | |||
| + | Supóngase la velocidad del sonido c = 340 m/s. | ||
| + | |||
| + | [[Efecto Doppler de dos vehículos|'''Solución''']] | ||
| + | |||
| + | ==[[Sonar de un murciélago]]== | ||
| + | Un murciélago que vuela hacia una pared emite un ultrasonido de frecuencia <math>f_0</math>. Recibe el eco un tiempo <math>\Delta t</math> más tarde y con una frecuencia <math>f_1</math>. Determine la velocidad con la que se mueve el murciélago y la distancia a la que se encuentra de la pared en el momento de recibir el eco. (Dato: ''c'' = 343 m/s) | ||
| + | |||
| + | ==Efecto Doppler aplicado al radar de un aeropuerto== | ||
| + | El radar de un aeropuerto emite señales con frecuencia <math>f_0</math>. Una de estas señales incide en un avión que se dirige hacia el aeropuerto. El radar recibe el eco un tiempo <math>\Delta t</math> después y con una frecuencia <math>f_1</math>. Determine la posición del avión en el momento en el que la torre de control recibe el eco. | ||
| + | |||
| + | ==[[Posición aparente de un avión]]== | ||
| + | Un observador escucha el ruido de un avión que se mueve con velocidad constante ''v'' (subsónica) a una altura ''h''. La trayectoria del avión pasa sobre la vertical del observador. Este torpe observador siempre mira en la dirección de la que viene el ruido. Para esta persona ¿cómo varía aparentemente la posición del avión con el tiempo? ¿Con qué velocidad se mueve aparentemente cuando se encuentra muy alejado acercándose? ¿Y cuando está muy lejos alejándose del observador? | ||
| + | |||
| + | ==[[Posición aparente de un avión supersónico]]== | ||
| + | Un avión supersónico vuela a Mach 1.8 a 3 km de altura. Determine el tiempo entre que pasa por la vertical de un observador situado en el suelo y que a éste le llegue el frente de la onda de choque. Cuando llega este sonido, ¿dónde parece que se encuentra el avión, a juzgar por el ruido? ¿A qué distancia de su posición real en ese instante? | ||
| + | |||
| + | ==[[Efecto Doppler de un tren que pasa frente al observador]]== | ||
| + | |||
| + | ==Cálculo de la intensidad límite audible== | ||
| + | La intensidad acústica más baja que puede percibir el oído a una frecuencia de 1 kHz es <math>I_0=10^{-12}\,\mathrm{W}/\mathrm{m}^2</math>. Calcule la amplitud del desplazamiento del tímpano y la sobrepresión en él en esa situación y para una intensidad | ||
| + | acústica de 120 dB, que corresponde al umbral de dolor. | ||
[[Categoría:Problemas de ondas sonoras|0]] | [[Categoría:Problemas de ondas sonoras|0]] | ||
[[Categoría:Problemas de Física Aeronáuticos|120]] | [[Categoría:Problemas de Física Aeronáuticos|120]] | ||
[[Categoría:Ondas sonoras]] | [[Categoría:Ondas sonoras]] | ||
última version al 21:02 26 mar 2010
1 Duración de un trueno
Un rayo cae desde una nube situada a 2 km de altura. Si el rayo cae verticalmente e impacta de forma casi instantánea en un punto situado a 10 km de un observador, ¿cuánto tarda un el trueno en llegar a este observador? ¿Cuánto dura este trueno? Suponga que el aire se encuentra a 20 ºC.
2 Onda sonora en agua
Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50 metros. El sistema emite un haz de ondas de sonido de frecuencia f = 262 Hz que forma un ángulo de 30º con la superficie del mar y mide el tiempo que tarda la onda, que se refleja en un pecio, en regresar al detector. Sabiendo que el tiempo de retardo es 0.135 segundos y que la densidad del agua es 1.06×10³ kg/m³, calcule
- La velocidad del sonido en el agua
- El módulo de compresibilidad del agua
- La longitud de onda de la señal emitida.
3 Tiempo de un sonido para llegar al suelo
La temperatura de la atmósfera en sus capas bajas decrece con la altura como

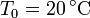
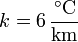
Un avión rompe la barrera del sonido cuando se encuentra a 8 km de altura. ¿Cuánto tarda el estampido sónico en llegar al suelo?
4 Batidos por diferencia de temperaturas
Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC. Admita que la velocidad del sonido en el aire a temperaturas próximas a la ambiente depende de la temperatura como
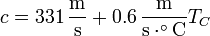
con TC la temperatura en grados centígrados. Si un trombón debe tocar la misma nota de 440 Hz que el órgano y el trombón está a 25 ºC, pero el órgano se encuentra sólo a 15 ºC, ¿cuál es la frecuencia de los batidos que se escuchan?
5 Efecto Doppler de dos camiones en movimiento
Dos camiones de bomberos acuden desde el este y el oeste a apagar un incendio situado entre ellos. Ambos camiones circulan a 80 km/h y hacen sonar sus sirenas a 600 Hz. Un viento de 50 km/h sopla del este al oeste. ¿Con qué frecuencia escucha las sirenas un observador situado en el punto intermedio? ¿Con qué frecuencia escucha cada conductor la sirena del otro camión?
6 Efecto Doppler de dos vehículos
Al lugar de un incendio acuden por la misma carretera rectilínea, en el mismo sentido, un coche de bomberos a 108 km/h y una ambulancia de 72 km/h. El coche de bomberos usa una sirena de 880 Hz, mientras que la ambulancia emplea una de 900 Hz.
- En un momento dado el coche de bomberos se encuentra a 4 km del lugar del incendio, y la ambulacia a 3.00 km de él y ambos vehículos hacen sonar sus sirenas. Para una persona situada en el camino de los vehículos, pero 1 km antes del lugar del incendio, ¿cuál de los dos sonidos emitidos en ese instante llega antes?, ¿qué sirena suena más aguda?, ¿en cuántos hercios? ¿Cuál es la frecuencia de la señal y de los batidos que oye esa persona?
- Para el conductor de la ambulancia y el del coche de bomberos, ¿cuál es la frecuencia que le llega del otro vehículo cuando se encuentran en la posición del apartado anterior?
- A los 2 minutos ambos vehículos hacen sonar sus sirenas otra vez. ¿cómo quedan los dos resultados de los dos apartados anteriores?
Supóngase la velocidad del sonido c = 340 m/s.
7 Sonar de un murciélago
Un murciélago que vuela hacia una pared emite un ultrasonido de frecuencia f0. Recibe el eco un tiempo Δt más tarde y con una frecuencia f1. Determine la velocidad con la que se mueve el murciélago y la distancia a la que se encuentra de la pared en el momento de recibir el eco. (Dato: c = 343 m/s)
8 Efecto Doppler aplicado al radar de un aeropuerto
El radar de un aeropuerto emite señales con frecuencia f0. Una de estas señales incide en un avión que se dirige hacia el aeropuerto. El radar recibe el eco un tiempo Δt después y con una frecuencia f1. Determine la posición del avión en el momento en el que la torre de control recibe el eco.
9 Posición aparente de un avión
Un observador escucha el ruido de un avión que se mueve con velocidad constante v (subsónica) a una altura h. La trayectoria del avión pasa sobre la vertical del observador. Este torpe observador siempre mira en la dirección de la que viene el ruido. Para esta persona ¿cómo varía aparentemente la posición del avión con el tiempo? ¿Con qué velocidad se mueve aparentemente cuando se encuentra muy alejado acercándose? ¿Y cuando está muy lejos alejándose del observador?
10 Posición aparente de un avión supersónico
Un avión supersónico vuela a Mach 1.8 a 3 km de altura. Determine el tiempo entre que pasa por la vertical de un observador situado en el suelo y que a éste le llegue el frente de la onda de choque. Cuando llega este sonido, ¿dónde parece que se encuentra el avión, a juzgar por el ruido? ¿A qué distancia de su posición real en ese instante?
11 Efecto Doppler de un tren que pasa frente al observador
12 Cálculo de la intensidad límite audible
La intensidad acústica más baja que puede percibir el oído a una frecuencia de 1 kHz es 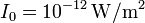 . Calcule la amplitud del desplazamiento del tímpano y la sobrepresión en él en esa situación y para una intensidad
acústica de 120 dB, que corresponde al umbral de dolor.
. Calcule la amplitud del desplazamiento del tímpano y la sobrepresión en él en esa situación y para una intensidad
acústica de 120 dB, que corresponde al umbral de dolor.





