Sonar de un murciélago
De Laplace
1 Enunciado
Un murciélago que vuela hacia una pared emite un ultrasonido de frecuencia f0. Recibe el eco un tiempo Δt más tarde y con una frecuencia f1. Determine la velocidad con la que se mueve el murciélago y la distancia a la que se encuentra de la pared en el momento de recibir el eco. (Dato: c = 343 m/s)
2 Solución
Vamos a calcular en primer lugar la velocidad del murciélago utlizando el corrimiento de frecuencias debido al efecto Doppler. El murciélago emite un sonido con frecuencia f0. Esta onda llega a la pared, donde rebota y es emitida hacia el murciélago con una frecuencia fp. Finalmente este sonido llega al murciélago con una frecuencia f1.
En el primer proceso la pared actúa como receptor y el murciélago como emisor. Así pues la frecuencia que percibe la pared es
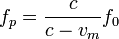
La velocidad vm se considera positiva pues el murciélago se acerca a la pared.
El sonido proveniente de la pared tiene frecuencia fp. Al llegar al murciélago, éste es el receptor y la pared es el emisor. Así pues la frecuencia que percibe el animal es
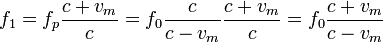
Despejando obtenemos la velocidad del murciélago en función de las frecuencias y la velocidad del sonido en el aire
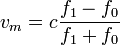
La velocidad del murciélago siempre será mucho menor que la del sonido en el aire. Entonces las frecuencias f0 y
f1 son muy parecidas. Se cumple por tanto, 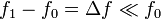 . Obtenemos así una
expresión más sencilla de la velocidad del murciélago
. Obtenemos así una
expresión más sencilla de la velocidad del murciélago
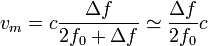
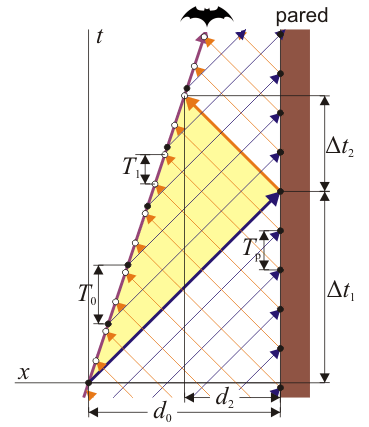
Vamos a calcular ahora la distancia a la que estaba el murciélago de la pared cuando emitió el sonido. Consideramos tres instantes de tiempo como se indica en la figura. En t = 0 el murciélago está a una distancia d0 de la pared y emite el ultrasonido. En t = Δt1 el ultrasonido llega a la pared y rebota. En ese momento el murciélago está a la distancia d1 de la pared. Finalmente, el ultrasonido emitido por la pared llega al murciélago en el instante Δt, estando el animal a la distancia d2 del muro.
Durante el tiempo Δt el murciélago ha seguido avanzando hacia la pared con velocidad vm. Por tanto, cuando recibe el ultrasonido la distancia d2 es
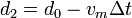
Tenemos que calcular d2. Para ello vemos que los intervalos de tiempo Δt1 y Δt2 valen
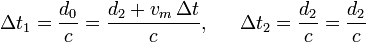
Sumando los dos tenemos
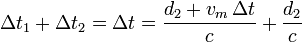
Despejando d2 queda
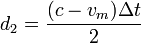
Observemos que si el murciélago no se mueve, tenemos vm = 0 y por tanto d2 = cΔt / 2.
Sustituyendo aquí vm, calculada anteriormente
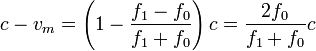

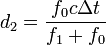
Si lo que tenemos es el corrimiento en la frecuencia y este es relativamente pequeño
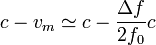

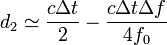
De nuevo podemos comprobar que si Δf = 0, se tiene d2 = cΔt / 2, como es lógico.
Los murciélagos se desplazan con velocidades alrededor de 5 m/s. Podemos estimar el desplazamiento de frecuencias que produce esta velocidad. De la expresión que nos da la velocidad del murciélago obtenemos

Si vm = 5 m/s y c = 343 m/s tenemos 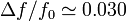 . Por tanto está justificado
utilizar las expresiones aproximadas.
. Por tanto está justificado
utilizar las expresiones aproximadas.