Test de la primera convocatoria de Física I 2014-2015 (GIE) (1ª parte)
De Laplace
Contenido |
1 Péndulo que desciende desde la horizontal
Un péndulo simple está formado por una masa m suspendida de un hilo de longitud b, sin masa, atado por su otro extremo de un punto fijo. Inicialmente se coloca el hilo extendido horizontalmente yse deja caer la masa desde el reposo.
1.1 Pregunta 1
¿Cuánto vale, en módulo, la tensión del hilo en el punto más bajo?
- A 2mg
- B 3mg
- C mg
- D 5mg
- Solución
La respuesta correcta es la B.
Este es un caso particular del problema Rapidez y tensión de un péndulo.
Por la segunda ley de Newton, en el punto más bajo se cumple
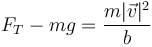
Por conservación de la energía mecánica, igualando la energía cinética en el punto más bajo con la potencial en el punto inicial (situado a una altura b respecto al más bajo):
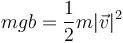
Despejando de aquí queda
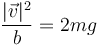
y sustituyendo en la primera

1.2 Pregunta 2
¿Qué trabajo total realiza la tensión del hilo en el trayecto desde la posición inicial hasta el punto más bajo?
- A 3mgb
- B mgb
- C − mgb
- D 0
- Solución
La respuesta correcta es la B.
La tensión no realiza trabajo porque en todo momento es perpendicular al desplazamiento y a la velocidad

2 Aceleración de dos partículas
Dos partículas, que cumplen m1 = 4m2 se encuentran inicialmente en reposo y a partir de ahí se mueven sometidas exclusivamente a fuerzas internas newtonianas. Sus aceleraciones cumplen que
- A
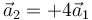
- B
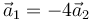
- C
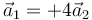
- D
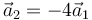
- A
- Solución
La respuesta correcta es la D.
Consecuencia inmediata de la tercera ley de Newton, como en otra pregunta ya conocida.
3 Caso de movimiento de un sólido
Un sólido se mueve de forma que el punto 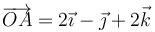 (m) tiene la velocidad
(m) tiene la velocidad 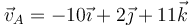 (m/s), siendo la velocidad angular del sólido
(m/s), siendo la velocidad angular del sólido 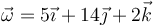 (rad/s)
(rad/s)
3.1 Pregunta 1
¿Qué tipo de movimiento está describiendo el sólido en ese instante?
- A Reposo.
- B Helicoidal.
- C Rotación.
- D Traslación.
- Solución
La respuesta correcta es la C.
No es reposo ni traslación por no ser nula la velocidad angular. Comprobamos si es ortogonal a la velocidad del punto
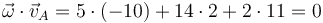
Como sí lo es, el movimiento es una rotación.
3.2 Pregunta 2
¿Cuál es, en ese instante, la velocidad del origen de coordenadas, O, en m/s?
- A
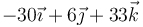
- B Nula.
- C 45.
- D
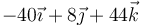
- A
- Solución
La respuesta correcta es la D.
Aplicación directa del teorema de Chasles
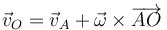
4 Movimiento de una masa por fuerza elástica
Una partícula de masa 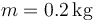 se encuentra unida al origen de coordenadas por un resorte elástico lineal, siendo la fuerza elástica la única que actúa sobre ella. Como resultado de la acción de esta fuerza, se mueve sobre una recta, con una elongación, en el SI,
se encuentra unida al origen de coordenadas por un resorte elástico lineal, siendo la fuerza elástica la única que actúa sobre ella. Como resultado de la acción de esta fuerza, se mueve sobre una recta, con una elongación, en el SI,
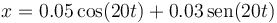
4.1 Pregunta 1
¿Cuánto vale la constante elástica del muelle?
- A No hay información suficiente para saberlo.
- B 0.5 mN/m
- C 4 N/m.
- D 80 N/m.
- Solución
La respuesta correcta es la D.
La frecuencia de la oscilación es
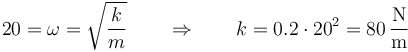
4.2 Pregunta 2
¿Cuánto vale la energía mecánica de esta partícula en cualquier instante t?
- A 36 mJ
- B (100+36cos(40t)) mJ
- C 136 mJ
- D 100 mJ
- Solución
La respuesta correcta es la C.
La energía mecánica es una constante de movimiento, siendo su valor el inicial
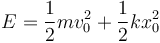
con
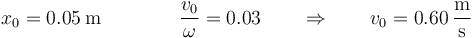
Sustituyendo queda
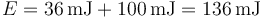
Alternativamente puede hallarse como
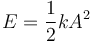
con
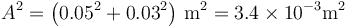
y k la hallada en la pregunta anterior.
5 Momento cinético de dos partículas
Un sistema está formado por dos partículas que en un instante dado se hallan situadas en el origen de coordenadas, O,. La primera tiene masa 40 g y velocidad 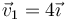 (m/s), la segunda tiene masa 20 g y velocidad
(m/s), la segunda tiene masa 20 g y velocidad 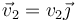 ¿Cuánto debe valer v2 para que el momento cinético del sistema respecto al punto B, de posición
¿Cuánto debe valer v2 para que el momento cinético del sistema respecto al punto B, de posición 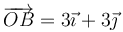 (m), sea nulo?
(m), sea nulo?
- A −8 m/s
- B Es imposible anular el momento cinético.
- C 8 m/s
- D 4 m/s
- Solución
La respuesta correcta es la C.
Debe anularse la cantidad
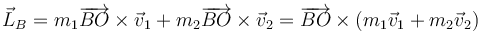
Para que se anule esta producto vectorial, la cantidad de movimiento
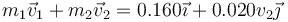
debe ser paralela al vector
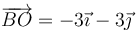
Lo cual ocurre si