Preguntas de test de dinámica de la partícula
De Laplace
Contenido |
1 Partícula que cuelga de dos muelles
Una partícula de peso 2 N cuelga del techo suspendida de dos muelles en paralelo, ambos de longitud natural 15 cm. El muelle 1 tiene constante 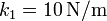 y el 2
y el 2 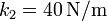 .
.
1.1 Pregunta 1
En el equilibrio, ¿cuál es la distancia de la partícula al techo?
- A 2 cm.
- B 75 cm.
- C 19 cm.
- D 40 cm.
- Solución
La respuesta correcta es la C.
El equilibrio se produce cuando el peso de la masa se compensa con la fuerza debida a los dos muelles, que actúan en el mismo sentido.
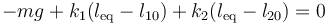
Puesto que los dos tienen la misma longitud natural, l0, esto se reduce a
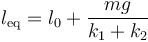
Sustituyendo los valores numéricos

1.2 Pregunta 2
Si, estando en la posición anterior, se corta la unión de la masa con el muelle 2, ¿cuánto vale la amplitud de las oscilaciones resultantes?
- A 1 cm.
- B 35 cm
- C 0 cm.
- D 16 cm.
- Solución
La respuesta correcta es la D.
Al cortar la unión al muelle 2, la masa empieza a oscilar alrededor de la posición de equilibrio del muelle 1, siendo la amplitud la diferencia entre la posición que ya tenía y la nueva posición de equilibrio.
Con solo el muelle 1, la nueva posición de equilibrio es
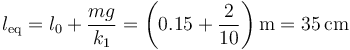
lo que da la amplitud

2 Masa que cuelga de dos hilos
Una partícula de peso 300 N cuelga de un techo horizontal sujeta por dos hilos (“1”' y “2”'). El hilo 1 forma un ángulo de 30° con la vertical, mientras que el hilo 2 forma uno de 60° con la vertical. ¿Cuánto valen, en módulo, las tensiones de los dos hilos?
- A
 ,
, 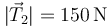
- B
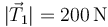 ,
, 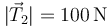
- C

- D
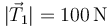 ,
, 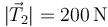
- Solución
La respuesta correcta es la A.
Al estar en equilibrio la masa se cumple
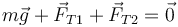
Separando en componentes cartesianas
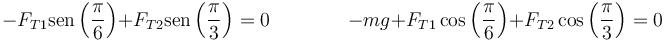
Sustituyendo las funciones trigonométricas obtenemos el sistema
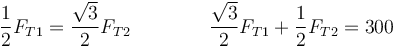
con solución
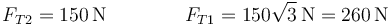
Hay que observar que, al no ser las dos tensiones vectores paralelos, la suma de sus módulos no puede ser igual al módulo del peso, por lo que las respuestas B, C y D no pueden ser correctas.
3 Fuerza entre dos cargas
Dos partículas cargadas con masas m1 = m y m2 = 2m y cargas q1 = q2 = q0 se encuentran a una cierta distancia la una de la otra. Se sujetan las dos partículas de forma que estén en reposo. Entonces se sueltan simultáneamente las dos. ¿Cómo son las dos aceleraciones de las partículas tras la liberación?
- A
 .
.
- B

- C
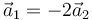 .
.
- D Nulas.
- Solución
La respuesta correcta es la C.
De acuerdo con la tercera ley de Newton
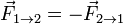
Aplicando aquí la segunda ley de Newton

Sustituimos los valores de las masas
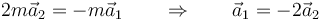
Se podía haber sacado observando que a igualdad de fuerza, cuanto mayor sea la masa (inercial) menor es la aceleración, por lo que la aceleración de la masa 2 debe ser menor en módulo que la de la masa 1.
4 Otra masa que cuelga de dos hilos
En la situación de equilibrio de la figura de una masa atada con dos hilos, ¿cuánto valen los módulos de las tensiones respectivas?
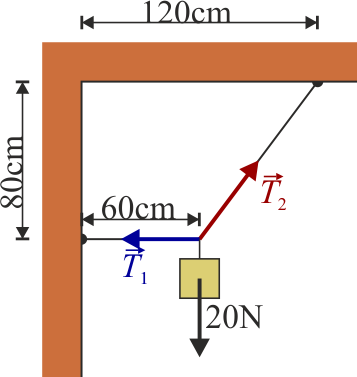
- A
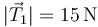 ,
, 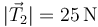 .
.
- B
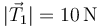 ,
, 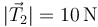 .
.
- C
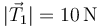 ,
, 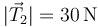 .
.
- D
 ,
, 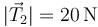 .
.
- Solución
La respuesta correcta es la A.
Esta pregunta se puede resolver separando en componentes como en una pregunta anterior.
Observamos que la única componente vertical la da el hilo que cuelga del techo, por lo que
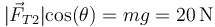
siendo la tangente del ángulo que forma con la vertical

y por tanto
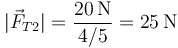
La componente horizontal de esta fuerza se cancela con la tensión del hilo horizontal
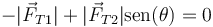
de donde
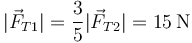
5 Movimiento de una partícula sometida a una fuerza constante
Una partícula de masa m se encuentra inicialmente en 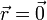 moviéndose con velocidad
moviéndose con velocidad
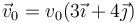 . Se encuentra sometida a una fuerza constante
. Se encuentra sometida a una fuerza constante 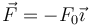
5.1 Pregunta 1
¿Qué tipo de trayectoria sigue la partícula?
- A Helicoidal
- B Rectilínea.
- C Parabólica
- D Elíptica
- Solución
La respuesta correcta es la C.
Al ser la fuerza constante, también lo es la aceleración

El movimiento de una partícula que tiene una aceleración constante es un movimiento parabólico. El caso paradigmático es el del tiro parabólico de un cuerpo sometido a la acción de la gravedad, pero la dirección de ésta no tiene mayor importancia. Cualquier fuerza constante producirá un afecto análogo y una trayectoria en forma de parábola.
Concretamente, la ecuación horaria es
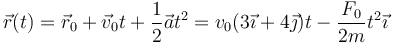
Separando por componentes
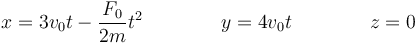
Si eliminamos el tiempo de esta ecuación queda la ecuación de una parábola.
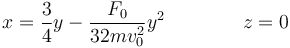
5.2 Pregunta 2
¿Cuánto vale su aceleración tangencial en t = 0?
- A Es nula.
- B − 3F0 / (5m).
- C 4F0 / (5m).
- D − 3F0 / m.
- Solución
La respuesta correcta es la B.
La aceleración tangencial la calculamos proyectando sobre la velocidad
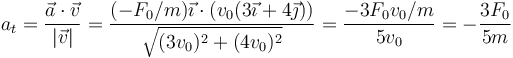
6 Comparación de fuerzas de rozamiento
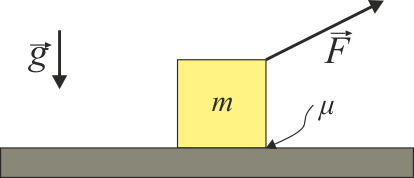
Se tienen las dos situaciones de las figuras.
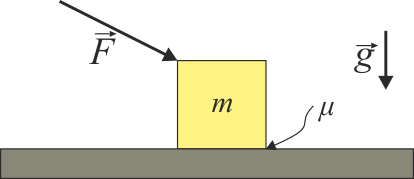
| 
|
| (a) | (b) |
En ambos casos el módulo de la fuerza aplicada y el ángulo con la horizontal es el mismo y el coeficiente de rozamiento estático es lo bastante grande como para que la masa no se mueva. ¿En cuál de las dos situaciones es mayor la fuerza de rozamiento?
- A En el caso (a)
- B En el caso (b)
- C Es la misma en los dos casos.
- D No hay forma de saberlo.
- Solución
La respuesta correcta es la C.
7 Péndulo en plano inclinado
Por un plano inclinado desciende sin rozamiento una caja rectangular. En el interior de la caja cuelga un péndulo que no está oscilando. Indique cuál de las siguientes figuras representa correctamente la inclinación del péndulo.

| 
|
| A | B |
|---|---|

| 
|
| C | D |
- Solución
La respuesta correcta es la A.
8 Péndulo rotatorio
En la ilustración de la figura una masa m está sujeta a un péndulo, pero gira sin oscilar. ¿Cuánto vale la velocidad angular con la que gira el soporte?
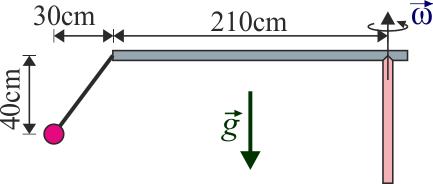
- A 4.20 rad/s
- B 1.75 rad/s.
- C 3.50 rad/s.
- D Depende del valor de la masa.
- Solución
La respuesta correcta es la B.
La masa describe un movimiento circular uniforme, por lo que su aceleración es puramente normal. Por tanto se cumple la segunda ley de Newton en la forma
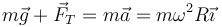
Tomando un sistema de ejes centrado en la masa en el que el eje OX es horizontal y hacia la derecha de la figura. El peso va en la dirección vertical
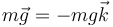
mientras que la tensión del hilo va a lo largo de éste
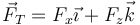
cumpliéndose
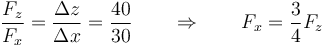
Despejamos de la segunda ley de Newton y queda,
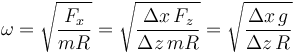
con el valor numérico