Rapidez y tensión de un péndulo

De Laplace

Contenido

1 Enunciado
2 Valor exacto
3 Valor aproximado
4 Comparación
5 Tensión
- 5.1 Punto inferior
- 5.2 Ángulo máximo

1 Enunciado

Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo simple de masa $m$ y longitud $l$ pasa por su punto más bajo, como función del ángulo máximo $θ 0$ con el que se separa de la vertical.

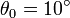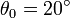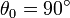
Compare este resultado con el que se obtiene empleando la aproximación lineal. Determine el error relativo cometido con esta aproximación para $\theta_0=10^\circ$ , $\theta_0=20^\circ$ ,… $\theta_0=90^\circ$

Determine la tensión de la cuerda en el punto más bajo y en el punto de máxima separación de la vertical. en función del ángulo $θ 0$

2 Valor exacto

La lenteja del péndulo está sometida a dos fuerzas: su peso y la tensión de la cuerda.

La tensión va siempre a lo largo de la propia cuerda y es por tanto perpendicular al desplazamiento en todo momento. Esto quiere decir que no realiza trabajo y no interviene en la ley de conservación de la energía.

La única energía potencial que debemos considerar es entonces la debida al peso. Tomando como origen de potencial el punto más bajo del péndulo, el valor de la energía potencial para una separación arbitraria $θ$ vale

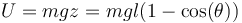
$U = mgz = mgl(1-\cos(\theta))\,$

Cuando consideramos oscilaciones del péndulo, el punto de máxima amplitud es uno de velocidad nula (alcanza un estado de reposo instantáneo a partir del cual se da la vuelta). Igualando la energía mecánica de este punto a la que tiene en elpunto mas bajo obtenemos la igualdad

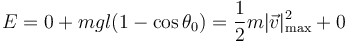
$E = 0 + mgl(1-\cos\theta_0)=\frac{1}{2}m |\vec{v}|_\mathrm{max}^2+ 0\,$

Obtenemos la velocidad máxima

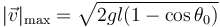
$|\vec{v}|_\mathrm{max} = \sqrt{2gl(1-\cos\theta_0)}$

Esta expresión se puede simplificar un poco observando que

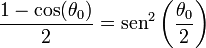
$\frac{1-\cos(\theta_0)}{2} = \mathrm{sen}^2\left(\frac{\theta_0}{2}\right)$

lo que da

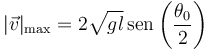
$|\vec{v}|_\mathrm{max} = 2\sqrt{gl}\,\mathrm{sen}\left(\frac{\theta_0}{2}\right)$

3 Valor aproximado

Un péndulo obedece la ecuación de movimiento

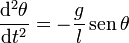
$\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\frac{g}{l}\,\mathrm{sen}\,\theta$

siendo $θ$ la inclinación respecto a la vertical (medida en radianes). Cuando esta separación es pequeña, se puede usar la aproximación lineal

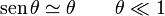
$\mathrm{sen}\,\theta\simeq\theta \qquad\theta\ll 1$

lo que reduce la ecuación del péndulo a la de un oscilador armónico

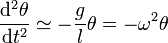
$\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}\simeq-\frac{g}{l}\theta=-\omega^2\theta$

Cuando parte del reposo, desde una cierta separación $θ 0$ , el ángulo sigue una ley cosenoidal

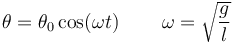
$\theta = \theta_0\cos(\omega t)\,\qquad\omega = \sqrt{\frac{g}{l}}$

La velocidad lineal de la lenteja del péndulo es

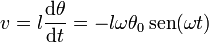
$v = l\frac{\mathrm{d}\theta}{\mathrm{d}t} = -l\omega\theta_0\,\mathrm{sen}(\omega t)$

El valor máximo (en módulo) de esta velocidad lo alcanza en el momento en que se encuentra en el punto más bajo

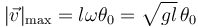
$|\vec{v}|_\mathrm{max}=l\omega\theta_0= \sqrt{gl}\,\theta_0$

4 Comparación

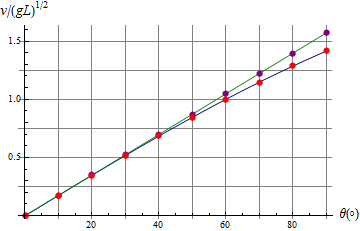
El cociente entre el valor aproximado y el exacto es

$\frac{|\vec{v}|_\mathrm{ap}}{|\vec{v}|_\mathrm{ex}} = \frac{\theta_0}{\sqrt{2(1-\cos\theta_0)}} = \frac{\theta_0/2}{\mathrm{sen}\,(\theta_0/2)}$

donde hemos empleado la fórmula del ángulo mitad. Dado que

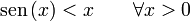
$\mathrm{sen}\,(x) < x\qquad \forall x > 0$

esto quiere decir que la aproximación de oscilador armónico predice una velocidad mayor que la real. El periodo calculado con esta aproximación será entonces más pequeño que el exacto.

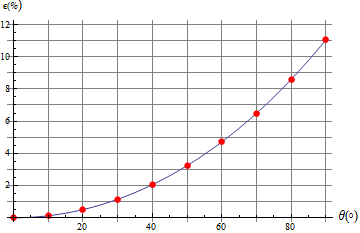
El error relativo cometido en la aproximación es

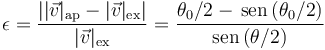
$\epsilon = \frac{\left||\vec{v}|_\mathrm{ap}-|\vec{v}|_\mathrm{ex}\right|}{|\vec{v}|_\mathrm{ex}} = \frac{\theta_0/2-\,\mathrm{sen}\,(\theta_0/2)}{\mathrm{sen}\,(\theta/2)}$

Aplicando esta fórmula a los ángulos del enunciado

$θ 0$ (°)	$θ 0$ (rad)	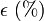$\epsilon\ (\%)$	$θ 0$ (°)	$θ 0$ (rad)	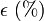$\epsilon\ (\%)$
10	0.1745	0.127	60	1.047	4.720
20	0.3491	0.510	70	1.222	6.501
30	0.5236	1.152	80	1.396	8.610
40	0.6981	2.060	90	1.571	11.07
50	0.8727	3.245

Vemos que, en general la aproximación es bastante buena y que incluso para ángulos tan grandes como 60° el error es inferior al 5 %.

5 Tensión

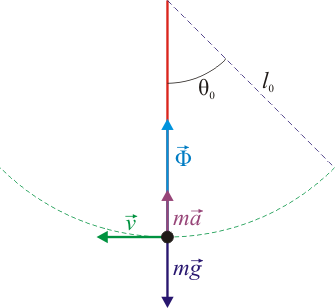
5.1 Punto inferior

En el punto más bajo las dos fuerzas son normales a la trayectoria y por tanto la aceleración tangencial es nula (por ello la rapidez tiene un máximo). La partícula, no obstante, está acelerada, pues posee aceleración normal. La segunda ley de Newton nos da

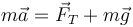
$m\vec{a} = \vec{F}_T+m\vec{g}$

siendo 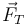$\vec{F}_T$ la fuerza de reacción vincular, en este caso, la tensión de la cuerda. Despejando de aquí

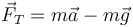
$\vec{F}_T = m\vec{a}-m\vec{g}$

El término debido al peso vale

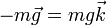
$-m\vec{g}=mg\vec{k}$

mientras que el debido a la aceleración normal es

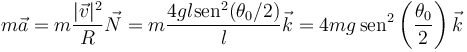
$m\vec{a}=m\frac{|\vec{v}|^2}{R}\vec{N} = m\frac{4gl\mathrm{sen}^2(\theta_0/2)}{l}\vec{k} = 4mg\,\mathrm{sen}^2\left(\frac{\theta_0}{2}\right)\vec{k}$

lo que nos da la tensión

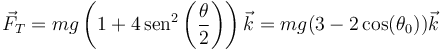
$\vec{F}_T= mg\left(1+4\,\mathrm{sen}^2\left(\frac{\theta}{2}\right)\right)\vec{k} = mg(3-2\cos(\theta_0))\vec{k}$

Esta tensión es siempre superior al peso. Sólo iguala al peso cuando la lenteja se encuentra en equilibrio en el punto inferior ( $θ 0 = 0$ ).

El valor máximo de la tensión se da para el caso que la partícula parta del extremo superior ( $θ 0 = π$ ), en cuyo caso iguala a 5 veces el peso. Este resultado es coincidente con el que se obtiene para una anilla ensartada en un aro, ya que el movimiento de dicha anilla es el mismo que el de un péndulo (la condición de vínculo es la misma: distancia constante al centro de la circunferencia).

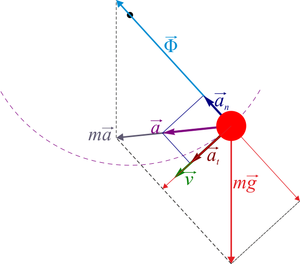
5.2 Ángulo máximo

En la posición de máxima separación de la vertical la aceleración normal es nula, por serlo la celeridad. No así la aceleración tangencial. Puesto que la fuerza de reacción vincular es puramente normal a la trayectoria tenemos las ecuaciones

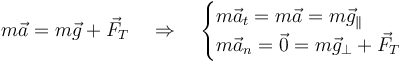
$m\vec{a}=m\vec{g}+\vec{F}_T\quad\Rightarrow\quad\begin{cases}m\vec{a}_t = m\vec{a} = m\vec{g}_\parallel & \\ m\vec{a}_n = \vec{0} = m\vec{g}_\perp + \vec{F}_T & \end{cases}$

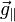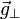siendo $\vec{g}_\parallel$ y $\vec{g}_\perp$ las componentes de la gravedad en la dirección tangente a la trayectoria y en la perpendicular a ella.

La tensión de la cuerda compensa entoces a la componente perpendicular de la gravedad

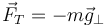
$\vec{F}_T=-m\vec{g}_\perp$

y, en módulo,

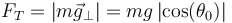
$F_T = |m\vec{g}_\perp|=mg\left|\cos(\theta_0)\right|$

En forma vectorial multiplicamos por el vector unitario en la dirección de la cuerda y hacia adentro

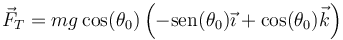
$\vec{F}_T=mg\cos(\theta_0)\left(-\mathrm{sen}(\theta_0)\vec{\imath}+\cos(\theta_0)\vec{k}\right)$

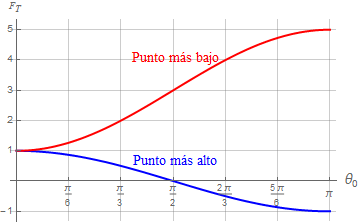
En módulo, esta tensión es siempre menor que el peso, salvo en el caso en que la partícula esté en equilibrio en el punto más bajo, en que se reduce al caso anterior.

La tensión se anula si la masa alcanza una posición horizontal ( $θ 0 = π / 2$ ). Para ángulos máximos superiores, la tensión debe ir dirigida hacia afuera lo que es posible si se trata de una barra rígida (vínculo bilateral), pero no si se trata de una cuerda flexible (vínculo unilateral). Para una barra rígida y un ángulo $θ 0 = π$ (extremo superior), la tensión vuelve a igualar al peso en módulo. Este caso está de nuevo de acuerdo con el sistema de una anilla ensartada en un aro.

Rapidez y tensión de un péndulo

De Laplace

Contenido

1 Enunciado

2 Valor exacto

3 Valor aproximado

4 Comparación

5 Tensión

5.1 Punto inferior

5.2 Ángulo máximo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES