Problemas de movimiento oscilatorio (CMR)

De Laplace

1 Tres masas unidas por resortes

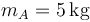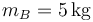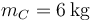Se tienen tres masas, de valores , y se hallan unidas por resortes. Entre la A y la B se encuentra uno de constante 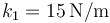y longitud natural 10cm, y entre la B y la C uno de constante 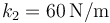y longitud natural 10cm. Inicialmente se encuentran las tres masas en reposo y los muelles en su longitud natural. Entonces se le comunica a la masa A una velocidad inicial .

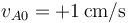Determine la posición de cada masa como función del tiempo.

Solución

2 Péndulo doble

Se tiene un péndulo doble plano. Está formado por una varilla rígida OA de masa despreciable y longitud 25 cm articulada en O y en cuyo extremo A se encuentra una masa de 1.6 kg. En A se halla articulada una segunda varilla AB, de masa también despreciable de la misma longitud 25 cm y en cuyo extremo B se encuentra una segunda masa de valor 0.9 kg. Tómese .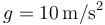

1. Determine las ecuaciones de movimiento para los ángulos φ, que forma OA con la vertical, y θ que forma AB con la prolongación de OA. Sugerencia: empléense los cálculos del problema “Dos barras articuladas”
2. Suponiendo que las dos varillas realizan oscilaciones muy próximas a la vetical, de manera que 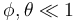, calcule las frecuencias de los modos normales de oscilación. ¿Cómo oscilan las varillas en cada uno de los modos normales.
3. Imaginemos que, estando las varillas en reposo, se sujeta la masa A y la varilla AB se coloca con una inclinación de 5º con respecto a la vertical. Entonces, se sueltan las dos masas. ¿Cómo es el movimiento posterior de cada una de ellas?

Solución