Tres masas unidas por resortes (CMR)
De Laplace
Contenido |
1 Enunciado
Se tienen tres masas, de valores 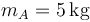 ,
, 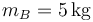 y
y 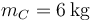 se hallan unidas por resortes. Entre la A y la B se encuentra uno de constante
se hallan unidas por resortes. Entre la A y la B se encuentra uno de constante 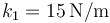 y longitud natural 10cm, y entre la B y la C uno de constante
y longitud natural 10cm, y entre la B y la C uno de constante 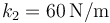 y longitud natural 10cm. Inicialmente se encuentran las tres masas en reposo y los muelles en su longitud natural. Entonces se le comunica a la masa A una velocidad inicial
y longitud natural 10cm. Inicialmente se encuentran las tres masas en reposo y los muelles en su longitud natural. Entonces se le comunica a la masa A una velocidad inicial 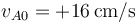 .
.
Determine la posición de cada masa como función del tiempo.
2 Ecuaciones de movimiento
En lo que sigue se usarán todas las magnitudes en las unidades fundamentales del SI.
Dado un sistema de referencia fijo, las posiciones de las tres partículas serán, respectivamente XA(t), XB(t) y XC(t). Por comodidad, definimos las variables
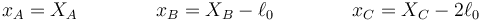
siendo 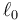 la longitud natural de ambos resortes. De esta manera podemos describir el movimiento como las desviaciones respecto a posiciones de equlibrio y podemos tratar los resortes como si tuvieran longitud natural nula.
la longitud natural de ambos resortes. De esta manera podemos describir el movimiento como las desviaciones respecto a posiciones de equlibrio y podemos tratar los resortes como si tuvieran longitud natural nula.
Las ecuaciones de movimiento las da la segunda ley de Newton. Para la primera masa
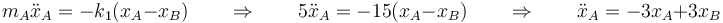
Para la segunda
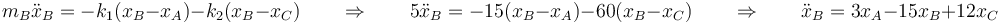
y para la tercera
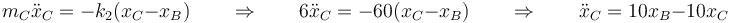
Por tanto, el sistema de ecuaciones de movimiento es
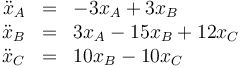
con las condiciones iniciales
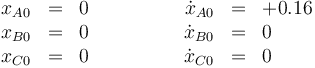
3 Modos normales
El sistema de ecuaciones de movimiento puede escribirse en forma matricial como
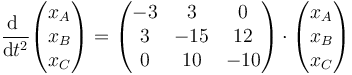
Existen diferentes formas de resolver este sistema de ecuaciones diferenciales de coeficientes constantes.
Una de ellas consiste en buscar los llamados modos normales, que son oscilaciones del sistema con una frecuencia completa, de forma que la solución puede escribirse en la forma
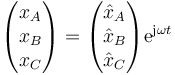
Una solución de este tipo no cumplirá, en general, las condiciones iniciales. Sin embargo, puede demostrarse que la solución general es una combinación lineal de los diferentes modos normales. El problema se traslada entonces a encontrar los coeficientes adecuados para cada caso concreto.
Veamos primero cuáles son los modos normales en este caso. Sustituyendo la solución propuesta la ecuación diferencial se transforma en la ecuación algebraica

o, agrupando términos,
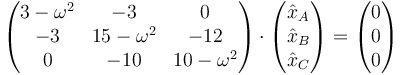
Este sistema es homogéneo. Para que haya soluciones distinta de l trivial (0,0,0) debe cumplirse que el determinante de la matriz de coeficientes se anule, en cuyo caso resulta un sistema indeterminado. Es decir, los valores de ω posibles vienen dados por la ,
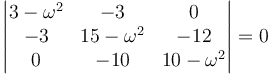
Desarrollamos el determinante y resulta la ecuación
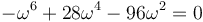
Vemos que resulta una ecuación de sexto grado, por lo que hay 6 posibles modos normales. Una ecuación de sexto grado no tiene solución general, pero en este caso podemos obser var que en realidad se trata de una ecuación cúbica en ω2, que sí la tiene. Es más, en este caso podemos sacar factor común y escribirla como
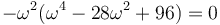
con lo que problema se reduce a resolver una ecuación se segundo grado en ω². Esto nos da las soluciones para ω²
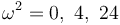
y para ω
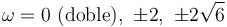
Dejaremos el caso de la solución ω = 0 para el final y consideraremos antes el resto de casos.
3.1 Caso ω² = 4
Una vez que tenemos la frecuencia debemos buscar la forma de las amplitudes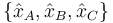
En el caso ω² = 4, la ecuación se convierte en
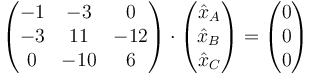
lo que nos da las ecuaciones
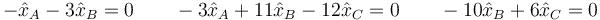
Estas ecuaciones no son las tres independientes, al ser nulo el determinante. Podemos determinar dos variables en función de la tercera. Por ejemplo

Dada una solución, cualquier múltiplo de ella es también solución. Podemos elegir arbitrariamente 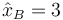 y tener la solución
y tener la solución
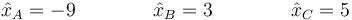
Por tanto, los dos primeros modos normales son

3.2 Caso ω² = 24
En el segundo caso, operamos de manera análoga. Sustituyendo ω² = 24 resulta la ecuación
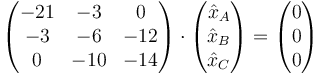
cuyas soluciones son los múltiplos de
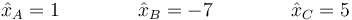
Por tnto, los siguientes dos modos normales son de la forma

En realidad, tanto en este caso como en el anterior, las dos soluciones corresponden al mismo modo de oscilación, entendido como forma en la que se mueven las partículas.
3.3 Caso ω² = 0
El caso ω² = 0 es un poco especial ya que no se trata de una solución oscilante. Si la frecuencia es nula, lo que se cumple en realidad es que
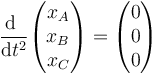
y si la segunda derivada es nula, eso quiere decir que cada variable esde la forma x = A + Bt, es decir corresponde a un movimiento uniforme. No obstante, las tres variables no son independientes, ya que deben seguir cumpliendo el sistema de ecuaciones
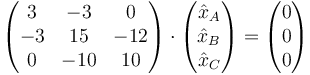
cuya solución es simplemente
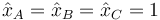
Por tanto, las dos últimas soluciones independientes son de la forma

El significado físico de estas dos soluciones es sencillo.
La primera corresponde a que estando las tres masas a las distancias de equiibrio las desplazamos una cierta cantidad fija e igual para las tres. El sistema sigue estando en equilibrio.
La segunda corresponde a un movimiento uniforme en que las tres masas se desplazan con la misma velocidad, manteniendo las distancias respectivas.
4 Solución particular
Una vez que tenemos las 6 soluciones independientes, la solución general es de la forma
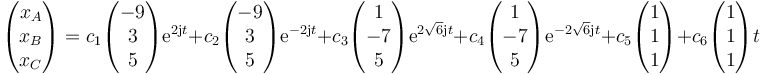
Siendo las velocidades
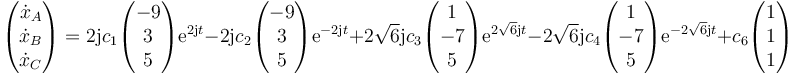
Para hallar los coeficientes imponemos las condiciones iniciales. Hacemos t = 0 y queda
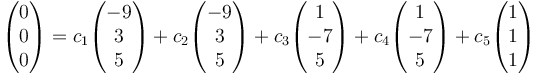
y
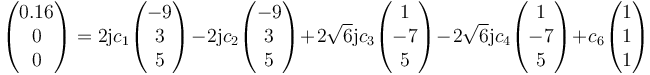
Esto nos da el sistema de ecuaciones
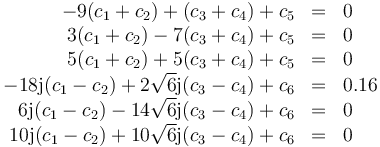
Con solución
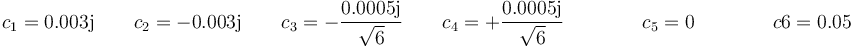
Llevando esto a la expresión general queda
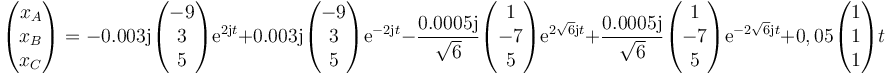
Aplicando aquí la fórmula de Euler
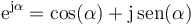
resulta
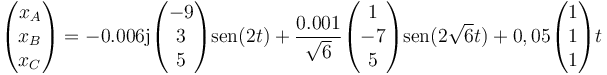
o separando por componentes
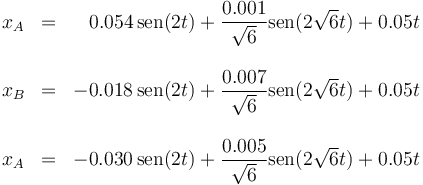
5 Solución en el sistema centro de masas
Una forma alternativa de abordar este problema consiste en identificar en primer lugar el movimiento del CM y a continuación analizar como se mueven las masas respecto al CM.
Por ser todas las fuerzas internas, el movimiento del CM es rectilíneo y uniforme, siendo su posición y velocidad inicial

(posteriormente a xG habría que sumarle 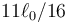 , que es su posición teniendo en cuenta las longitudes de los muelles)
Si ahora definimos coordenadas de cada masa respecto al CM
, que es su posición teniendo en cuenta las longitudes de los muelles)
Si ahora definimos coordenadas de cada masa respecto al CM
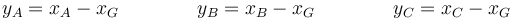
Estas tres coordenadas cumplen el vínculo

Las ecuaciones diferenciales para las y's son las mismas para las x's
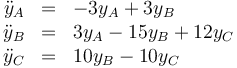
pero sustituyendo la ecuación de vínculo se puede reducir a solo dos
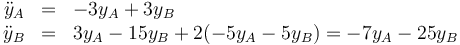
Con esto reduce el análisis a una matriz 2×2 y una ecuación de segundo grado en ω². El resultado final es, lógicamente, el mismo que antes.





