Péndulo doble (CMR)

De Laplace

Contenido

1 Enunciado
2 Ecuaciones de movimiento
3 Aproximación para ángulos pequeños
- 3.1 Sistema de ecuaciones
- 3.2 Modos normales
4 Solución particular

1 Enunciado

Se tiene un péndulo doble plano. Está formado por una varilla rígida OA de masa despreciable y longitud 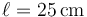$\ell=25\,\mathrm{cm}$ articulada en O y en cuyo extremo A se encuentra una masa 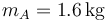$m_A=1.6\,\mathrm{kg}$ . En A se halla articulada una segunda varilla AB, de masa también despreciable, de la misma longitud math>\ell=25\,\mathrm{cm}</math> y en cuyo extremo B se encuentra una segunda masa de valor 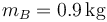$m_B=0.9\,\mathrm{kg}$ . 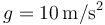Tómese $g = 10\,\mathrm{m}/\mathrm{s}^2$ .

Determine las ecuaciones de movimiento para los ángulos $φ$ , queg forma OA con la vertical, y θ que forma AB con la prolongación de OA. Sugerencia: empléense los cálculos del problema “Dos barras articuladas”
Suponiendo que las dos varillas realizan oscilaciones muy próximas a la vetical, de manera que 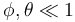$\phi,\theta\ll 1$ , calcule las frecuencias de los modos normales de oscilación. ¿Cómo oscilan las varillas en cada uno de los modos normales.
Imaginemos que, estando las varillas en reposo, se sujeta la masa A con OA vertical. La varilla AB se coloca con una inclinación de 10º con respecto a la vertical. Entonces, se sueltan las dos masas. ¿Cómo es el movimiento posterior de cada una de ellas?

2 Ecuaciones de movimiento

2.1 Para la masa A

Siguiendo los cálculos y la notación del problema “Dos barras articuladas” la segunda ley de Newton para la partícula A es

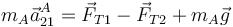
$m_A \vec{a}^A_{21}=\vec{F}_{T1}-\vec{F}_{T2}+m_A\vec{g}$

siendo 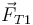$\vec{F}_{T1}$ la tensión de la varilla OA, que va dirigida a lo largo de la propia varilla

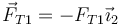
$\vec{F}_{T1}=-F_{T1}\vec{\imath}_2$

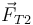$\vec{F}_{T2}$ la tensión de la varilla AB. En el extremo B tira hacia a A y en el extremo A tira hacia B.

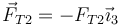
$\vec{F}_{T2}=-F_{T2}\vec{\imath}_3$

Por su parte, el peso va en la dirección del eje OX positivo

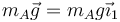
$m_A\vec{g}=m_A g\vec{\imath}_1$

La aceleración de A, tal como se ve en el problema mencionado, es

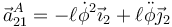
$\vec{a}^A_{21}=-\ell\dot{\phi}^2\vec{\imath}_2+\ell\ddot{\phi}\vec{\jmath}_2$

Todo esto nos da la ecuación

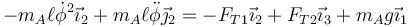
$-m_A\ell\dot{\phi}^2\vec{\imath}_2+m_A\ell\ddot{\phi}\vec{\jmath}_2=-F_{T1}\vec{\imath}_2+F_{T2}\vec{\imath}_3+m_Ag\vec{\imath}_1$

2.2 Para la masa B

La segunda ley de Newton en este caso es

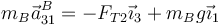
$m_B \vec{a}^B_{31}=-F_{T2}\vec{\imath}_3+m_Bg\vec{\imath}_1$

siendo la aceleración de B

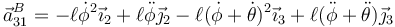
$\vec{a}^B_{31}=-\ell\dot{\phi}^2\vec{\imath}_2+\ell\ddot{\phi}\vec{\jmath}_2-\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3$

lo que nos da la ecuación de movimiento

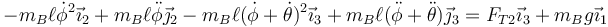
$-m_B\ell\dot{\phi}^2\vec{\imath}_2+m_B\ell\ddot{\phi}\vec{\jmath}_2-m_B\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+m_B\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3=F_{T2}\vec{\imath}_3+m_Bg\vec{\imath}_1$

2.3 Para los ángulos

En las ecuaciones anteriores podemos eliminar las tensiones, que son cantidades desconocidas, proyectando en las direcciones ortogonales. Así, en la ecuación de movimiento para B multiplicamos escalarmente por 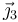$\vec{\jmath}_3$ y resulta

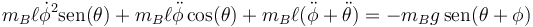
$m_B\ell\dot{\phi}^2\mathrm{sen}(\theta)+m_B\ell\ddot{\phi}\cos(\theta)+m_B\ell(\ddot{\phi}+\ddot{\theta})=-m_Bg\,\mathrm{sen}(\theta+\phi)$

Los productos escalares entre los vectores de las diferentes bases se deducen en el problema de cinemática ya citado.

Para eliminar la tensión de la varilla OA primero sumamos las dos ecuaciones de movimiento. De esta forma se elimina la tensión de la varilla AB, que es una fuerza interna, y queda

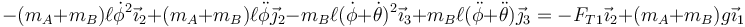
$-(m_A+m_B)\ell\dot{\phi}^2\vec{\imath}_2+(m_A+m_B)\ell\ddot{\phi}\vec{\jmath}_2-m_B\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+m_B\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3=-F_{T1}\vec{\imath}_2+(m_A+m_B)g\vec{\imath}_1$

Si aquí multiplicamos escalarmente por 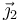$\vec{\jmath}_2$ resulta

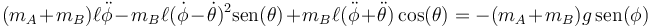
$(m_A+m_B)\ell\ddot{\phi}-m_B\ell(\dot{\phi}-\dot{\theta})^2\mathrm{sen}(\theta)+m_B\ell(\ddot{\phi}+\ddot{\theta})\cos(\theta)=-(m_A+m_B)g\,\mathrm{sen}(\phi)$

Podemos escribir estas ecuaciones de una manera menos engorrosa definiendo los parámetros

$\Omega=\sqrt{\frac{g}{\ell}}\qquad\qquad \gamma = \frac{m_B}{m_A}$

y resulta el sistema

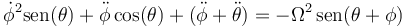
$\dot{\phi}^2\mathrm{sen}(\theta)+\ddot{\phi}\cos(\theta)+(\ddot{\phi}+\ddot{\theta})=-\Omega^2\,\mathrm{sen}(\theta+\phi)$

y

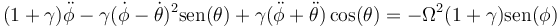
$(1+\gamma)\ddot{\phi}-\gamma(\dot{\phi}-\dot{\theta})^2\mathrm{sen}(\theta)+\gamma(\ddot{\phi}+\ddot{\theta})\cos(\theta)=-\Omega^2(1+\gamma) \mathrm{sen}(\phi)$

3 Aproximación para ángulos pequeños

3.1 Sistema de ecuaciones

El sistema de ecuaciones general para cualquier valor de los ángulos y las masas no posee solución analítica y es preciso recurrir a métodos numéricos para obtener la solución en casos particulares.

Si los ángulos de desviación respecto a la vertical son pequeños, podemos hacer la llamada aproximación lineal, en la cual se desprecian las potencias de grado superior al primero.

En la misma aproximación

$\mathrm{sen}(\alpha)\simeq \alpha\qquad\qquad \cos(\alpha)\simeq 1$

En ese caso, la primera de las dos ecuaciones se aproxima por

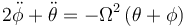
$2\ddot{\phi}+\ddot{\theta}=-\Omega^2\,(\theta+\phi)$

y la segunda

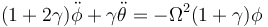
$(1+2\gamma)\ddot{\phi}+\gamma\ddot{\theta}=-\Omega^2(1+\gamma) \phi$

En estas ecuaciones podemos despejar las aceleraciones angulares y queda

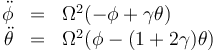
$\begin{array}{rcl} \ddot{\phi}&=&\Omega^2 (-\phi+\gamma\theta)\\ \ddot{\theta}&=&\Omega^2(\phi-(1+2\gamma)\theta) \end{array}$

o, en forma matricial,

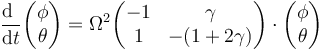
$\frac{\mathrm{d}\ }{\mathrm{d}t}\begin{pmatrix}\phi\\ \theta\end{pmatrix}=\Omega^2 \begin{pmatrix} -1 & \gamma \\ 1 & -(1+2\gamma)\end{pmatrix}\cdot\begin{pmatrix}\phi\\ \theta\end{pmatrix}$

3.2 Modos normales

Este es un sistema de ecuaciones que se puede resolver mediante la búsqueda de sus modos normales. Se trata de buscar soluciones exponenciales

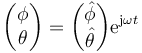
$\begin{pmatrix}\phi\\ \theta\end{pmatrix} = \begin{pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega t}$

La solución general es una combinación lineal de todos los modos normales posibles.

Sustituyendo esta solución en el sistema de ecuaciones diferenciales queda la ecuación algebraica

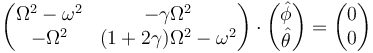
$\begin{pmatrix} \Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}$

Para que este sistema tenga solución no trivial debe anularse el determinante

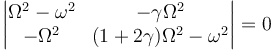
$\left|\begin{matrix} \Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{matrix}\right|=0$

Esto nos da la ecuación de cuarto grado

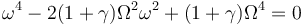
$\omega^4 -2(1+\gamma)\Omega^2\omega^2+(1+\gamma)\Omega^4 = 0\,$

Esta ecuación es, en realidad, una ecuación de segundo frado en ω², con soluciones

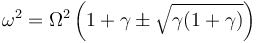
$\omega^2 = \Omega^2 \left(1+\gamma\pm\sqrt{\gamma(1+\gamma)}\right)$

Se puede hallar una solución general, para cualquier valor de Ω y γ. Sin embargo, ello implica el uso de numerosas raíces cuadradas. Por ello, aquí sustituiremos los valores numéricos del problema, que no son casuales, sino elegidos para que resulte una solución simple.

Empleando las unidades fundamentales del sistema internacional (kg,m y s)

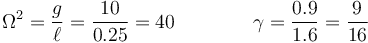
$\Omega^2 = \frac{g}{\ell}=\frac{10}{0.25}=40\qquad\qquad \gamma = \frac{0.9}{1.6}=\frac{9}{16}$

lo que nos da las frecuencias

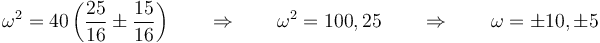
$\omega^2=40\left(\frac{25}{16}\pm\frac{15}{16}\right)\qquad\Rightarrow\qquad \omega^2 = 100,25\qquad\Rightarrow\qquad \omega = \pm 10,\pm 5$

3.2.1 Caso ω²=100

Las amplitudes de la oscilación son las soluciones de la ecuación

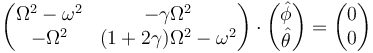
$\begin{pmatrix} \Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}$

Sustituímos los valores numéricos

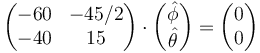
$\begin{pmatrix} -60 & -45/2\\ -40 & 15\end{pmatrix}\cdot\begin{pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}$

Esta ecuación tiene infinitas soluciones, ya que el sistema es indeterminado. Una de ellas es

$\hat{\phi}=-3\qquad\qquad \hat{\theta}=8$

Por tanto, las dos primeras soluciones de la ecuación diferencial son

$\begin{pmatrix}\phi\\ \theta\end{pmatrix} = \begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{10\mathrm{j}t}\qquad\qquad \begin{pmatrix}\phi\\ \theta\end{pmatrix} = \begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{-10\mathrm{j}t}$

3.2.2 Caso ω²=25

Sustituímos los valores numéricos

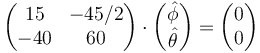
$\begin{pmatrix} 15 & -45/2\\ -40 & 60\end{pmatrix}\cdot\begin{pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}$

Una de las infinitas soluciones es

$\hat{\phi}=3\qquad\qquad \hat{\theta}=2$

Por tanto, la tercera y cuarta soluciones de la ecuación diferencial son

$\begin{pmatrix}\phi\\ \theta\end{pmatrix} = \begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{5\mathrm{j}t}\qquad\qquad \begin{pmatrix}\phi\\ \theta\end{pmatrix} = \begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{-5\mathrm{j}t}$

3.2.3 Solución general

Combinando las dos soluciones anteriores queda la solución general

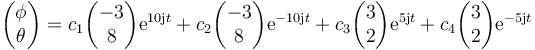
$\begin{pmatrix}\phi\\ \theta\end{pmatrix} = c_1 \begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{10\mathrm{j}t}+c_2\begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{-10\mathrm{j}t}+c_3\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{5\mathrm{j}t}+c_4\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{-5\mathrm{j}t}$

siendo sus derivadas respecyo al tiempo

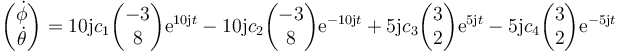
$\begin{pmatrix}\dot{\phi}\\ \dot{\theta}\end{pmatrix} = 10\mathrm{j}c_1 \begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{10\mathrm{j}t}-10\mathrm{j}c_2\begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{-10\mathrm{j}t}+5\mathrm{j}c_3\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{5\mathrm{j}t}-5\mathrm{j}c_4\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{-5\mathrm{j}t}$

4 Solución particular

Como caso particular nos dan las condiciones iniciales

$\phi_0=0\qquad\qquad \theta_0=10^\circ\qquad\qquad \dot{\phi}_0=0\qquad\qquad \dot{\theta}_0=0$

Imponemos estas condiciones haciendo t = 0 en la solución general. Queda

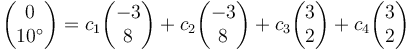
$\begin{pmatrix}0\\ 10^\circ\end{pmatrix} = c_1 \begin{pmatrix}-3\\ 8\end{pmatrix}+c_2\begin{pmatrix}-3\\ 8\end{pmatrix}+c_3\begin{pmatrix}3\\ 2\end{pmatrix}+c_4\begin{pmatrix}3\\ 2\end{pmatrix}$

y

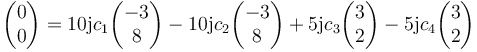
$\begin{pmatrix}0\\ 0\end{pmatrix} = 10\mathrm{j}c_1 \begin{pmatrix}-3\\ 8\end{pmatrix}-10\mathrm{j}c_2\begin{pmatrix}-3\\ 8\end{pmatrix}+5\mathrm{j}c_3\begin{pmatrix}3\\ 2\end{pmatrix}-5\mathrm{j}c_4\begin{pmatrix}3\\ 2\end{pmatrix}$

Desarrollando el sistema y resolviendo para los coeficientes queda

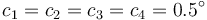
$c_1=c_2=c_3=c_4=0.5^\circ\,$

Por tano, la solución dependiente del tiempo es

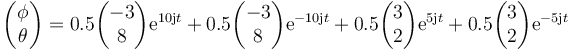
$\begin{pmatrix}\phi\\ \theta\end{pmatrix} = 0.5 \begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{10\mathrm{j}t}+0.5\begin{pmatrix}-3\\ 8\end{pmatrix}\mathrm{e}^{-10\mathrm{j}t}+0.5\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{5\mathrm{j}t}+0.5\begin{pmatrix}3\\ 2\end{pmatrix}\mathrm{e}^{-5\mathrm{j}t}$

Si igualamos componente a componente y aplicamos la fórmula de Euler queda, finalmente

$\phi=-3 \cos(10t)+3\cos(5t)\qquad\qquad \theta=8\cos(10t)+2\cos(10t)$

Péndulo doble (CMR)

De Laplace

Contenido

1 Enunciado

2 Ecuaciones de movimiento

2.1 Para la masa A

2.2 Para la masa B

2.3 Para los ángulos

3 Aproximación para ángulos pequeños

3.1 Sistema de ecuaciones

3.2 Modos normales

3.2.1 Caso ω²=100

3.2.2 Caso ω²=25

3.2.3 Solución general

4 Solución particular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES