Problemas de dinámica vectorial (CMR)
De Laplace
1 Oscilador armónico en el plano
Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico
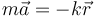 con
con 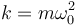 y
y 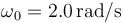 . Su posición inicial es
. Su posición inicial es 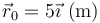
- Para el caso
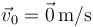 . ¿Qué tipo de movimiento describe la partícula?
. ¿Qué tipo de movimiento describe la partícula?
- Para el caso
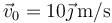 , ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
- Suponga ahora que
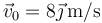 , ¿cómo es ahora la trayectoria de la partícula? ¿Cuál es la mínima distancia del origen a la que pasa la partícula?
, ¿cómo es ahora la trayectoria de la partícula? ¿Cuál es la mínima distancia del origen a la que pasa la partícula?
- Demuestre que en todos los casos la cantidad calculada en coordenadas polares
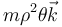 es constante.
es constante.
2 Péndulo simple
Un péndulo simple está formado por una masa m unida a una varilla rígida de longitud 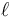 , unida por su otro extremo a un punto fijo O mediante una articulación esférica. La masa está sometida a la acción del peso.
, unida por su otro extremo a un punto fijo O mediante una articulación esférica. La masa está sometida a la acción del peso.
- Considere, en primer lugar, el movimiento en un plano vertical. Determine la ecuación de movimiento para el ángulo θ que la varilla forma con la vertical. ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
- Considere el caso de un péndulo cónico, el cual gira con velocidad angular constante
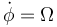 alrededor del eje vertical. ¿Cuál debe ser la relación entre Ω y el ángulo con la vertical, θ, para que este movimiento sea posible? ¿Puede conseguirse un movimiento circular sea cual sea Ω?
alrededor del eje vertical. ¿Cuál debe ser la relación entre Ω y el ángulo con la vertical, θ, para que este movimiento sea posible? ¿Puede conseguirse un movimiento circular sea cual sea Ω?
- Suponga ahora el movimiento general, en el cual puede cambiar tanto θ como el ángulo
 , de giro alrededor del eje vertical. A partir de la 2ª ley de Newton, obtenga las ecuaciones de movimiento para estos dos ángulos. Esto puede hacerse de diferentes maneras:
, de giro alrededor del eje vertical. A partir de la 2ª ley de Newton, obtenga las ecuaciones de movimiento para estos dos ángulos. Esto puede hacerse de diferentes maneras:
- Empleando coordenadas esféricas.
- Empleando un sistema de referencia en rotación alrededor del eje vertical, y empleando las fuerzas ficticias necesarias.
- Considerando una composición de movimientos mediante tres sistemas de referencia: uno fijo “1”, uno intermedio “2” que gira alrededor del eje vertical un ángulo φ y uno ligado “3” que gira respecto a un eje horizontal un ángulo θ.
- Considerando el caso general, con movimiento en las dos coordenadas
 y θ, suponga que con un motor se fuerza a una rotación constante
y θ, suponga que con un motor se fuerza a una rotación constante 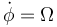 . En ese caso, ¿cómo queda la ecuación para θ? ¿Qué puntos de equilibrio hay? ¿Son estables o inestables?
. En ese caso, ¿cómo queda la ecuación para θ? ¿Qué puntos de equilibrio hay? ¿Son estables o inestables?
3 Alambre parabólico
Una pequeña anilla de masa m está ensartada en un alambre de forma parabólica, situado en un plano vertical. Esta parábola tiene su vértice en O(0,0,0) y cuando la partícula se halla a una distancia b del eje, su altura es (b / 2), con b fijado. Este alambre parabólico se hace girar alrededor del eje con velocidad angular constante Ω. No hay rozamiento entre la anilla y el alambre
- Escriba las ecuaciones de vínculo para la posición de la anilla, en coordenadas cartesianas y en coordenadas cilíndricas. ¿De qué clase de vínculos se trata?
- Escriba las ecuaciones de vínculo en forma cinemática y en forma pfaffiana.
- Escriba las ecuaciones de movimiento para esta partícula, en cartesianas y en polares, incluyendo las fuerzas de reacción vincular necesarias.
4 Rodadura de una esfera
Una esfera de radio R rueda y pivota sin deslizar sobre una superficie horizontal z = − R. las coordenadas del centro de la esfera G(x,y,0) están vinculadas a la rotación de la bola por la condición de no deslizamiento.
- Suponiendo una velocidad angular genérica
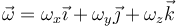 , escriba los vínculos cinemático entre la velocidad de G y la angular.
, escriba los vínculos cinemático entre la velocidad de G y la angular.
- Si la velocidad angular se escribe en términos de los ángulos de Euler, ¿cómo quedan los vínculos entre las coordenadas
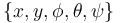 ?
?
- Si la velocidad angular se escribe en términos de los ángulos de Tait-Bryan, ¿cómo quedan los vínculos entre las coordenadas
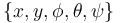 ?
?
5 Partícula en cono
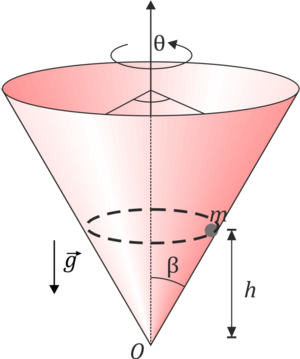
Una partícula está obligada a moverse por la superficie interior de un cono que tiene su vértice en el origen y que tiene un semiángulo de apertura β, es decir, la superficie del cono es, en cilíndricas z = ρ / tg(β). La partícula se mueve sin rozamiento por esta superficie y se halla sometida a la acción de la gravedad, que va en la dirección y sentido del eje OZ negativo
- Obtenga las ecuaciones de movimiento para esta partícula, empleando como coordenadas las cilíndricas, introduciendo las fuerzas de reacción oportunas.
- Reduzca este sistema a dos ecuaciones, una para la distancia al vértice,
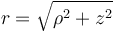 y otra para el ángulo θ, de manera que no aparezcan ρ, z ni la tensión.
y otra para el ángulo θ, de manera que no aparezcan ρ, z ni la tensión.
- ¿A qué velocidad debe moverse la partícula si se desea que describa un movimiento circular horizontal, a una altura H respecto al vértice? ¿Cuánto vale la fuerza de reacción en ese caso?
- Supongamos que parte de una altura H con una velocidad horizontal menor que la del apartado anterior. ¿Cuánto vale la mínima altura a la que llega la partícula?
6 Doble máquina de Atwood
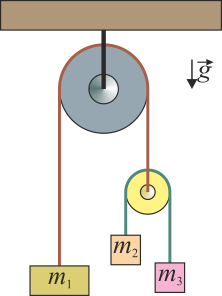
La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales (inextensibles y sin masa) y dos poleas también ideales (de masa despreciable y sin rozamiento).
- Escriba las ecuaciones de vínculo para las posiciones de las tres masas, medidas verticalmente hacia abajo desde la posición del centro de la polea grande. Escriba estos mismos vínculos en forma cinemática.
- Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.
7 Caja en pendiente
Una caja cúbica de gran masa desciende sin rozamiento por un plano inclinado un ángulo β. En el interior de la caja se encuentra un péndulo (de masa mucho menor que la de la caja) que cuelga de su techo.
- Si el péndulo no oscila, determine el ángulo θ que forma el péndulo con la vertical.
- Suponga ahora que entre la caja y el plano hay una fricción dinámica de coeficiente μ. Determine el ángulo de inclinación en ese caso.
- Para los dos casos anteriores, supóngase que el péndulo se separa ligeramente de su posición de equilibrio, ¿cuál será la frecuencia de las oscilaciones que experimenta?
8 Dos planos inclinados
Dos masas iguales de peso 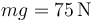 están situadas sobre dos planos inclinados contiguos fijos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.
Las masas están unidas por un resorte ideal de longitud natural nula y constante
están situadas sobre dos planos inclinados contiguos fijos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.
Las masas están unidas por un resorte ideal de longitud natural nula y constante 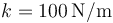 . No hay rozamiento con las superficies.
. No hay rozamiento con las superficies.
- Determine la posición de equilibrio de las dos masas, hallando los valores de x e y.
- Para esta posición de equilibrio, calcule las fuerzas de reacción ejercidas por los planos, así como la fuerza elástica que el resorte ejerce sobre cada masa.
- Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre las masas y las superficies en que se apoyan. En ese caso hay un rango de posiciones en las que puede producirse el equilibrio, ¿cuáles son los valores de (x,y) para los cuales puede haber equilibrio?
- Volviendo al caso sin rozamiento, determine las ecuaciones de movimiento para las dos masas.
Sugerencia: Empléense los ejes de la figura.
9 Anilla ensartada en dos varillas
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ésta de masa m,
- despreciando el peso,
- considerando el peso en la dirección de OY negativo.
Suponga que no hay rozamiento, por lo que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.

10 Partícula en un tubo
Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular ω constante alrededor del eje OZ
- Halle la ecuación diferencial que debe satisfacer la coordenada radial ρ sabiendo que el tubo no puede ejercer fuerza en la dirección longitudinal (no hay rozamiento).
- Calcule la solución de esta ecuación de movimiento si la partícula se encuentra inicialmente a una distancia A del eje de giro con velocidad radial nula.
- Halle la fuerza ejercida por el tubo para una posición y velocidades arbitrarias y para la solución anterior.
- Si se analiza este movimiento desde un sistema de referencia ligado al tubo ¿qué fuerzas actúan sobre la partícula? ¿Cuál de ellas acelera a la partícula? ¿Por qué aparece una fuerza del tubo sobre la partícula?
11 Masa que cuelga de dos hilos
Una masa de peso 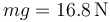 cuelga del techo suspendida de dos hilos de 65cm y 75cm de longitud, respectivamente, que están atados a dos puntos separados una distancia de 70cm.
cuelga del techo suspendida de dos hilos de 65cm y 75cm de longitud, respectivamente, que están atados a dos puntos separados una distancia de 70cm.
- Calcule la tensión de cada hilo en la posición de equilibrio.
- Suponga que se corta el hilo de 65cm, ¿cuál es la tensión del otro hilo justo tras el corte? ¿Cuál es la tensión de este hilo cuando la masa, en su movimiento pendular, pasa por la vertical?
- Suponga ahora que en lugar de ese hilo se corta el de 75cm, ¿cuál es la tensión del hilo restante justo tras el corte y cuando pasa por la vertical?
12 Varilla apoyada en una esquina
Dos masas iguales m están unidas por una varilla rígida ideal de longitud b. La varilla está apoyada en el suelo y en una pared vertical, formando la varilla un ángulo θ con la vertical. Todo el sistema está contenido en el plano vertical OXY
- Suponga que el sistema está en equilibrio. Calcule el mínimo valor que debe tener el coeficiente de rozamiento μ entre la varilla y el suelo para que esto ocurra. Para esta situación, ¿cuánto valen las reacciones normales del suelo y la pared, la fuerza de rozamiento y la tensión de la varilla?
- Suponga que no existe rozamiento y que la varilla va cayendo apoyada en el suelo y la pared. Para el momento en que la varilla forma un ángulo θ con la vertical y este ángulo varía con una velocidad
 , ¿cuánto valen las reacciones y la tensión?
, ¿cuánto valen las reacciones y la tensión?
- Determine la ecuación de movimiento para la varilla.
- Si inicialmente la varilla se encuentra en reposo en posición vertical y a partir de ahí comienza a deslizar, ¿para qué ángulo se separa de la pared?
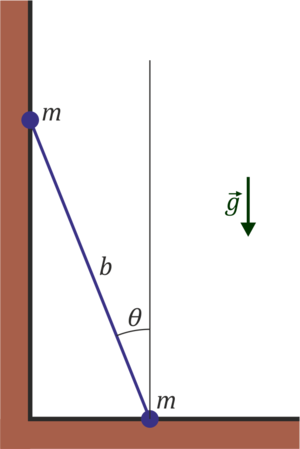
13 Varilla en cuchilla
Dos masas iguales m están unidas por una varilla rígida ideal de longitud b. La varilla reposa sobre un plano horizontal. una de masas (la “2”) puede deslizar sin rozamiento sobre el plano, pero la “1” está montada sobre una cuchilla que la obliga a desplazarse solo en la dirección paralela a la propia varilla
- ¿Qué vínculos ligan las posiciones y velocidades de las partículas? ¿De qué tipo es cada uno?
- ¿Hacia dónde van dirigidas las fuerzas de reacción vincular?
- Escriba el sistema de ecuaciones de movimiento y de vínculos para este sistema empleando como variables las coordenadas cartesianas de la masa 1 y el ángulo que la varilla forma con el eje OX.
- ¿Pueden reducirse las ecuaciones a un sistema de ecuaciones de primer orden en el que no aparezcan funciones trigonométricas?
14 Péndulo deslizante
Dos masas de valor m1 y m2 se encuentran unidas por una varilla rígida de longitud b y masa despreciable. m_1 puede deslizarse sin rozamiento sobre una superficie horizontal, mientras que m2 cuelga de la varilla pudiendo oscilar y moverse en el plano OXZ. Todo el sistema está sometido a la acción del peso.
- Empleando los procedimientos de la dinámica vectorial (es decir, considerando todas las fuerzas que actúan sobre cada masa), determine las ecuaciones de movimiento para las dos masas, en función del ángulo con la vertical θ y de la posición x de la masa m1.
- Determine dos constantes de movimiento en este problema. ¿Qué representan físicamente?
- Suponga que estando el péndulo vertical se aguanta la masa superior y la inferior se separa de la vertical un pequeño ángulo θ0.
- ¿A qué se reducen las ecuaciones de movimiento en ese límite
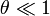 ?
?
- ¿Cuál es la frecuencia de oscilación? ¿A qué tiende en los casos
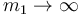 y
y 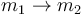 ?
?
- ¿A qué se reducen las ecuaciones de movimiento en ese límite
15 Varilla articulada
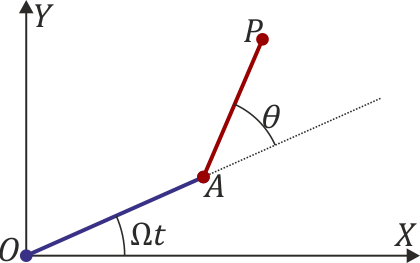
Se tiene un sistema horizontal en el que una partícula P, de masa m, se encuentra unida a una varilla de longitud 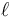 cuyo otro extremo, A, se halla articulado a una segunda varilla, de longitud b, cuyo segundo extremo, O, está fijo. La varilla OA gira en torno a O con velocidad angular constante Ω, mientras que la varilla AP puede girar libremente en torno a A. Sea θ el ángulo que AP forma con la prolongación de OA.
cuyo otro extremo, A, se halla articulado a una segunda varilla, de longitud b, cuyo segundo extremo, O, está fijo. La varilla OA gira en torno a O con velocidad angular constante Ω, mientras que la varilla AP puede girar libremente en torno a A. Sea θ el ángulo que AP forma con la prolongación de OA.
- ¿Qué vínculo hay entre las coordenadas cartesianas de P? Escríbalo en forma geométrica, cinemática y pfaffiana.
- Obtenga la ecuación de movimiento para el ángulo θ.
- ¿Qué puntos de equilibrio hay para el ángulo θ? ¿Son estables o inestables?





