Entrar Página Discusión Historial Go to the site toolbox

Partícula en alambre parabólico

De Laplace

Contenido

1 Enunciado

Una pequeña anilla de masa m está ensartada en un alambre de forma parabólica, situado en un plano vertical. Esta parábola tiene su vértice en O(0,0,0) y cuando la partícula se halla a una distancia b del eje, su altura es (b / 2), con b fijado. Este alambre parabólico se hace girar alrededor del eje con velocidad angular constante Ω. No hay rozamiento entre la anilla y el alambre

  1. Escriba las ecuaciones de vínculo para la posición de la anilla, en coordenadas cartesianas y en coordenadas cilíndricas. ¿De qué clase de vínculos se trata?
  2. Escriba las ecuaciones de vínculo en forma cinemática y en forma pfaffiana.
  3. Escriba las ecuaciones de movimiento para esta partícula, en cartesianas y en polares, incluyendo las fuerzas de reacción vincular necesarias.

2 Ecuaciones de vínculo

2.1 Forma parabólica

La parábola es de la forma, en cilíndricas

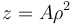
z= A \rho^2\,

Si imponemos que pase por el punto (b,b / 2) queda la ecuación

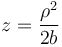
z=\frac{\rho^2}{2b}

Pasando a cartesianas

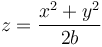
z=\frac{x^2+y^2}{2b}

o, equivalentemente

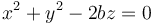
x^2+y^2-2bz=0\,

Este es un vínculo geométrico, bilateral, esclerónomo, liso y holónomo.

2.2 Rotación

Al estar en rotación, se cumple, en cilíndricas,

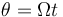
\theta=\Omega t\,

lo que nos da las coordenadas cartesianas

x=\rho\cos(\Omega t)\qquad\qquad y=\rho\,\mathrm{sen}(\Omega t)

Eliminamos ρ de estas ecuaciones y queda

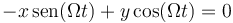
-x\,\mathrm{sen}(\Omega t)+y\cos(\Omega t)=0\,

Este es un vínuclo geométrico, bilateral, reónomo, liso y holónomo.

3 Vínculos en forma cinemática

3.1 Forma parabólica

Derivando respecto al tiempo y dividiendo por 2 obtenemos la forma cinemática

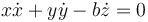
x\dot{x}+y\dot{y}-b\dot{z}=0

y, multiplicando por dt su forma pfaffiana

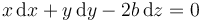
x\,\mathrm{d}x+y\,\mathrm{d}y-2b\,\mathrm{d}z=0

En cilíndricas partimos de

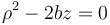
\rho^2-2bz=0\,

que da

\rho\dot{\rho}-b\dot{z}=0\qquad\Rightarrow\qquad \rho\,\mathrm{d}\rho-b\,\mathrm{d}z=0

3.2 Rotación

Derivando en la ecuación de vínculo

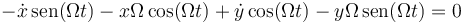
-\dot{x}\,\mathrm{sen}(\Omega t)-x\Omega\cos(\Omega t)+\dot{y}\cos(\Omega t)-y\Omega\,\mathrm{sen}(\Omega t)=0

Multiplicamos por dt

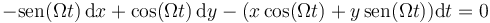
-\mathrm{sen}(\Omega t)\,\mathrm{d}x+\cos(\Omega t)\,\mathrm{d}y-(x\cos(\Omega t)+y\,\mathrm{sen}(\Omega t))\mathrm{d}t=0

En este caso, en cilíndricas queda claramente más simple

\dot{\theta}-\Omega = 0 \qquad\Rightarrow\qquad \mathrm{d}\theta-\Omega\,\mathrm{d}t=0
Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_en_alambre_parab%C3%B3lico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 00:56, 12 dic 2019. - Esta página ha sido visitada 727 veces. - Aviso legal - Acerca de Laplace