Cinemática del movimiento relativo (CMR)

De Laplace

Contenido

1 Introducción
2 Notación y definiciones
3 Sólidos vinculados. Pares cinemáticos
4 Derivación en ejes móviles. Fórmulas de Poisson
5 Composición de dos movimientos
6 Composición general de movimientos. Composiciones equivalentes
7 Composición de movimientos planos

1 Introducción

Cuando se estudia el movimiento de un único sólido rígido, se tiene la expresión general para el campo de velocidades

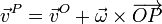
$\vec{v}^P = \vec{v}^O + \vec{\omega}\times\overrightarrow{OP}$

que nos dice que podemos conocer la velocidad de cada punto conocidos 6 datos: las 3 componentes del vector velocidad angular $\vec{\omega}$ y las 3 componentes de la velocidad de un punto arbitrario que tomamos como origen de coordenadas.

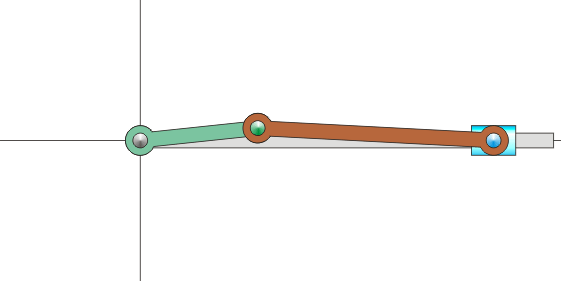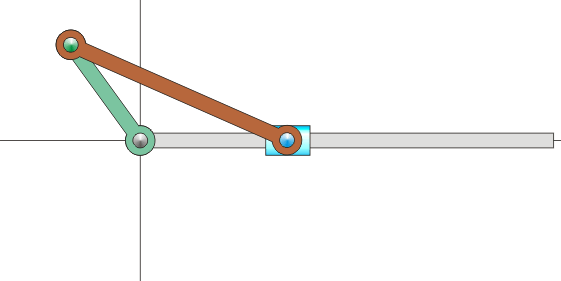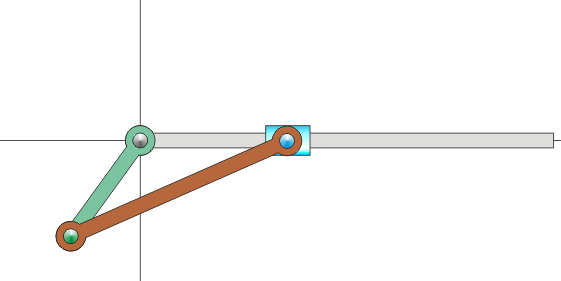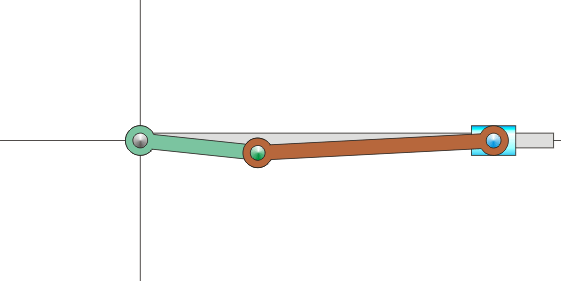
Sin embargo, en muchas situaciones, ni la velocidad angular ni la velocidad de O son datos inmediatos. Por ejemplo, consideremos el mecanismo sencillo de una biela y una manivela, como los que se encuentran dentro de un motor de explosión. Está formado por dos barras. Una, la manivela, gira en torno a uno de sus extremos, unido a un punto fijo. La segunda, la biela, tiene uno de sus extremos articulado al extremo móvil de la manivela, mientras que el otro está obligado a moverse en línea recta.

Es claro que, respecto a un sistema fijo, la manivela efectúa un movimiento de rotación, pero ¿qué movimiento realiza la biela en este mismo sistema? No es evidente de entrada, pues se desplaza a la vez que gira. Lo que sí sabemos es que, vista desde la manivela, la biela está girando respecto a su extremo.

Se trata entonces de hacer una composición de movimientos. El movimiento de la biela lo podemos describir como una rotación en torno a un extremo de la manivela, que a la vez gira en torno a su otro extremo respecto al sistema fijo.

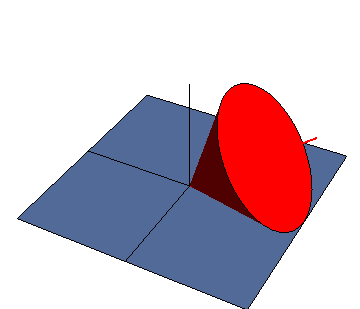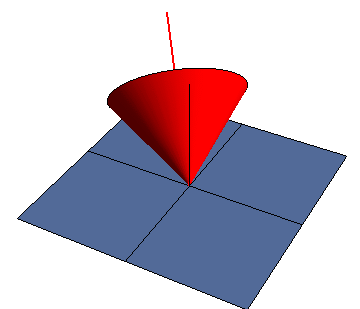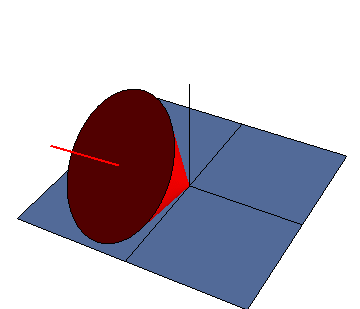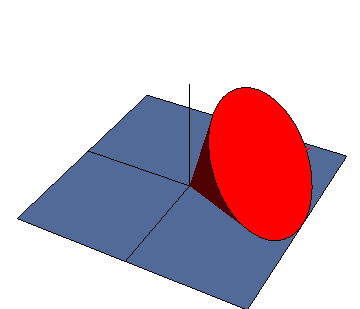
Un ejemplo tridimensional lo representa un cono que rueda sobre un plano. Podemos ver este movimiento como una rotación instantánea en torno a la recta de contacto entre el cono y el plano (pues los puntos de contacto tienen velocidad nula y forman el EIR) pero también puede verse como una composición de dos rotaciones, una en torno a un eje vertical y otra en torno al eje del cono.

En este tema veremos el tratamiento matemático de la descripción de movimientos de sólidos en varios sistemas de referencia simultáneos (movimientos relativos), así como la composición de dos o más movimientos rígidos para dar lugar a un movimiento neto.

2 Notación y definiciones

2.1 Sólidos y sistemas de referencia

El primer paso para estudiar el movimiento relativo consiste en generalizar el concepto de sólido rígido.

Normalmente, cuando uno piensa en un sólido rígido imagina un objeto amorfo, como una piedra, o moldeado, como una pieza de un mecanismo, pero en cualquier caso de tamaño finito. Cuando se habla de los puntos del sólido se piensa en los átomos que lo componen. No tendría sentido considerar punto del sólido a un lugar del espacio en el que no se encuentra el sólido en cuestión.

No obstante, tenemos una fórmula general para las velocidades del punto del sólido, que depende sólo de la posición del punto respecto a un cierto sistema de referencia, no de si en ese punto se encuentra una partícula material o no. Igualmente, la fórmula no requiere que se trate de un verdadero sólido rígido. Un sólido deformable, un líquido o un gas cuyos puntos se muevan según la fórmula anterior describe un movimiento rígido, aunque el medio material no sea indeformable.

Podemos extender entonces el concepto de sólido rígido, abstrayendo de su naturaleza material o finita, a un conjunto de puntos (que abarca todo el espacio) descrito por un cierto sistema de referencia, y tal que el campo de velocidades (y aceleraciones) es el correspondiente a un movimiento rígido

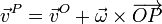
$\vec{v}^P = \vec{v}^O + \vec{\omega}\times\overrightarrow{OP}$

Si tenemos varios sólidos, a cada uno de ellos irá asociado un sistema de referencia y una distribución de velocidades para todos los puntos del espacio, independientemente de si forman parte del medio material o no. Es más, en la descripción de un problema aparecen usualmente sólidos intermedios que no poseen existencia material alguna. Usaremos las expresiones "sólido" y "sistema de referencia" de manera sinónima.

Un punto P del espacio no pertenecerá entonces a un sólido en concreto, sino a todos ellos simultáneamente.

Para poder visualizar este concepto podemos volver al ejemplo del mecanismo biela-manivela. El movimiento de este sistema transcurre en un plano, por lo que podemos prescindir de la tercera coordenada. El sistema se compone de tres sólidos: la barra fija (sólido 1), la manivela (sólido 0) y la biela (sólido 2). A cada uno de ellos podemos asociar un sistema de referencia en un plano. Podemos imaginar estos sistemas de referencia como hojas de papel superpuestas. Habrá una hoja de papel pegada a la barra. Sobre ella una hoja de papel unida a la manivela y sobre ésta una tercera hoja unida a la biela. Cada hoja se extiende a todo el plano. En cada instante, cada hoja se mueve respecto a las otras dos, aunque sigan superpuestas.

Un punto P del plano lo podemos imaginar como un alfiler que, en un instante dado, atraviesa simultáneamente las tres hojas de papel, de forma que tenemos un agujero en cada uno de las hojas, por ello decimos que el punto P está en los tres sólidos, aunque tenga vectores de posición diferentes en cada uno.

Cuando los sólidos se mueven unos respecto a los otros, la posición del punto P puede permanecer fija en alguno de los sólidos, pero cambiar en los otros. El punto P tendrá velocidad nula en uno de los sistemas de referencia y distinta de cero en los otros dos. Habrá situaciones, como el punto de articulación de la biela y la manivela, que tendrá velocidad nula en los sólidos 0 y 2, pero que estará en movimiento respecto al sólido 1.

Observemos que podemos hallar el estado de movimiento de, por ejemplo, la articulación de la biela con la barra, considerando esta articulación como parte del sólido 0 (la manivela) pese a que físicamente este punto no forme parte de la manivela. Debemos imaginarnos unos ejes solidarios con la manivela que llegan hasta este punto y determinar cómo se mueve un punto fijo en este sistema de referencia cuando la manivela efectúa sus movimiento de rotación respecto a la barra (o respecto a la biela).

En un sistema tridimensional la idea es exactamente la misma, aunque en lugar de hojas de papel superpuestas deberíamos imaginar volúmenes coincidentes que se mueven de distinta manera. Dado que esta idea es difícil de concebir, nos conformaremos con dibujar sistemas de ejes en movimiento relativo, pero manteniendo siempre en mente que los sólidos no son solo los ejes, sino todo el espacio.

Según esto, la pregunta ¿cuál es la velocidad del punto P? no tiene sentido. La pregunta siempre debe ser ¿cuál es la velocidad del punto P, considerado como parte del sólido i, respecto al sólido k?

2.2 Notación

Emplearemos la siguiente notación:

{ik}: movimiento del sólido i respecto al sólido k
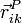
$\vec{r}^P_{ik}$: Posición de un punto P, considerado como parte del sólido i, respecto a un sistema de referencia ligado al sólido k. Nótese que en principio el primer subíndice parecería supérfluo, pues hemos dicho que un punto pertenece a todos los sólidos simultáneamente. Pero, cuando seguimos la evolución temporal de un punto material en concreto sí se hace importante saber a qué sólido pertenece, pues la trayectoria dependerá del sólido del que forme parte.
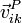
$\vec{v}^P_{ik}$: Velocidad de un punto P del sólido i respecto a un sistema ligado al sólido k.
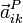
$\vec{a}^P_{ik}$: Aceleración de un punto P del sólido i respecto a un sistema ligado al sólido k.
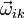
$\vec{\omega}_{ik}$: Velocidad angular del sólido i respecto al sólido k. Esta velocidad angular no lleva superíndice pues no está asociada a ningún punto en concreto, sino que es un vector libre, válido para todo el sólido.
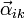
$\vec{\alpha}_{ik}$: Aceleración angular del sólido i respecto al sólido k.

El subíndice en las derivadas quiere decir que se deriva considerando que los ejes del sistema k permanecen fijos.

En el caso en que hay solo tres sólidos, son típicas los siguientes términos

Sólido de referencia o fijo: El etiquetado como 1. Nótese que esto no implica que este sólido se encuentre en un estado de reposo absoluto, inexistente, o siquiera que sea un sistema de referencia inercial.
Sólido problema: El etiquetado como 2.
Sólido intermedio: El etiquetado como 0.
Movimiento absoluto: El del sólido problema respecto al de referencia o fijo: {21}
Movimiento relativo: El del sólido problema respecto al sólido intermedio: {20}
Movimiento de arrastre: El del sólido intermedio respecto al de referencia: {01}

2.3 Sistemas de ejes

Cada sólido de un sistema lleva asociado un sistema de ejes coordenados. El sistema ligado al sólido $n$ se identificará por la presencia de un origen de coordenadas $O n$ y un conjunto de ejes ortogonales $O n X n$ , $O n Y n$ y $O n Z n$ .

Dados los tres ejes, existirá una base ortonormal ligada al sólido $n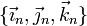$ , $\{\vec{\imath}_n,\vec{\jmath}_n,\vec{k}_n\}$ , formada por los vectores unitarios en la dirección de los ejes.

Esto quiere decir que un determinado vector (por ejemplo, la velocidad de un punto en concreto), podrá tener diferentes componentes, en el mismo instante, según el sólido al que lo estemos refiriendo, ya que la base vectorial será diferente de un sólido a otro.

Dado que la elección de ejes es arbitraria, cuando se estudia el estado de movimiento instantáneo de un sólido, a menudo podrán elegirse sistemas de ejes coincidentes instantáneamente, de manera que en ese momento las bases vectoriales son idénticas y las componentes de un vector son las mismas para todos los sólidos. Esta igualdad, no obstante, será solo momentánea, ya que debido al movimiento relativo, ejes y bases se habrán separado al instante siguiente. Esto es especialmente relevante a la hora de calcular derivadas respecto al tiempo.