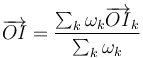Composición de movimientos planos (CMR)
De Laplace
1 Composiciones de velocidades y aceleraciones
Supongamos que tenemos tres sólidos “1”, “2” y “0” tales que los movimientos {20} y {01} son movimientos planos sobre el mismo plano director (o planos paralelos). En ese caso: La composición de dos movimientos planos paralelos entre sí es otro movimiento plano. Para todo punto P se verifica
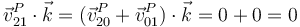
En este caso, la fórmula de composición de velocidades angulares se reduce a una suma de cantidades escalares
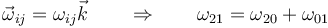
y lo mismo ocurre para la composición de aceleraciones angulares
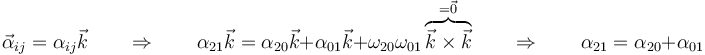
Por su parte, la composición de velocidades y aceleraciones se convierte en suma de vectores en el plano, que en muchas ocasiones puede realizarse gráficamente. Así, para la composición de aceleraciones tenemos
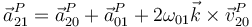
Gráficamente, el resultado del último producto corresponde a girar el vector 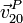 un ángulo de π\/2 en sentido antihorario.
un ángulo de π\/2 en sentido antihorario.
2 Teorema de los tres centros
En un movimiento plano de tres sólidos en el que los tres movimientos relativos son rotaciones existen tres centros instantáneos de rotación, Iij. En general se verifica el
- Teorema de los tres centros o de Aronhold-Kennedy
- Los tres centros instantáneos de rotación I21, I01 e I20 están alineados.
Para demostrar el teorema aplicamos la fórmula de composición de velocidades al CIR I21. Tenemos que
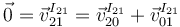
Las velocidades relativa y de arrastre de este punto valen

Sustituyendo en la velocidad absoluta queda
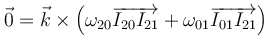
Dado que los dos vectores que se multiplican no pueden ser paralelos esto implica que
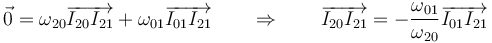
Por tanto, puesto que el vector que une I21 con I20 es proporcional al que lo une con I01, los tres puntos están alineados.
Podemos dar una relación entre las posiciones respecto a un punto de referencia. Si sustituimos en la relación anterior
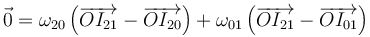
queda
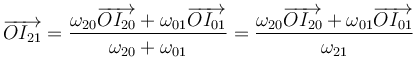
Vemos entonces que la posición del tercer centro es una media ponderada de las de los otros dos, siendo el peso de cada una la velocidad angular.
Si las dos velocidades van en el mismo sentido, el tercer centro estará en un punto intermedio del segmento. Si van en sentidos opuestos estará en la misma línea pero fuera del segmento.
Esta ley puede escribirse en la forma simétrica
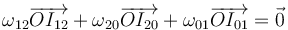
Así, por ejemplo, en el sistema biela-manivela,
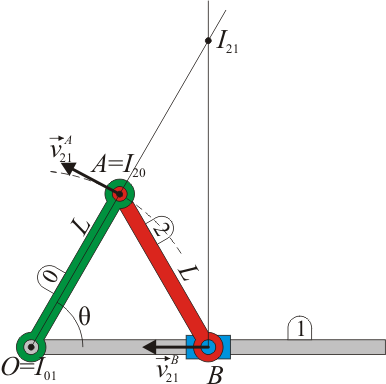
 se encuentra en la intersección de la recta que pasa por B y es perpendicular a
se encuentra en la intersección de la recta que pasa por B y es perpendicular a 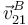 , con la recta que pasa por A y es perpendicular a
, con la recta que pasa por A y es perpendicular a 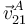 , pero esta última recta perpendicular es justamente la que pasa por O y A, que son los otros dos centros de rotación, por lo que los tres están alineados.
, pero esta última recta perpendicular es justamente la que pasa por O y A, que son los otros dos centros de rotación, por lo que los tres están alineados.Este resultado es generalizable al caso de que alguno de los movimientos sea una traslación. Supongamos que el movimiento de arrastre {01} es una traslación con velocidad de traslación 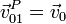 . En ese caso tenemos
. En ese caso tenemos
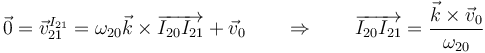
Por tanto, la línea que une los centros I20 e I21 es perpendicular a la velocidad de traslación  , en cuyo “extremo” se encuentra el CIR I01 (que, por ser una traslación, es un punto del infinito).
, en cuyo “extremo” se encuentra el CIR I01 (que, por ser una traslación, es un punto del infinito).
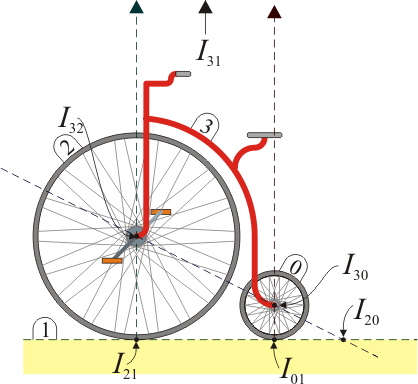
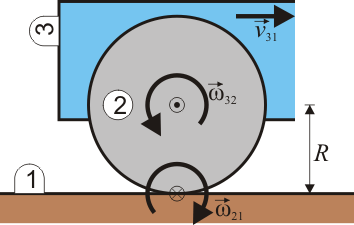
Como ilustración consideremos el caso de un carro “3” cuya rueda “2” se encuentra rodando sobre el suelo horizontal “1”.
El teorema de los tres centros permite determinar gráficamente la posición de los centros instantáneos de rotación de sistemas de más de tres sólidos, a partir del conocimiento de algunos de ellos.
- Sólido 0
- La rueda trasera
- Sólido 1
- El suelo
- Sólido 2
- La rueda delantera
- Sólido 3
- El cuadro del velocípedo
Las dos ruedas realizan, respecto del cuadro “3”, movimientos de rotación alrededor de sus respectivos ejes. Por ello, el CIR I32 es el centro de la rueda delantera “2” y el CIR I30 el de la trasera “0”.
Respecto del suelo “1” cada rueda efectúa una rotación instantánea alrededor del punto de contacto. Por ello, el punto de apoyo de la rueda delantera es el CIR I21 y el de la trasera es el I01.
Nos preguntamos entonces por la posición del CIR I20, esto es, desde un sistema solidario con la rueda trasera, ¿alrededor de que punto gira la delantera? Por el teorema de los tres centros, I20 se encuentra alineado con I21 y con I01. Por tanto, debe encontrarse sobre la línea horizontal del suelo. Por el mismo teorema, I20 debe estar alineado con I32 y con I30, lo que supone que debe hallarse en la recta que une los centros de las dos ruedas. Por ello, debe encontrarse en la intersección de esta recta con la horizontal del suelo. El resultado es un punto que no pertenece al sólido real “0” ni al “2”, sino que se encuentra a una cierta distancia por detrás del vehículo.
Podemos preguntarnos también por la ubicación del CIR I31, correspondiente al movimiento del cuadro respecto al suelo. Este CIR se encuentra alineado, por un lado con los centros I30 e I01, y por otro con los centros I32 e I21. Estas dos rectas, sin embargo, son paralelas, ya que ambos pares de puntos se encuentran sobre sendas verticales. El CIR I31 se encuentra por tanto en el infinito, sobre una dirección perpendicular a la horizontal. Esto corresponde a que el cuadro realiza un movimiento de traslación cuya velocidad es horizontal, indicando el avance del velocípedo.2.1 Cálculo analítico del CIR de una composición
Supongamos que tenemos una composición de movimientos {21}={20}+{01} y conocemos los centros instantáneos de rotación y las velocidades angulares, supuestas no nulas, de los movimientos relativos y de arrastre. Si deseamos hallar la posición del CIR del movimiento absoluto, I21, respecto a un cierto punto O, la fórmula analítica general nos da
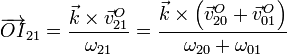
Las velocidades relativa y de arrastre corresponden a sendas rotaciones
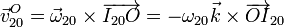
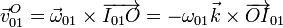
Llevando esto a la expresión analítica anterior y empleando las propiedades del doble producto vectorial queda
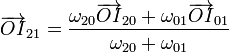
Se trata entonces de una media ponderada de los dos vectores de posición relativos de cada uno de los CCIIR individuales.
- Si las dos rotaciones son en el mismo sentido, el CIR I21 se encuentra en el segmento con extremos los otros dos CCIIR, estando más cerca del correspondiente a una mayor velocidad angular. Si las dos son iguales se encuentra en el punto medio del segmento.
- Si las dos rotaciones son en sentido opuesto, se encuentra en la recta que pasa por I20 e I01, pero en la parte exterior al segmento que une a estos dos puntos. De nuevo se encuentra más cerca del correspondiente a la velocidad angular de mayor magnitud. Si las dos rotaciones son iguales y opuestas la composición se reduce a una traslación y el CIR I21 se va al infinito.
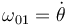
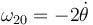

por lo que la posición del CIR I21 viene dada por
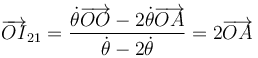
Esta fórmula es fácilmente generalizable a la composición de N rotaciones. Basta hallar la media ponderada de los centros de los diferentes movimientos relativos