Fórmulas de Poisson (CMR)
De Laplace
El que la velocidad de un punto pueda ser cero en un sistema de referencia y no nula en otro muestra que la derivada respecto al tiempo depende del sistema de referencia, que debe ser indicado explícitamente.
Este problema no aparece con las derivadas de las cantidades escalares, cuyo valor es el mismo para todos los sistemas de referencia. La cuestión surge con las magnitudes vectoriales (y tensoriales, que no consideraremos) debido a que los propios vectores de la base son funciones del tiempo, al moverse un sistema de referencia respecto a otro.
1 Derivada temporal en una base
Definimos la derivada temporal de una magnitud vectorial 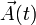 en un
sistema 1, como la que se obtiene, aplicando las reglas habituales de derivación,
admitiendo que los vectores de la base asociada a dicho sistema permanecen constantes, esto es, si
en un
sistema 1, como la que se obtiene, aplicando las reglas habituales de derivación,
admitiendo que los vectores de la base asociada a dicho sistema permanecen constantes, esto es, si
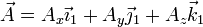
su derivada temporal en el sistema 1 es
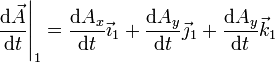
Nótese que las derivadas de las componentes, que son cantidades escalares, no precisan subíndice.
La posición y las velocidades y aceleraciones definidas en la sección anterior son, en principio, magnitudes instantáneas, esto es, nos informan de la posición, velocidad y aceleración de un punto en concreto, o de todos los puntos de un sólido en un instante dado. Como tales no son, en principio, derivables respecto al tiempo (ya que una derivada implica una diferencia entre los valores en dos instantes diferentes).
No obstante lo anterior, cuando se estudia un movimiento relativo de un sólido respecto a otro a lo largo del tiempo, en ocasiones es posible determinar la posición de un punto material concreto como función del tiempo, 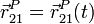 . En ese caso sí podemos calcular sus derivadas. Definimos la velocidad y la aceleración de un punto P (que tomamos como perteneciente al sólido 2, aunque puede tratarse de una simple partícula material), tal como se miden en el sistema 1 como
. En ese caso sí podemos calcular sus derivadas. Definimos la velocidad y la aceleración de un punto P (que tomamos como perteneciente al sólido 2, aunque puede tratarse de una simple partícula material), tal como se miden en el sistema 1 como
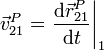
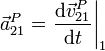
Asimismo, el movimiento relativo de un sólido respecto a otro viene caracterizado además de por la velocidad y aceleración de un punto material concreto, por la velocidad y aceleración angulares, cumpliéndose
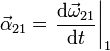
2 Relación entre derivadas temporales
Supongamos que tenemos una cierta cantidad vectorial 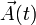 de la que
hemos calculado, en un instante t0, su derivada temporal en dos sistemas de referencia 0 y 1, y queremos relacionar estas dos cantidades. Cualquier vector tendrá una cierta expresión en cada una de las bases vectoriales correspondientes a los diferentes sólidos.
de la que
hemos calculado, en un instante t0, su derivada temporal en dos sistemas de referencia 0 y 1, y queremos relacionar estas dos cantidades. Cualquier vector tendrá una cierta expresión en cada una de las bases vectoriales correspondientes a los diferentes sólidos.
Partimos de la expresión en la base ligada al sólido “0”
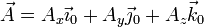
Si derivamos  respecto al tiempo en el sistema 1
respecto al tiempo en el sistema 1
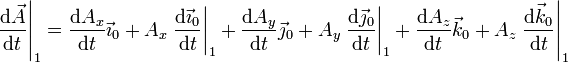
Necesitamos entonces conocer la derivada temporal de los vectores de la base. El vector
unitario 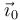 es el que une al origen de coordenadas, O, con un punto A,
situado a una distancia unidad a lo largo del eje X0. Su derivada es
es el que une al origen de coordenadas, O, con un punto A,
situado a una distancia unidad a lo largo del eje X0. Su derivada es
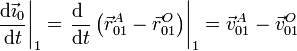
Aplicando la expresión del campo de velocidades de un sólido
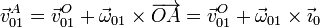
llegamos a
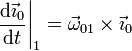
A este mismo resultado se llega directamente empleando la equiproyectividad del campo de velocidades y es justamente la propiedad que permite definir la velocidad angular del sólido, de acuerdo con la demostración del Teorema de Chasles.
Análogamente tenemos, para los otros dos vectores
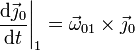
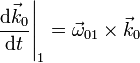
Estas tres igualdades se conocen como fórmulas de Poisson.
Sustituyendo y reordenando términos nos queda
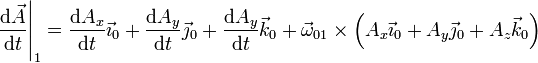
que equivale a
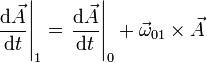
Esta igualdad también se conoce como fórmula de Poisson y contiene como casos particulares a las expresiones correspondientes a los vectores de la base.
Esta identidad es aplicable a cualquier magnitud vectorial, lo que incluye a las posiciones, velocidades y las propias velocidades angulares.





