El vector de posición y otros ejemplos
De Laplace
1 Vector de posición
Como primer ejemplo de vector expresado en los tres sistemas veremos el propio vector de posición, que une el origen de coordenadas con el punto  . Lo hemos expresado en cartesianas. Lo escribimos de nuevo empleando la notación
. Lo hemos expresado en cartesianas. Lo escribimos de nuevo empleando la notación 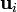
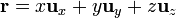
Para escribirlo en cilíndricas, puede existir la tentación de ponerlo como 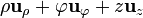 pero estaría mal, rotundamente mal. Para empezar porque este vector ni siquiera es dimensionalmente correcto, ya que suma una distancia (medida en metros) con un ángulo (medido en radianes). La forma correcta es
pero estaría mal, rotundamente mal. Para empezar porque este vector ni siquiera es dimensionalmente correcto, ya que suma una distancia (medida en metros) con un ángulo (medido en radianes). La forma correcta es
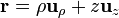
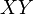 , que va desde el origen hasta la proyección de
, que va desde el origen hasta la proyección de 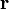 sobre dicho plano,
sobre dicho plano, 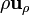 y otro que une este punto con el final,
y otro que une este punto con el final, 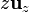 . Comparando estos dos resultados tenemos la relación adicional
. Comparando estos dos resultados tenemos la relación adicional
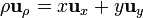
En esféricas, la expresión es aún más sencilla. Puesto que 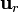 es el unitario en la dirección radial, el vector
es el unitario en la dirección radial, el vector 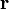 se obtiene simplemente multiplicando este unitario por el módulo de
se obtiene simplemente multiplicando este unitario por el módulo de 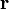
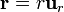
Antes dijimos que esta expresión es mucho más sencilla que empleando la base cartesianas, y es cierto, pero no hay que pensar que porque  y
y 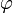 han desaparecido de la ecuación, este vector ya no depende de esas dos coordenadas. Sí, lo hace, sólo que la dependencia está escondida en
han desaparecido de la ecuación, este vector ya no depende de esas dos coordenadas. Sí, lo hace, sólo que la dependencia está escondida en 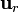 , ya que
, ya que
Reuniendo los tres resultados
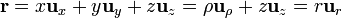
2 Otro cambio de base
Supongamos un vector sin interpretación geométrica, por ejemplo
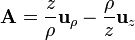
¿Cómo se escribe este vector en cartesianas? Primero cambiamos de base, aplicando las relaciones entre las bases
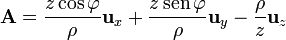
y a continuación sustituimos las coordenadas, empleando las relaciones correspondientes
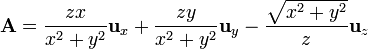
Si en lugar de a cartesianas queremos pasar a esféricas podemos cambiar primero las coordenadas
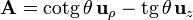
y, a continuación, cambiamos de base,

vemos que un vector que se expresa de forma sencilla en un sistema puede ser muy complejo en otro diferente. Normalmente aparecen raíces cuadradas de lo más molestas.
3 Enlaces
- Siguiente: Diferenciales
- Anterior: Tabla de factores de escala






