Campo magnético de un cable cilíndrico
De Laplace
Contenido |
1 Enunciado
Calcule el campo magnético producido en todo el espacio por un cable cilíndrico de radio a y longitud infinita, por el cual circula una densidad de corriente uniforme  en la dirección de su eje.
en la dirección de su eje.
2 Introducción
Para este sistema, las leyes de la magnetostática nos dicen
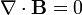

A la hora de hallar el campo, podemos emplear un razonamiento casi idéntico al que se usa en el caso de un hilo infinito. Al igual que en ese sistema puede demostrarse que
- Las componentes del campo magnético no dependen de la coordenada z (simetría traslacional).
- Las componentes del campo magnético no dependen de la coordenada
 (simetría acimutal).
(simetría acimutal).
- La componente Bz, por ser el campo magnético ortogonal a la corriente que lo crea.
- La componente Bρ es nula, como consecuencia de la ley de Gauss para el campo magnético.
Por todo ello  se reduce a
se reduce a

La diferencia aparece al aplicar la ley de Ampère. Si consideramos una circunferencia Γ de radio ρ centrada en el cable y la cantidad de corriente I que atraviesa una superficie apoyada en ella, tenemos dos casos:
3 Puntos exteriores al cable
Si ρ > a, la corriente I es la total del cable:
y de aquí

esto es, el campo que produce el cable en su exterior es igual que el produciría un hilo infinitamente delgado situado en el centro del cable.
4 Puntos interiores al cable
Si ρ < a, la corriente I(ρ) es solamente la abarcada por un círculo que tiene a Γ por borde
y de aquí

En el interior el campo crece linealmente con ρ, la distancia al eje. El campo máximo se alcanza justo en la superficie del hilo y vale μ0I / 2πa. Para  y
y 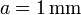 vale 0.2 mT
vale 0.2 mT







