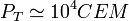Problemas del primer principio de la termodinámica
De Laplace
1 Trabajo en diferentes procesos
2 Calorímetro de flujo
3 Temperatura de una llama
4 Temperatura de un vaso metálico
5 Mezcla de agua y hielo
6 Mezcla de agua y vapor
7 Mezcla de agua y hielo con bloque metálico
8 Aleación de dos metales
9 Transformación de energía potencial gravitatoria en calor
Un bloque de hielo a 0oC se deja caer libremente desde una altura de 80 m. En el momento del choque, un 20% de la energía del bloque se transforma en calor absorbible por su masa. ¿Que parte del hielo se funde a causa de esta absorción?
10 Conducción térmica en dos barras en contacto
Una barra de oro está en contacto térmico con otra de plata de la misma longitud y área. Uno de los extremos de esta barra compuesta se mantiene a una temperatura de 80oC, mientras que el extremo opuesto está a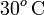 
. Cuando la transferencia de energía alcance un estado estacionario, ¿cuál será la temperatura en la unión?
Datos: conductividad térmica del oro: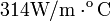 
;
conductividad térmica de la plata: 
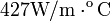
11 Crecimiento de una capa de hielo
Un estanque de agua a 0oC está cubierto por una capa de hielo de 4.00 cm de espesor. Si la temperatura del aire permanece constante a -10.0oC, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm?
12 Potencia radiada por el Sol
La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a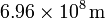 
.
Calcule la energía total radiada por el Sol cada segundo si la emisividad es e = 0.965. Calcule la potencia que llega a la superficie
de la Tierra, si el radio de esta es 
, y la distancia media Tierra-Sol es
.
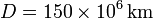Solución La potencia emitida por una superficie irradiante es
P = σAeT4
donde T es la temperatura absoluta,e es la emisividad de la superficie, A es el área de la superficie
emisora y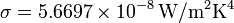 
es la constante de Stefan-Boltzmann.
En nuestro caso la superficie emisora es la del Sol. A partir de su radio podemos calcularla
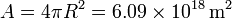
Con los dos datos del problema podemos calcular la potencia radiada por el Sol
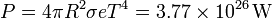
Para calcular la fracción de esta potencia recibida por la Tierra, consideramos la esfera con centro en el Sol y de radio la distancia media entre el Sol y la Tierra. La superficie de esta esfera es
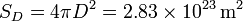
La potencia total emitida por el Sol se distribuye uniformemente sobre esta superficie. La fracción de esta potencia recibida por el Sol es igual a la fracción de la superficie que la Tierra ofrece al Sol respecto a SD. Esta fracción es
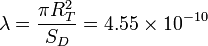
No aparece el factor 4 porque el Sol ve a la Tierra esencialmente como un disco plano de radio RT. Así, pues la potencia recibida por la superficie de la Tierra es
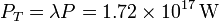
Podemos comparar esta potencia con el consumo energético medio mundial. En el año 2005 este consumo fue
.
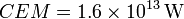Por tanto, la potencia que recibe la Tierra es
