Problemas de cinemática tridimensional de la partícula (GIOI)

De Laplace

1 Anilla ensartada en dos varillas

Una pequeña anilla P se encuentra ensartada en la intersección de dos barras giratorias. Los extremos fijos de las barras distan una cantidad 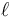y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:

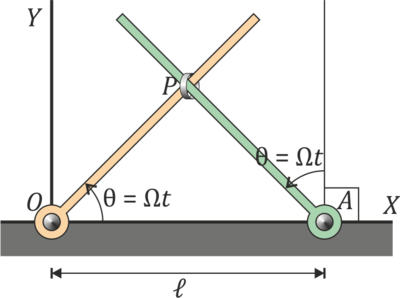
1. ¿Cuáles son las ecuaciones horarias de P?
2. ¿Qué clase de trayectoria describe?
3. ¿Qué tipo de movimiento realiza?

Solución

2 Movimiento en un tiro parabólico

Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

una posición inicial nula (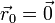) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v₀.

1. Determine el vector de posición, la velocidad y la aceleración en cada instante.
2. Halle el punto donde la partícula impacta con el suelo. ¿Cuál es el alcance máximo para una rapidez inicial dada?
3. Calcule la celeridad y el vector tangente en el instante inicial y en el instante en que se encuentra a mayor altura.
4. Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los dos instantes anteriores.
5. Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
6. Suponga que se quiere alcanzar un blanco situado a 60 m con un mortero que comunica una rapidez inicial de 25 m/s. ¿Con qué ángulo debe dispararse si en medio se encuentra un eucalipto de 15 m de altura? (supóngase )

Solución

3 Tiro parabólico sobre una pendiente

Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.

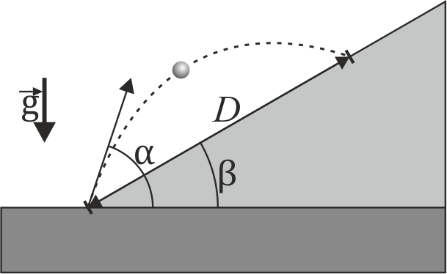
1. ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
2. Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
   1. La rapidez que tiene en el momento del impacto.
   2. La aceleración tangencial y normal (escalares) en el momento de impacto.

Tómese .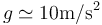

Solución

4 Estudio de un movimiento tridimensional

Una partícula se mueve según las ecuaciones horarias

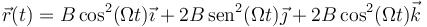
1. ¿Qué trayectoria sigue la partícula?
2. Determine la ley horaria s(t). Suponga que s(0) = 0.
3. ¿Qué tipo de movimiento describe la partícula?

Solución

5 Velocidad y aceleración en puntos terrestres

La Tierra la podemos modelar como una esfera de 6370 km de radio. Determine la rapidez y la aceleración normal (expresada en unidades de g) para un punto del ecuador terrestre debida al movimiento de rotación terrestre. ¿Cuánto valen la rapidez y aceleración normal en Sevilla (latitud 37°24′40″N)?

Solución

6 Velocidad y aceleración orbital de la Tierra

La órbita terrestre es aproximadamente circular con un radio 1UA = 149.60Gm. ¿Cuánto vale la rapidez y la aceleración normal de la Tierra en su movimiento orbital?

Solución

7 Movimiento circular en 3D

Una partícula se mueve según las ecuaciones horarias

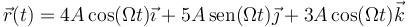
con A y Ω constantes.

1. ¿Qué trayectoria sigue la partícula?
2. ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
3. Justifique que este movimiento es circular y uniforme
4. Determine la posición del centro del movimiento circular
5. Calcule la velocidad angular de este movimiento circular

Solución