Problemas de cinemática del movimiento rectilíneo (GIOI)
De Laplace
Contenido |
1 Posición dependiente del tiempo
Una partícula se mueve de manera que su posición como función del tiempo está representada en la gráfica de la figura
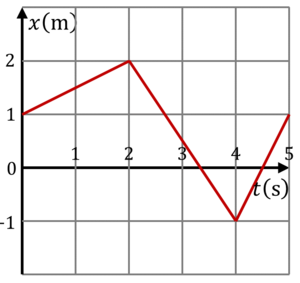
- ¿Cuánto vale su desplazamiento entre
y 
?
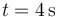- ¿Cuánto vale la distancia total recorrida en el mismo intervalo?
- ¿Cuánto vale el desplazamiento y la distancia total recorrida en el intervalo (0 s,5 s)?
- ¿Cuánto vale la velocidad media en los intervalos (0 s,5 s), (0 s,4 s) y (2 s,5 s)?
- ¿Cómo es la gráfica de la velocidad instantánea como función del tiempo?
2 Persecución policial
Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?
Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?
3 Análisis numérico de movimiento
La posición de una partícula en distintos instantes de tiempo es, aproximadamente
| t (s) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
|---|---|---|---|---|---|---|---|
| x (m) | −1.728 | −0.440 | 0.560 | 1.296 | 1.792 | 2.072 | 2.160 |
| t (s) | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 |
|---|---|---|---|---|---|---|---|
| x (m) | 2.080 | 1.856 | 1.512 | 1.072 | 0.560 | 0.000 | −0.584 |
| t (s) | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
|---|---|---|---|---|---|---|---|
| x (m) | −1.168 | −1.728 | −2.240 | −2.680 | −3.024 | −3.248 | −3.328 |
Para este movimiento, halle:
- El desplazamiento entre
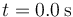y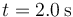 
, así como el valor aproximado de la distancia recorrida en dicho intervalo.
- La velocidad media y la rapidez media en el intervalo anterior.
- La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
- El valor aproximado de la velocidad en
.
- El valor aproximado de la aceleración en .
- Sabiendo que este movimiento sigue una ley de la forma
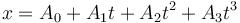
- Calcule
- Los valores de las constantes Ak.
- El valor exacto de la distancia recorrida y la rapidez media.
- El valor exacto de la velocidad y de la aceleración en .
4 Rapidez de impacto
Una partícula está sometida exclusivamente a la acción de la gravedad. Si se lanza con velocidad + v0 en dirección vertical hacia arriba desde un punto de altura h. ¿Cuál es su velocidad cuando llega al suelo? Si en vez de lanzarse hacia arriba se lanza hacia abajo, con velocidad − v0, ¿llegará con una rapidez mayor?
5 Calculo de magnitudes a partir de v(t)
Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI
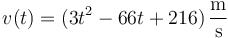
entre y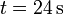 
. La posición inicial es 
. Halle:
- La posición de la partícula en cada instante del intervalo indicado.
- La velocidad media de la partícula en este intervalo.
- Los valores máximo y mínimo de x.
- La distancia recorrida en ese intervalo y la rapidez media.
- Los valores máximo y mínimo de la velocidad y la rapidez.
- La aceleración en todo instante.
6 Calculo gráfico de velocidad media
La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.
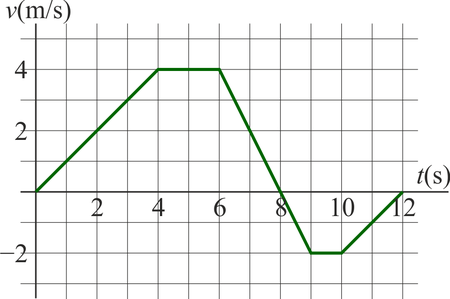
- ¿Cuánto vale aproximadamente la velocidad media entre y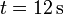
?
- ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?
- De los cuatro instantes siguientes, ¿en cual la aceleración tiene el mayor valor absoluto? (a) 0.0 s; (b) 5.0 s; (c) 8.0 s; (d) 9.5 s.
