Primera Prueba de Control 2018/19 (G.I.E.R.M.)

De Laplace

1 Partículas en colisión

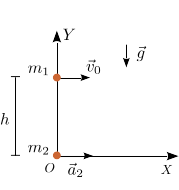
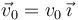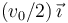Una partícula de masa m₁ se lanza desde una altura h con velocidad horizontal , con v₀ > 0. La partícula se mueve bajo la acción de la gravedad. Se desprecia el rozamiento del aire. Al mismo tiempo, otra partícula de masa m₂ parte desde el origen con velocidad inicial . Esta partícula se mueve sobre el eje OX con aceleración .

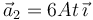1. Escribe el vector de posición de la partícula 1 en función del tiempo.
2. Escribe el vector de posición de la partícula 2 en función del tiempo
3. Suponiendo que 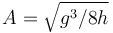, calcula el vector tangente de la trayectoria seguida por la partícula 1 en el instante de la colisión.

2 Dos masas con muelle y rozamiento

Las masas m₁ y m₂ se disponen como se indica en la figura. El contacto entre las masas es rugoso, con coeficiente de rozamiento estático μ. El contacto entre la masa m₂ y el suelo es liso. La masa m₁ está conectada a un muelle de constante elástica k y longitud natural nula. El muelle se mantiene siempre horizontal. La gravedad actúa como se indica en la figura. El movimiento se produce de tal manera que en todo instante 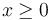.