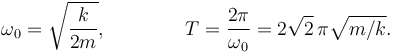De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

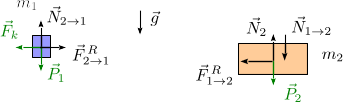
Las masas $m 1$ y $m 2$ se disponen como se indica en la figura. El contacto entre las masas es rugoso, con coeficiente de rozamiento estático $μ$ . El contacto entre la masa $m 2$ y el suelo es liso. La masa $m 1$ está conectada a un muelle de constante elástica $k$ y longitud natural nula. El muelle se mantiene siempre horizontal. La gravedad actúa como se indica en la figura. El movimiento se produce de tal manera que en todo instante 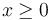$x\geq 0$ .

Dibuja los diagramas de cuerpo libre de cada masa en la situación de la figura. En este caso se conocen los sentidos de todas las fuerzas que actúan, por lo que hay que indicarlos correctamente en el diagrama.
Suponiendo que las masas se mueven como un bloque, encuentra las expresiones de todas las fuerzas que actúan en el sistema.
Supongamos que las dos masas son iguales, $m 1 = m 2 = m$ . ¿Que condición debe cumplir $x$ para que la masa $m 1$ no deslice respecto a $m 2$ ?
Supongamos que se cumple en todo instante la condición de la pregunta anterior y las masas se mueven siempre juntas. Manteniendo que $m 1 = m 2 = m$ , ¿cual es el período de las oscilaciones de las masas?

2 Solución

2.1 Fuerzas sobre las masas

La figura de la derecha muestra las fuerzas que actúan con su masa, con la dirección y sentido indicadas. Para la masa $m 1$ tenemos

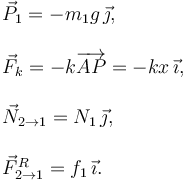
$\begin{array}{l} \vec{P}_1 = -m_1g\,\vec{\jmath}, \\ \\ \vec{F}_k = -k\overrightarrow{AP} = -kx\,\vec{\imath},\\ \\ \vec{N}_{2\to1} = N_1\,\vec{\jmath},\\ \\ \vec{F}_{2\to1}^R = f_1\,\vec{\imath}. \end{array}$

La fuerza de rozamiento apunta hacia la derecha pues, si no hubiera rozamiento entre las masas, el muelle tiraría de la masa 1 hacia la izquierda, pues su longitud natural es nula.

Para la masa $m 2$ tenemos

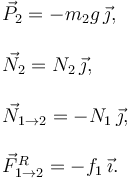
$\begin{array}{l} \vec{P}_2 = -m_2g\,\vec{\jmath}, \\ \\ \vec{N}_{2} = N_2\,\vec{\jmath},\\ \\ \vec{N}_{1\to2} = -N_1\,\vec{\jmath},\\ \\ \vec{F}_{1\to2}^R = -f_1\,\vec{\imath}. \end{array}$

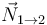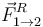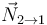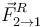Hemos usado que las fuerzas $\vec{N}_{1\to2}$ y $\vec{F}^R_{1\to2}$ son pares de acción-reacción de $\vec{N}_{2\to1}$ y $\vec{F}^R_{2\to1}$ , respectivamente.

Las masas están en movimiento, por lo que hemos de aplicar la Segunda Ley de Newton a cada una de las masas. Para $m 1$ tenemos

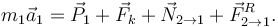
$m_1\vec{a}_1 = \vec{P}_1 + \vec{F}_k + \vec{N}_{2\to1} + \vec{F}_{2\to1}^R.$

De aquí obtenemos dos ecuaciones escalares

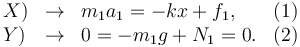
$\begin{array}{lclr} X) & \to & m_1a_1 = -kx + f_1, & (1)\\ Y) & \to & 0 = -m_1g + N_1 = 0. & (2) \end{array}$

Para la masa 2 tenemos

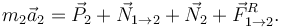
$m_2\vec{a}_2 = \vec{P}_2 + \vec{N}_{1\to2} + \vec{N}_2 + \vec{F}_{1\to2}^R.$

De aquí obtenemos otras dos ecuaciones escalares

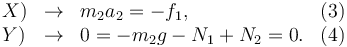
$\begin{array}{lclr} X) & \to & m_2a_2 = -f_1, & (3)\\ Y) & \to & 0 = -m_2g - N_1 + N_2 = 0. & (4) \end{array}$

De las ecuaciones (2) y (4) obtenemos

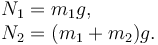
$\begin{array}{l} N_1 = m_1g, \\ N_2 = (m_1+m_2)g. \end{array}$

Si, como dice el enunciado las dos masas se mueven juntas, tenemos

$a 1 = a 2 = a .$

Sumando las ecuaciones (1) y (3) tenemos

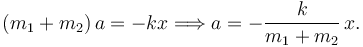
$(m_1 +m_2)\,a = -kx \Longrightarrow a = -\dfrac{k}{m_1+m_2}\,x.$

Ahora podemos despejar $f 1$ de la ecuación (3). Finalmente, las fuerzas vinculares que actúan en el sistema son

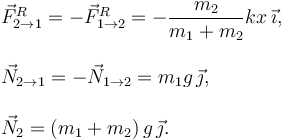
$\begin{array}{l} \vec{F}^R_{2\to1} = -\vec{F}^R_{1\to2} = -\dfrac{m_2}{m_1+m_2}kx\,\vec{\imath},\\ \\ \vec{N}_{2\to1} = -\vec{N}_{1\to2} = m_1g\,\vec{\jmath},\\ \\ \vec{N}_2 = (m_1+m_2)\,g\,\vec{\jmath}. \end{array}$

2.2 Condición de no deslizamiento

Para que la masa 2 no deslice sobre la 1 tiene que ocurrir que la fuerza de rozamiento entre las dos masas no supere el valor máximo que puede alcanzar. Si las dos masas son iguales $m 1 = m 2 = m$ tenemos

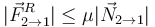
$|\vec{F}^R_{2\to1}| \leq \mu|\vec{N}_{2\to1}|$

Si las dos masas son iguales $m 1 = m 2 = m$ tenemos

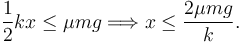
$\dfrac{1}{2}kx \leq \mu mg \Longrightarrow x\leq \dfrac{2\mu mg}{k}.$

2.3 Período de las oscilaciones

Cuando se cumplen las condiciones del apartado anterior la ecuación de la aceleración se escribe

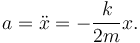
$a = \ddot{x} = -\dfrac{k}{2m}x.$

Esta es la ecuación de un oscilador armónico con frecuencia angular y período

$\omega_0 = \sqrt{\dfrac{k}{2m}}, \qquad\qquad T = \dfrac{2\pi}{\omega_0} = 2\sqrt{2}\,\pi\sqrt{m/k}.$

Dos masas con muelle y rozamiento, Noviembre 2018 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre las masas

2.2 Condición de no deslizamiento

2.3 Período de las oscilaciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES