De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

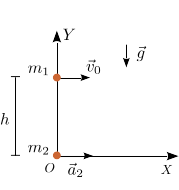
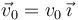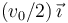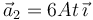Una partícula de masa $m 1$ se lanza desde una altura $h$ con velocidad horizontal $\vec{v}_0=v_0\,\vec{\imath}$ , con $v 0 > 0$ . La partícula se mueve bajo la acción de la gravedad. Se desprecia el rozamiento del aire. Al mismo tiempo, otra partícula de masa $m 2$ parte desde el origen con velocidad inicial $(v_0/2)\,\vec{\imath}$ . Esta partícula se mueve sobre el eje $O X$ con aceleración $\vec{a}_2 = 6At\,\vec{\imath}$ .

Escribe los vectores de posición de las dos partículas en función del tiempo.
¿Cuál debe ser el valor de $v 0$ para que las partículas colisionen en el eje $O X$ ?
Suponiendo que 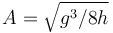$A=\sqrt{g^3/8h}$ , calcula el vector tangente de la trayectoria seguida por la partícula 1 en el instante de la colisión.

2 Solución

2.1 Movimientos de las partículas

La partícula realiza un movimiento parabólico. El movimiento es uniforme sobre el eje $O X$ y uniformemente acelerado sobre el eje $O Y$ . El movimiento sobre el eje $O X$ es

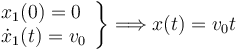
$\left. \begin{array}{l} x_1(0) = 0\\ \dot{x}_1(t) = v_0 \end{array} \right\} \Longrightarrow x(t) = v_0t$

El movimiento sobre el eje $O Y$ es

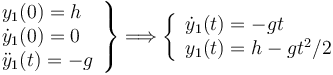
$\left. \begin{array}{l} y_1(0) = h\\ \dot{y}_1(0) = 0\\ \ddot{y}_1(t) = -g \end{array} \right\} \Longrightarrow \left\{ \begin{array}{l} \dot{y}_1(t) = -gt\\ y_1(t) = h-gt^2/2 \end{array} \right.$

Entonces los vectores de posición y velocidad de la partícula 1 es

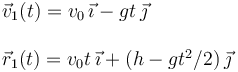
$\begin{array}{l} \vec{v}_1(t) = v_0\,\vec{\imath} -gt\,\vec{\jmath}\\ \\ \vec{r}_1(t) = v_0t\,\vec{\imath} + (h-gt^2/2)\,\vec{\jmath} \end{array}$

La partícula 2 realiza un movimiento rectilíneo en el que la aceleración es una función del tiempo. Tenemos que resolver la ecuación diferencial. La aceleración de la partícula 2 sobre el eje $O X$ es

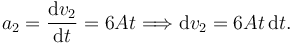
$a_2 = \dfrac{\mathrm{d}v_2}{\mathrm{d}t} = 6At \Longrightarrow \mathrm{d}v_2 = 6At\,\mathrm{d}t.$

Podemos integrar esta expresión

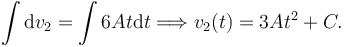
$\int \mathrm{d}v_2 = \int 6At\mathrm{d}t \Longrightarrow v_2(t) = 3At^2 + C.$

La constante de integración se calcula imponiendo la condición inicial para la velocidad de la partícula 2

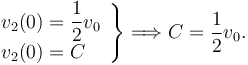
$\left. \begin{array}{l} v_2(0) = \dfrac{1}{2}v_0\\ v_2(0) = C \end{array} \right\} \Longrightarrow C=\dfrac{1}{2}v_0.$

Por tanto, la velocidad de la partícula 2 es

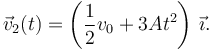
$\vec{v}_2(t) = \left(\dfrac{1}{2}v_0 + 3At^2\right)\,\vec{\imath}.$

Procedemos de manera similar para encontrar $x 2 (t)$

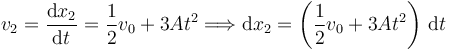
$v_2 = \dfrac{\mathrm{d}x_2}{\mathrm{d}t} = \dfrac{1}{2}v_0 + 3At^2 \Longrightarrow \mathrm{d}x_2 = \left(\dfrac{1}{2}v_0 + 3At^2\right)\,\mathrm{d}t$

Podemos integrar esta expresión

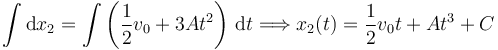
$\int \mathrm{d}x_2 = \int \left(\dfrac{1}{2}v_0 + 3At^2\right)\,\mathrm{d}t \Longrightarrow x_2(t) = \dfrac{1}{2}v_0t + At^3 + C$

La constante de integración se calcula imponiendo la condición inicial para la posición de la partícula 2

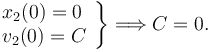
$\left. \begin{array}{l} x_2(0) = 0\\ v_2(0) = C \end{array} \right\} \Longrightarrow C=0.$

Por tanto, el vector de posición de la partícula 2 es

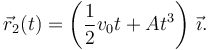
$\vec{r}_2(t) = \left(\dfrac{1}{2}v_0t + At^3\right)\,\vec{\imath}.$

2.2 Colisión de las partículas

Para que las partículas colisionen sus dos vectores de posición tienen que ser iguales en el instante de la colisión, $t = t c$

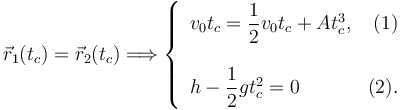
$\vec{r}_1(t_c) = \vec{r}_2(t_c) \Longrightarrow \left\{ \begin{array}{lr} v_0t_c = \dfrac{1}{2}v_0t_c + At_c^3, & (1)\\ \\ h-\dfrac{1}{2}gt_c^2 = 0 & (2). \end{array} \right.$

A partir de la ecuación (2) obtenemos

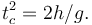
$t_c^2 = 2h/g.$

En la ecuación (1) podemos eliminar una $t c$ en todos los sumandos. Despejando el valor de $v 0$ tenemos

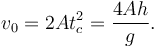
$v_0 = 2At_c^2 = \dfrac{4Ah}{g}.$

2.3 Vector tangente de la partícula 1 en el instante de la colisión

El vector velocidad de la partícula 1 cuando colisionan, 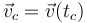$\vec{v}_c=\vec{v}(t_c)$ , es

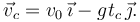
$\vec{v}_c = v_0\,\vec{\imath} -gt_c\,\vec{\jmath}.$

Sustituyendo los valores de $v 0$ y $t c$ calculados en la pregunta anterior, y aplicando la condición 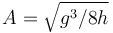$A=\sqrt{g^3/8h}$ tenemos

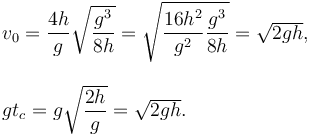
$\begin{array}{l} v_0 = \dfrac{4h}{g}\sqrt{\dfrac{g^3}{8h}} = \sqrt{\dfrac{16h^2}{g^2}\dfrac{g^3}{8h}} = \sqrt{2gh},\\ \\ gt_c = g\sqrt{\dfrac{2h}{g}} = \sqrt{2gh}. \end{array}$

Por tanto la velocidad en ese instante, así como su módulo son

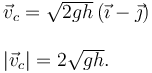
$\begin{array}{l} \vec{v}_c = \sqrt{2gh}\,(\vec{\imath} - \vec{\jmath})\\ \\ |\vec{v}_c| = 2\sqrt{gh}. \end{array}$

Por lo que el vector tangente en ese instante es

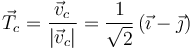
$\vec{T}_c = \dfrac{\vec{v}_c}{|\vec{v}_c|} = \dfrac{1}{\sqrt{2}}\,(\vec{\imath} - \vec{\jmath})$

Otra forma de ver que, de todas las opciones que se daban para responder, esta es la única con la dirección correcta teniendo en cuenta la trayectoria de la partícula 1. El vector tangente tiene que apuntar hacia la derecha y hacia abajo.

Partículas en colisión, Noviembre 2018 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimientos de las partículas

2.2 Colisión de las partículas

2.3 Vector tangente de la partícula 1 en el instante de la colisión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES