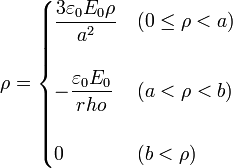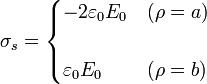Campo eléctrico con simetría cilíndrica
De Laplace
Revisión a fecha de 11:24 25 ene 2009; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Un campo eléctrico con simetría cilíndrica está definido por la siguiente expresión, expresada en coordenadas cilíndricas:
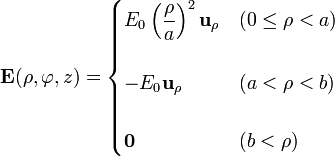
- Determine las distribuciones de carga que producen este campo eléctrico, así como la carga eléctrica total.
- Obtenga la expresión del potencial electrostático creado por esas distribuciones.
- Halle la energía electrostática almacenada entre dos planos z = 0 y z = h.
2 Solución
2.1 Distribuciones de carga
En este sistema podemos tener distribuciones de carga de volumen y de superficie.
2.1.1 Distribución volumétrica
La densidad de carga de volumen, ρ, la podemos calcular aplicando la ley de Gauss en forma diferencial
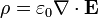
Tenemos tres regiones, en cada una de las cuales la densidad tiene una expresión diferente
- Para 0 < ρ < a, calculamos la divergencia empleando coordenadas cilíndricas

- Para a < ρ < b, empleando el mismo procedimiento
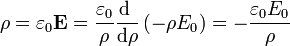
- Para b < ρ el campo es nulo, y su divergencia, también
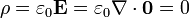
2.1.2 Distribución superficial
Además de las cargas en el volumen, podemos tener densidades superficiales de carga en las superficies en que el campo sea discontinuo. Esta densidad la da el salto en las componentes normales del campo eléctrico
![\sigma_s = \varepsilon_0\mathbf{n}\cdot[\mathbf{E}]](/wiki/images/math/7/0/1/701cf1e1b2222fb5d82be7033b3ca174.png)
Tenemos dos posibilidades
- En ρ = a, el vector normal es
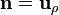 , y la densidad de carga
, y la densidad de carga
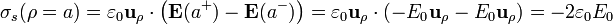
- En ρ = b, operando del mismo modo,

Reuniendo todos los resultados, tenemos las densidades de carga