Introducción a la dinámica del sólido rígido (GIE)
De Laplace
Introducción
El sólido rígido sirve como modelo de sólidos reales sometidos a fuerzas moderadas, que producen una deformación despreciable.
Tal como se describe en el tema de cinemática del sólido rígido, en este modelo, el sólido se puede considerar como formado por un conjunto de partículas que satisfacen la condición (geométrica y cinemática) de rigidez. Esta condición implica, a su vez, que la velocidad de las diferentes partículas no puede ser arbitraria, sino que deben estar relacionadas por el teorema de Chasles

o, usando el vector de posición relativa
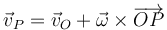
Esta ecuación (o la condición, equivalente, de rigidez) implica que un sólido rígido posee 6 grados de libertad, correspondientes a determinar las tres componentes de la velocidad del origen 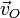 y la velocidad angular
y la velocidad angular  .
.
Por ello, el estudio de la dinámica del sólido rígido consiste en establecer, y resolver si es posible, las ecuaciones de evolución para estas dos velocidades a partir del conocimiento de las fuerzas aplicadas sobre el sólido. En este sentido, las ecuaciones de la dinámica del sólido rígido constituyen una particularización de las ecuaciones de la dinámica de un sistema de partículas, que para este caso se reducen a dos ecuaciones vectoriales.
Como en el caso de la dinámica de la partícula, los sólidos pueden estar sometidos a vínculos o ligaduras, que introducen limitaciones en los movimientos posibles (un ejemplo de esto lo constituyen los diferentes pares cinemáticos vistos en en el tema correspondiente). Estos vínculos llevan asociados fuerzas y momentos de reacción vincular como incógnitas adicionales del problema.
El estudio de la dinámica del sólido rígido puede ser extremadamente complicado. En esta introducción al tema consideraremos solo las propiedades más simples y los casos más sencillos.
Para organizar el tema, estructuraremos su contenido en las siguientes secciones:





