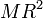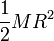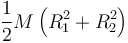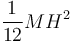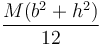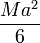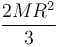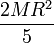Propiedades dinámicas de un sólido rígido

De Laplace

Contenido

1 Introducción
2 Masa
3 Centro de masas
4 Cantidad de movimiento
5 Momento cinético
6 Momento de inercia
7 Energía cinética
8 Energía potencial

1 Introducción

A la hora de establecer las ecuaciones de la dinámica del sólido rígido se debe, en primer lugar, definir qué magnitudes lo caracterizan, para poder escribir correctamente las ecuaciones de evolución.

2 Masa

En cinemática del sólido rígido no es necesario considerar la extensión real del sólido. Puede describirse el campo de velocidades suponiendo que se extiende a todos los puntos del espacio tanto interiores como exteriores al sólido, sin importar si en estos puntos existe una partícula material o no.

En dinámica, en cambio, sí es importante considerar la extensión finita del sólido. Un sólido real ocupa un volumen $V$ que por definición es indeformable (aunque puede trasladarse y rotar en el espacio). En este volumen existe una serie de partículas, con masas $m i$ de forma que el sólido posee una masa total

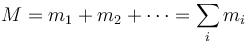
$M = m_1+m_2+\cdots = \sum_i m_i$

Para la mayoría de los sólidos, no obstante, es preferible modelarlos como un continuo que llena toda una región del espacio. En cada elemento de volumen $d V$ existe una pequeña cantidad de sólido relacionada con el volumen a través de la densidad de masa

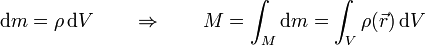
$\mathrm{d}m = \rho\,\mathrm{d}V\qquad\Rightarrow\qquad M = \int_M \mathrm{d}m = \int_V \rho(\vec{r})\,\mathrm{d}V$

En un sólido homogéneo la densidad de masa es la misma en todos sus puntos y

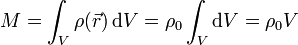
$M = \int_V \rho(\vec{r})\,\mathrm{d}V = \rho_0\int_V\mathrm{d}V = \rho_0V$

Así para sólidos homogéneos de formas:

Prisma rectangular:

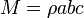
$M = \rho abc\,$

Cilindro

$M = \pi\rho R^2 h\,$

Esfera

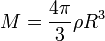
$M = \frac{4\pi}{3}\rho R^3\,$

En ocasiones puede suponerse que un sólido se reduce a una fina lámina. Se define entonces la densidad superficial de masa, $σ$ ,

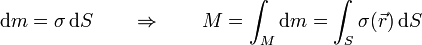
$\mathrm{d}m = \sigma\,\mathrm{d}S\qquad\Rightarrow\qquad M = \int_M \mathrm{d}m = \int_S \sigma(\vec{r})\,\mathrm{d}S$

que, para el caso de un sólido homogéneo nos da

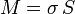
$M = \sigma\,S$

Así, por ejemplo, para una hoja tamaño A4 de 80 g/m² su masa es

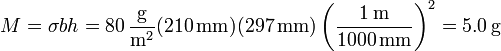
$M = \sigma b h = 80\,\frac{\mathrm{g}}{\mathrm{m}^2}(210\,\mathrm{mm})(297\,\mathrm{mm})\left(\frac{1\,\mathrm{m}}{1000\,\mathrm{mm}}\right)^2 = 5.0\,\mathrm{g}$

Aplicando las fórmulas del área de una superficie cilíndrica o esférica obtenemos las masas

$M = 2\pi\sigma\,R\,h\quad\mbox{(cilindro)}\qquad\qquad M = 4\pi\sigma R^2\quad\mbox{(esfera)}$

Análogamente, existen sólidos que pueden suponerse lineales (como un alambre o varilla), en cuyo caso se define la densidad lineal de masa, $μ$

$\mathrm{d}m=\mu\,\mathrm{d}l\qquad\qquad M = \int_L \mu\,\mathrm{d}l$

3 Centro de masas

Como con cualquier otro sistema de partículas, un sólido rígido se caracteriza por tener un centro de masas cuya posición es una media ponderada de las posiciones de las partículas que lo componen

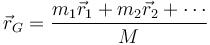
$\vec{r}_G = \frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{M}$

En el caso de una distribución continua, el sumatorio se sustituye por una integral

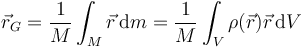
$\vec{r}_G = \frac{1}{M}\int_M \vec{r}\,\mathrm{d}m = \frac{1}{M}\int_V\rho(\vec{r})\vec{r}\,\mathrm{d}V$

A la hora de localizar el centro de masas de un sólido es importante hacer uso de las simetrías del sólido:

Si el sólido es simétrico respecto a un determinado plano, el CM se encuentra contenido en el plano de simetría.
Si el sólido es simétrico respecto a dos o más planos, el CM se encuentra en la intersección de los distintos planos de simetría.
Si el sólido es una figura de revolución en torno a un eje dado, el CM se halla sobre el eje de revolución.

4 Cantidad de movimiento

La cantidad de movimiento de un sólido es igual a la suma de la cantidad de movimiento de cada una de las partículas que lo componen

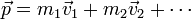
$\vec{p}=m_1\vec{v}_1+m_2\vec{v}_2+\cdots$

Por tratarse de un sólido, estas velocidades verifican el teorema de Chasles

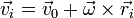
$\vec{v}_i = \vec{v}_0+\vec{\omega}\times\vec{r}_i$

lo cual, al sustituir en la expresión de la cantidad de movimiento, nos da

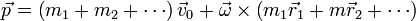
$\vec{p}=\left(m_1+m_2+\cdots\right)\vec{v}_0+\vec{\omega}\times\left(m_1\vec{r}_1+m\vec{r}_2+\cdots\right)$

El primero de los dos paréntesis es la masa total del sólido, mientras que el segundo nos da la posición del centro de masas

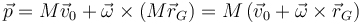
$\vec{p}=M\vec{v}_0+\vec{\omega}\times\left(M\vec{r}_G\right)=M\left(\vec{v}_0+\vec{\omega}\times\vec{r}_G\right)$

Por otro lado, la cantidad de movimiento de un sistema de partículas se relaciona con la velocidad del centro de masas

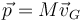
$\vec{p}=M\vec{v}_G$

Igualando ambas expresiones obtenemos la velocidad del centro de masas del sólido

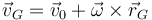
$\vec{v}_G = \vec{v}_0+\vec{\omega}\times\vec{r}_G$

Esta igualdad simplemente nos dice que el centro de masas se mueve rígidamente con el sólido estando siempre en la misma posición relativa a éste (aunque el CM puede no coincidir con ninguna de las partículas del sólido, se mueve como una más de ellas).

5 Momento cinético

El momento cinético del sólido equivale a la suma de los momentos cinéticos de cada una de las partículas que lo componen

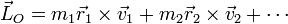
$\vec{L}_O=m_1\vec{r}_1\times\vec{v}_1+m_2\vec{r}_2\times\vec{v}_2 + \cdots$

Este momento cinético puede descomponerse en una parte debida al movimiento con el centro de masas más otra debida al movimiento alrededor del centro de masas

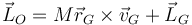
$\vec{L}_O=M\vec{r}_G\times\vec{v}_G + \vec{L}_G$

siendo

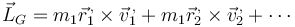
$\vec{L}_G = m_1\vec{r}^{\,,}_1\times\vec{v}^{\,,}_1+m_1\vec{r}^{\,,}_2\times\vec{v}^{\,,}_2 + \cdots$

Si aquí sustituimos la expresión del campo de velocidades de un sólido,

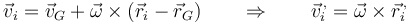
$\vec{v}_i = \vec{v}_G + \vec{\omega}\times(\vec{r}_i-\vec{r}_G)\qquad\Rightarrow\qquad \vec{v}^{\,,}_i=\vec{\omega}\times\vec{r}_i^{\,,}$

nos queda

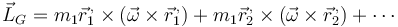
$\vec{L}_G = m_1\vec{r}^{\,,}_1\times(\vec{\omega}\times\vec{r}_1^{\,,})+m_1\vec{r}^{\,,}_2\times(\vec{\omega}\times\vec{r}_2^{\,,}) + \cdots$

Debido al doble producto vectorial, esta expresión es bastante más compleja que la de la cantidad de movimiento, por lo que solo consideraremos los casos más sencillos.

Supongamos una partícula $m 1$ que describe una circunferencia de radio $R 1$ en torno al CM con velocidad angular $\vec{\omega}$ . El momento cinético de esta partícula respecto al centro de la circunferencia es perpendicular al plano de ésta y de módulo

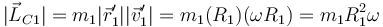
$|\vec{L}_{C1}| = m_1|\vec{r}'_1||\vec{v}'_1| = m_1(R_1)(\omega R_1) = m_1R_1^2\omega$

Puesto que en este caso el momento cinético tiene la misma dirección y sentido que la velocidad angular, podemos escribir esta expresión en forma vectorial

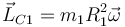
$\vec{L}_{C1} = m_1R_1^2\vec{\omega}$

Si ahora consideramos un sólido simétrico (como un disco, una esfera o un cilindro) que gira en torno un eje dado que pasa por el CM, cada uno de los puntos contribuye de manera análoga y el momento cinético total respecto al CM vale

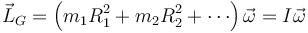
$\vec{L}_G=\left(m_1R_1^2+m_2R_2^2+\cdots\right)\vec{\omega}=I\vec{\omega}$

siendo $R i$ la distancia de cada punto al eje e $I$ una nueva magnitud conocida como momento de inercia (que se discute con más detalle más adelante).

Esta igualdad nos dice que el momento cinético de un sólido simétrico respecto a un eje que pasa por su CM es proporcional a la velocidad angular con la que gira, de manera análoga a cómo la cantidad de movimiento es proporcional a la velocidad del CM. La constante de proporcionalidad es el momento de inercia, que desempeña el papel de la masa en cuanto a medida de la inercia del sólido respecto a una rotación.

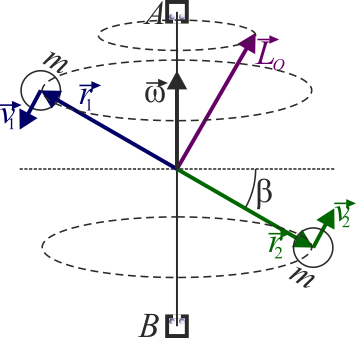
La igualdad anterior no siempre es cierta, ya que para una partícula el momento cinético respecto a un punto que no es el centro de la circunferencia que describe (aunque sea del eje de rotación) no será en general paralelo a la velocidad angular. Sólo para sólidos que tienen este eje como de simetría se cancelan las componentes no paralelas y resulta una situación de paralelismo entre $\vec{L}_G$ y $\vec{\omega}$ . Un ejemplo sencillo donde el momento cinético no es paralelo a la velocidad angular es el de un rotor desequilibrado.

6 Momento de inercia

6.1 Definición

Dado un sólido rígido, se define su momento de inercia respecto a un eje como la cantidad

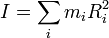
$I = \sum_i m_i R_i^2\,$

donde $R i$ es la distancia de una partícula $m 1$ al eje. En el caso de que tengamos una distribución continua, la expresión correspondiente es la integral

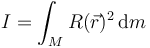
$I = \int_M R(\vec{r})^2\,\mathrm{d}m$

donde $R$ será en general diferente para cada elemento de masa $d m$ .

De la definición del momento de inercia se deduce que sus dimensiones son de una masa por una longitud al cuadrado y sus unidades en el SI son kg·m²

En los casos particulares frecuentes de que el eje respecto al que se calcula el momento de inercia se haga coincidir con uno de los ejes de coordenadas obtenemos los momentos de inercia

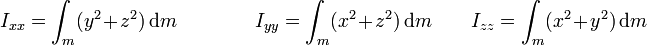
$I_{xx}=\int_m(y^2+z^2)\,\mathrm{d}m\qquad\qquad I_{yy}=\int_m(x^2+z^2)\,\mathrm{d}m\qquad I_{zz}=\int_m(x^2+y^2)\,\mathrm{d}m$

6.2 Ejemplos elementales

Rotor equilibrado: Consideremos un rotor formado por dos masas iguales de valor $m$ situadas en los extremos de una varilla rígida ideal (sin masa) de longitud $H$ con un eje de giro perpendicular a ella y que pasa por su centro. La distancia de cada masa al eje es la mitad de la longitud de la varilla, por lo que

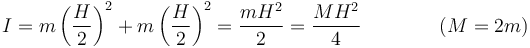
$I = m\left(\frac{H}{2}\right)^2 +m\left(\frac{H}{2}\right)^2 = \frac{mH^2}{2}=\frac{MH^2}{4}\qquad\qquad (M = 2m)$

Varilla homogénea: Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro

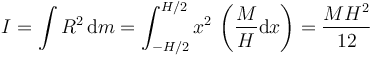
$I = \int R^2\,\mathrm{d}m=\int_{-H/2}^{H/2} x^2\,\left(\frac{M}{H}\mathrm{d}x\right)=\frac{MH^2}{12}$

donde hemos aplicado que por ser homogénea

$\mathrm{d}m=\mu\,\mathrm{d}x\qquad\qquad\mu = \frac{M}{L}$

Superficie cilíndrica: Para una superficie cilíndrica de radio $R$ y altura $h$ , el momento de inercia respecto al eje del cilindro es, simplemente

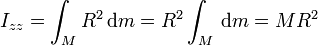
$I_{zz}=\int_M R^2\,\mathrm{d}m = R^2\int_M\,\mathrm{d}m = MR^2$

ya que todos los puntos se encuentran a la misma distancia del eje.

Cilindro macizo: Si en cambio consideramos un cilindro macizo homogéneo de radio $R$ y altura $h$ , su momento de inercia es igual a

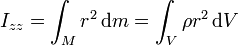
$I_{zz}=\int_M r^2\,\mathrm{d}m = \int_V \rho r^2\,\mathrm{d}V$

Como elementos de volumen consideramos finas películas cilíndricas de radio

r

y espesor

d r

, cada una de las cuales tiene el volumen diferencial

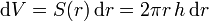
$\mathrm{d}V = S(r)\,\mathrm{d}r = 2\pi r\,h\,\mathrm{d}r$

Llevando esto al momento de inercia nos queda

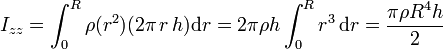
$I_{zz} = \int_0^R \rho(r^2)(2\pi\,r\,h)\mathrm{d}r = 2\pi\rho h\int_0^R r^3\,\mathrm{d}r=\frac{\pi \rho R^4 h}{2}$

Vemos que para cilindros del mismo material (con la misma densidad de masa), el momento de inercia va como la cuarta potencia del radio (esto es, doble de radio significa que el momento de inercia se multiplica por 16). Sustituyendo el valor de la densidad de masa

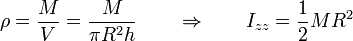
$\rho = \frac{M}{V}=\frac{M}{\pi R^2 h}\qquad\Rightarrow\qquad I_{zz}=\frac{1}{2}MR^2$

El momento de inercia de un cilindro macizo es entonces la mitad del de una superficie cilíndrica de la misma masa y el mismo radio.

Puesto que estos resultados no dependen de la altura del cilindro también son aplicables al caso de un anillo (superficie cilíndrica de altura muy pequeña) y de un disco (cilindro macizo de muy pequeño espesor).

6.3 Teorema de Steiner (o de los ejes paralelos)

El momento de inercia puede definirse respecto a un eje arbitrario, que no necesariamente debe pasar por el centro de masas del sólido. No obstante, los ejes que pasan por el CM tienen propiedades particulares.

Consideremos dos ejes paralelos: uno que pasa por el CM y uno situado a una distancia $d$ del primero. Sea $I G$ el momento de inercia respecto al eje que pasa por el CM e $I$ el momento de inercia respecto al eje paralelo. Buscamos una relación entre estas dos cantidades.

Si consideramos el eje Z como el paralelo al que pasa por el CM el momento de inercia se puede escribir

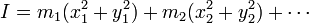
$I = m_1(x_1^2+y_1^2) + m_2(x_2^2+y_2^2)+\cdots$

Introduciendo las posiciones relativas al CM

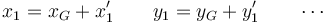
$x_1 = x_G + x_1'\qquad y_1 = y_G + y_1'\qquad \cdots$

queda

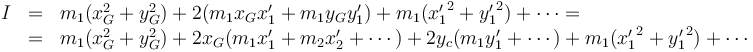
$\begin{array}{rcl} I & = & m_1(x_G^2+y_G^2) + 2(m_1x_Gx'_1 +m_1y_Gy'_1) + m_1({x'_1}^2 +{y'_1}^2)+\cdots = \\ & = & m_1(x_G^2+y_G^2) + 2x_G(m_1x'_1+m_2x'_2+\cdots) +2y_c(m_1y'_1+\cdots) + m_1({x'_1}^2 +{y'_1}^2)+\cdots \end{array}$

Ahora bien, la posición del centro de masas relativa a sí mismo es nula, por lo que

$m_1 x'_1+m_2x'_2 + ... =0\qquad\qquad m_1y'_1+m_2y'_2 + ... =0$

Además se cumple

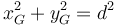
$x_G^2+y_G^2 = d^2\,$

con $d$ la distancia entre los ejes. Llevando esto a la expresión del momento de inercia queda

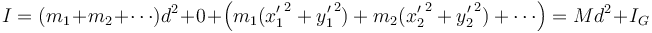
$I = (m_1+m_2+\cdots)d^2 + 0 + \left(m_1({x'_1}^2 +{y'_1}^2)+m_2({x'_2}^2 +{y'_2}^2)+\cdots\right) = Md^2 + I_G$

Este es el teorema de Steiner o de los ejes paralelos. Nos permite calcular el momento de inercia respecto a un eje arbitrario si conocemos el valor respecto a un eje paralelo que pase por el CM.

Este teorema nos dice que el momento de inercia en ejes paralelos es mínimo en el eje que pasa por el CM (lo cual sirve también como definición del centro de masas).

Por ejemplo, consideremos el momento de inercia de una varilla de masa M y longitud H alrededor de un eje que pasa por su extremo.

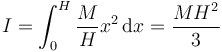
$I= \int_{0}^{H}\frac{M}{H}x^2\,\mathrm{d}x = \frac{MH^2}{3}$

Si hallamos la diferencia con el que calculamos antes para el eje que pasa por el centro

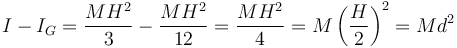
$I - I_G = \frac{MH^2}{3}-\frac{MH^2}{12}= \frac{MH^2}{4}=M\left(\frac{H}{2}\right)^2 = Md^2$

6.4 Teorema de la figura plana (o de los ejes perpendiculares)

Una sólido puede considerarse plano cuando sus dimensiones en una determinada dirección son mucho más pequeñas que a lo largo de las normales a ella. Es el caso, por ejemplo, de una chapa metálica en forma de disco o el de una varilla.

Si consideramos que la coordenada $z$ es la que tiene espesor despreciable, podemos suponer que $z = 0$ para todos los puntos del sólido. Esto deja los tres momentos de inercia respecto a los ejes de coordenadas en

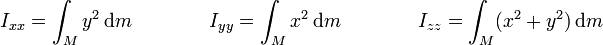
$I_{xx}=\int_M y^2\,\mathrm{d}m\qquad\qquad I_{yy}=\int_M x^2\,\mathrm{d}m \qquad\qquad I_{zz}=\int_M (x^2+y^2)\,\mathrm{d}m$

de donde es inmediato que

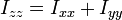
$I_{zz} = I_{xx}+I_{yy}\,$

Esta relación permite calcular uno de los momentos de inercia conocidos los otros dos.

Por ejemplo, si deseamos hallar el momento de inercia de un disco circular respecto a un eje diametral podemos aplicar que, por simetría y por el teorema de la figura plana

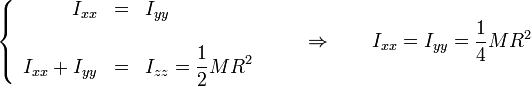
$\left\{\begin{array}{rcl}I_{xx} &= & I_{yy} \\ && \\ I_{xx}+I_{yy} &= & I_{zz}=\displaystyle\frac{1}{2}MR^2\end{array}\right.\qquad\Rightarrow\qquad I_{xx}=I_{yy}=\frac{1}{4}MR^2$

6.5 Casos particulares

Por su interés, es conveniente tabular casos particulares de momentos de inercia de sólidos homogéneos. Muchos otros pueden hallarse

Sólido	Eje	Momento de inercia
Superficie cilíndrica de radio $R$ y altura $h$	El del cilindro	$MR^2\,$
Cilindro macizo de radio $R$ y altura $h$	El del cilindro	$\frac{1}{2}MR^2$
Cilindro hueco de radio interior $R 1$ , exterior $R 2$ y altura $h$	El del cilindro	$\frac{1}{2}M\left(R_1^2+R_2^2\right)$
Varilla rectilínea de longitud $H$	Perpendicular por el centro	$\frac{1}{12}MH^2$
Paralelogramo de lados $b$ y $h$ (incluye cuadrados, rectángulos y rombos)	Perpendicular por el centro	$\frac{M(b^2+h^2)}{12}$
Cubo macizo de arista $R$	Cualquiera que pase por su centro	$\frac{Ma^2}{6}$
Esfera hueca de radio $R$	Cualquiera que pase por su centro	$\frac{2MR^2}{3}$
Esfera maciza de radio $a$	Cualquiera que pase por su centro	$\frac{2MR^2}{5}$

Vemos que para aquellos que se caracterizan por una sola distancia R (radio, longitud,...), la forma del momento de inercia es

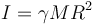
$I=\gamma M R^2\,$

con γ un número que depende del objeto. En particular, para objetos redondos (con R el radio) tenemos

Cuerpo	Cilindro hueco	Cilindro macizo	Esfera hueca	Esfera maciza
$\gamma\,$	$1\,$	$\frac{1}{2}$	$\frac{2}{3}$	$\frac{2}{5}$

Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando.

7 Energía cinética

la energía cinética de un sistema es la suma de las energías cinéticas individuales

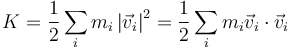
$K = \frac{1}{2}\sum_im_i\left|\vec{v}_i\right|^2=\frac{1}{2}\sum_im_i\vec{v}_i\cdot\vec{v}_i$

Sustituyendo una de las velocidades por la expresión del campo de velocidades respecto un punto O

$K=\frac{1}{2}\sum_i m_i(\vec{v}_O+\vec{\omega}\times\overrightarrow{OP}_i)\cdot\vec{v}_i$

y si aquí sacamos factores comunes

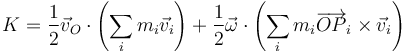
$K = \frac{1}{2}\vec{v}_O\cdot\left(\sum_im_i\vec{v}_i\right)+\frac{1}{2}\vec{\omega}\cdot\left(\sum_i m_i\overrightarrow{OP}_i\times\vec{v}_i\right)$

y aplicando las definiciones de la cantidad de movimiento y del momento cinético

$K = \frac{1}{2}\vec{v}_O\cdot\vec{p}+\frac{1}{2}\vec{\omega}\cdot\vec{L}_O$

Esta relación es independiente del centro de reducción que se tome. En particular, puede ser el centro de masas, ya que

$K = \frac{1}{2}\vec{p}\cdot\left(\vec{v}_G+\vec{\omega}\times\overrightarrow{GO}\right)+\frac{1}{2}\vec{\omega}\cdot\vec{L}_O = \frac{1}{2}\vec{p}\cdot\vec{v}_G+\vec{\omega}\cdot\left(\vec{L}_O+\vec{p}\times\overrightarrow{OG}\right)=\frac{1}{2}\vec{v}_G\cdot\vec{p}+\frac{1}{2}\vec{\omega}\cdot\vec{L}_G$

La relación

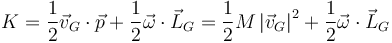
$K=\frac{1}{2}\vec{v}_G\cdot\vec{p}+\frac{1}{2}\vec{\omega}\cdot\vec{L}_G=\frac{1}{2}M\left|\vec{v}_G\right|^2+\frac{1}{2}\vec{\omega}\cdot\vec{L}_G$

es un caso particular de la descomposición de la energía cinética en dos partes:

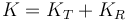
$K = K_T+K_R\,$

Una energía cinética de traslación, que sería la que tendría el sólido si todo él se moviera como el centro de masas

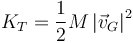
$K_T=\frac{1}{2}M\left|\vec{v}_G\right|^2$

Una energía cinética de movimiento alrededor del centro de masas, que en el caso de un sólido sólo puede ser energía cinética de rotación (ya que no hay deformaciones)

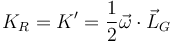
$K_R = K'=\frac{1}{2}\vec{\omega}\cdot\vec{L}_G$

En el caso particular de un sólido que gira en torno a un eje tal que el momento cinético es paralelo a la velocidad angular, esto se reduce a

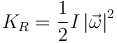
$K_R=\frac{1}{2}I\left|\vec{\omega}\right|^2$

8 Energía potencial

En un sistema de partículas libres, el concepto de energía potencial es difícil de definir, ya que debe tener en cuenta la energía debida a las interacciones entre las partículas del sistema (por ejemplo, la energía eléctrica debida a la presencia de partículas cargadas), y esta es dependiente de las posiciones relativas de las partículas.

En un sólido rígido, en cambio, al ser fijas las distancias entre partículas, la energía de interacción interna permanece constante y no interviene en la dinámica del sistema. Por ello, podemos restringirnos a usar la energía potencial debida a fuerzas externas (la causada por el campo gravitatorio, por un campo eléctrico aplicado, etc.).

La energía potencial total del sólido será la suma de las de las partículas que lo componen

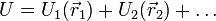
$U = U_1(\vec{r}_1) + U_2(\vec{r}_2)+\ldots$

En el caso general, este cálculo puede ser extremadamente complicado y requerir información que no está disponible. Por ejemplo, para la energía potencial eléctrica no nos basta con saber la masa y forma del sólido: debemos conocer dónde se encuentran las cargas del sistema y cuánto vale cada una.

Un caso en el que sí se pueden hacer los cálculos correspondientes es el de la energía potencial debida al peso.

Suponiendo que la aceleración de la gravedad se expresa en la forma habitual

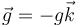
$\vec{g}=-g\vec{k}$

la energía potencial de cada una de las masas es de la forma $U i = m i g z i$ con la altura medida respecto a un nivel de referencia (el mismo para todas las partículas). Esto nos da una energía potencial total

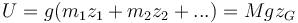
$U = g(m_1z_1+m_2z_2+...) = Mgz_G\,$

esto es, equivale al que tendría una partícula con la masa total del sistema situada a la altura del centro de masas. Puesto que esto debe ser cierto sea cual sea la orientación del sólido (esto es, si giramos el sólido 90° se obtiene lo mismo pero con $x G$ o $y G$ ), se puede concretar más y decir que la energía potencial gravitatoria es la misma que tendría si toda la masa estuviera concentrada en la posición del centro de masas. Esta es una de las razones por las que al centro de masas se le denomina también centro de gravedad. Hay que destacar, no obstante, que esta relación deja de cumplirse si el campo gravitatorio depende de la posición (el centro de gravedad de la Luna no coincide con el centro de masas, ya que la atracción terrestre no es la misma en todos sus puntos).

Propiedades dinámicas de un sólido rígido

De Laplace

Contenido

1 Introducción

2 Masa

3 Centro de masas

4 Cantidad de movimiento

5 Momento cinético

6 Momento de inercia

6.1 Definición

6.2 Ejemplos elementales

6.3 Teorema de Steiner (o de los ejes paralelos)

6.4 Teorema de la figura plana (o de los ejes perpendiculares)

6.5 Casos particulares

7 Energía cinética

8 Energía potencial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES